德州市高中三年级教学质量检测
数学试题(文科) 2006年3月
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟.
第Ⅰ卷(选择题共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上;
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净,再选涂其它答案.不能答在试卷上;
3.考试结束,将第Ⅱ卷和答题卡一并交回.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率:
Pn(k)=CknPk(1-P)n-k
球的体积公式:V=43πR3(其中R表示球的半径)
球的表面积公式:S=4πR2(其中R表示球的半径)
一、选择题(本大题共12小题,每小题5分,共计60分.在每小题列出的四个选项中,只有一项是符合题目要求的.)
1.已知集合![]() ,那么
,那么![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() ,(x∈R),则
,(x∈R),则![]()
A
0 B
3.在![]() ABC中,若cosAcosB>sinAsinB,则方程x2cosA+y2cosC=1表示
ABC中,若cosAcosB>sinAsinB,则方程x2cosA+y2cosC=1表示
A 焦点在x轴上的椭圆 B焦点在y轴上的椭圆
 C 焦点在x轴上的双曲线 D焦点在y轴上的双曲线
y
C 焦点在x轴上的双曲线 D焦点在y轴上的双曲线
y
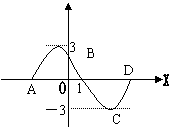
4.y=f(x)是以2![]() 为周期的周期函数,其图象的一部分
为周期的周期函数,其图象的一部分
如图所示,则y=f(x)的解析式是( )
![]()
![]()
![]() A.y=3sin(x+1) B.y=-3sin(x+1)
A.y=3sin(x+1) B.y=-3sin(x+1)
![]() C.y=3sin(x-1) D.y=-3sin(x-1)
C.y=3sin(x-1) D.y=-3sin(x-1)
5. 在等差数列![]() 中,若
中,若![]() ,则
,则![]() 的值为( )
的值为( )
A.14
B.
6.已知椭圆![]() (a>b>0)的左焦点是F,A、B分别是左顶点和上顶点 ,若F到直线AB的距离是
(a>b>0)的左焦点是F,A、B分别是左顶点和上顶点 ,若F到直线AB的距离是![]() ,则椭圆的离心率是( )
,则椭圆的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 在R上定义运算*:x*y=![]() ,若关于x的不等式(x-a)*(x+1-a)>0的解集是集合{x-1≤x≤1,x∈R} 的子集,则实数a的取值范围是
,若关于x的不等式(x-a)*(x+1-a)>0的解集是集合{x-1≤x≤1,x∈R} 的子集,则实数a的取值范围是
A.-1≤a≤1 B.0≤a≤
8.二项式(1-x)4n+1(![]() )的展开式中系数最大的项为( )
)的展开式中系数最大的项为( )
A.第2n+1项或2n+2项 B.第2n+1项
C.第2n+2项 D.第2n或2n+1项
9.某地区对用户用电推出两种收费办法,供用户选择使用:一是按固定电价收取;二是按分时电价收取,即在固定电价的基础上,平时时段电价每千瓦时上浮0.03元;低谷时段电价每千瓦时下浮0.25元.若一用户某月平时时段用电140千瓦时,低谷时段用电60千瓦时,则相对于固定电价收费该月该用户
A.多付电费10.8元 B.少付电费10.8元 C.少付电费15元 D.多付电费4.2元
10.已知![]() 为原点,点
为原点,点![]() (x,y)在单位圆x2+y2=1上,点
(x,y)在单位圆x2+y2=1上,点![]() (2cos
(2cos![]() ,2sin
,2sin![]() )且
)且![]() =(
=(![]() ),则
),则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
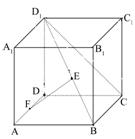
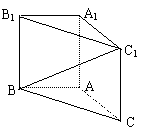 11.在斜三棱柱ABC-A1B
11.在斜三棱柱ABC-A1B
过C1作C1H⊥面ABC,垂足为H,则( )
A.H在直线AC上 B.H在直线AB上
C.H在直线BC上 D.H在△ABC内
12.如图电路中4个开关闭合的概率都是0.6,
且相互独立,则灯亮的概率为( )
A.0.8976 B.0.8624
C.0.9744 D.0.7696
二、填空题(每题4分,共16分)
13. 一质点在直角坐标平面上沿直线匀速行进,上午7时和9时该动点的坐标依次为![]() 和
和![]() ,则下午5时该点的坐标是____________ 。
,则下午5时该点的坐标是____________ 。
14.在算式“9×□+1×△=
15.已知约束条件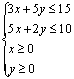 的可行域为D, 将一枚骰子连投两次,设第一次得到的点数为x,第二次得到的点数为y,则点(x, y)落在可行域D内的概率为______________.
的可行域为D, 将一枚骰子连投两次,设第一次得到的点数为x,第二次得到的点数为y,则点(x, y)落在可行域D内的概率为______________.
16.下面四个命题:
①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
②“直线![]() ⊥平面
⊥平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() ⊥平面
⊥平面![]() ”;
”;
③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;
④“平面![]() ∥平面
∥平面![]() ”的必要不充分条件是“
”的必要不充分条件是“![]() 内存在不共线三点到
内存在不共线三点到![]() 的距离相等”;
的距离相等”;
其中正确命题的序号是________________
三、解答题(本大题共6个小题,满分74分.解答应写出文字说明、证明过程或演算步骤.)
17.已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求f(x)的单调增区间.
(2)当![]() 时,求f(x)的最值及此时的x值.
时,求f(x)的最值及此时的x值.
18. 据统计,某大型商场一个结算窗口每天排队的人数及相应的概率如下:
| 排队人数 | [0, 5] | [6,10] | [11,15] | [16,20] | [21,25] | [26,+ |
| 概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)每天不超过20人排队结算的概率是多少?
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
|
(1)建立适当的坐标系,求点E的坐标;
(2)证明:EF![]() 面D1BC;
面D1BC;
(3)求二面角D1-BF-C的余弦值。
20.已知数列![]() 的前n项之和
的前n项之和![]() .求:
.求:
(1)写出数列{an},{bn}的表达式;
(2)求和![]()
21.已知![]() ,
,![]() ,其中O是坐标原点,直线
,其中O是坐标原点,直线![]() 过定点A,其方向向量
过定点A,其方向向量![]() ,动点P到直线
,动点P到直线![]() 的距离为
的距离为![]() ,且
,且![]() =
=![]() .
.
(1) 求动点P的轨迹方程;
(2)
直线m:![]() 与点P的轨迹相交于M,N两个不同点,当
与点P的轨迹相交于M,N两个不同点,当![]() 时,求直线m的倾斜角α的取值范围;
时,求直线m的倾斜角α的取值范围;
22.已知![]() 函数
函数![]() 的图像与函数
的图像与函数![]() 的图象相切.
的图象相切.
(1)求b与c的关系式(用c表示b);
(2)设函数![]() ,
,
(ⅰ)当![]() 时,在函数
时,在函数![]() 的图像上是否存在点
的图像上是否存在点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(ⅱ)若函数![]() 在
在![]() 内有极值点,求c的取值范围.
内有极值点,求c的取值范围.
文科答案
1.D2.A3.C4.D5.C6.C7.C8.B9.B10.A11.B12.A
13.![]() 14.(3,9) 15.
14.(3,9) 15.![]() 16.(2)(4)
16.(2)(4)
17.解:![]()
![]()
=![]() (4分)
(4分)
(1)由![]()
解得![]()
∴单调增区间为![]() (
(![]() ∈Z)(8分)
∈Z)(8分)
(漏掉![]() 扣1分)
扣1分)
(2)∵![]()
![]()
![]() 此时
此时![]()
![]() 此时
此时![]() (12分)
(12分)
![]()
18.解:
(1)每天不超过20人排队结算的概率为:
P=0.1+0.15+0.25+0.25=0.75
答:不超过20人排队结算的概率是0.75(2分)
(2)每天超过15排队结算的概率为0.25+0.2+0.05=0.5(4分)
一周7天中,没有出现超过15排队结算的概率为![]() (6分)
(6分)
一周7天中,有一天出现超过15排队结算的概率为![]() (8分)
(8分)
一周7天中,有两天出现超过15排队结算的概率为![]() (10分)
(10分)
所以有3天或3天以上出现超过15人排队结算的概率为
1-[![]() +
+![]() +
+![]() ]=
]=![]()
所以该商场需要增加结算窗口(12分)
19(1)如图建立空间直角坐标系,设DD1=a,则D(0,0,0),D1(0,0,a),C(0,2,0),B(2,2,0)
![]() ,则
,则![]() ,
,![]() ,由
,由![]() 得
得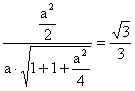 ,解得a=2,故点E的坐标为(1,1,1)(4分)
,解得a=2,故点E的坐标为(1,1,1)(4分)
(2)由(1)知:![]() ,
,![]() ,
,![]()
又![]()
![]() =2-2=0,
=2-2=0,![]()
![]() =0
=0
![]()
![]()
![]() ,
,![]()
![]()
又D1B![]() BC=B,
BC=B,![]() EF
EF![]() 面D1BC(8分)
面D1BC(8分)
(3)由D向BF的延长线作垂线,垂足为M,连结D![]() BF
BF
则![]() 为二面角D1-FB-C的平面角
为二面角D1-FB-C的平面角
在![]() 中,BF=
中,BF=![]() ,又
,又![]()
![]() ,所以
,所以![]()
![]() ,在
,在![]() 中,tan
中,tan![]() =
=![]()
![]() cos
cos![]() =
=![]() ,故二面角D1-FB-C的平面角的余弦值为
,故二面角D1-FB-C的平面角的余弦值为![]() (12分)
(12分)
20. (1)![]() (1分)
(1分)
n≥2时an=Sn-Sn-1=2n-1,
当n=1时,a1=1也应满足an=2n-1,
an=2n-1, (n∈N*).
又![]() 所以bn=n-1(4分)
所以bn=n-1(4分)
(2)n=2k时(k∈N*),![]()
=-(b1+b2+…+b2k)=-[1+2+…+(2k-1)] =-2k2+k (7分)
n=2k-1时(k∈N*), Tn=![]()
=-[1+2+…+(2k-3)] =-2k2-3k+1, (10分)
![]() (12分)
(12分)
21解:(1)由于![]() ,
,![]() ,O为原点,所以A(-2,0),B(2,0)
,O为原点,所以A(-2,0),B(2,0)
又直线![]() 过定点为A,其方向向量为
过定点为A,其方向向量为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .(1分)
.(1分)
由题意,动点P到定点B的距离和到定直线![]() 的距离相等,所以P的轨迹是以B为焦点,
的距离相等,所以P的轨迹是以B为焦点,![]() 为准线的抛物线,其中
为准线的抛物线,其中![]() ,所以动点P的轨迹方程为
,所以动点P的轨迹方程为![]() .
.
(另解:设动点P(x,y),则由![]() ,
,![]() ,整理得
,整理得![]() -----4分
-----4分
![]() (2)由
(2)由 ![]() ,消去y并整理得
,消去y并整理得![]() .
.
![]()
设![]() ,
,![]() ,则根据韦达定理得
,则根据韦达定理得
![]() ,
,![]() ,其中
,其中![]() (6分)
(6分)
![]()
![]()
![]()
![]()
![]()
![]() -
-
而![]() ∴
∴![]() ,又∵
,又∵![]() >0,∴0<
>0,∴0<![]()
∴0<![]() 即0<tan
即0<tan![]()
![]() 1且
1且![]() .
.
∴0<![]() ,即直线
,即直线![]() 的倾斜角
的倾斜角![]() 的范围是
的范围是![]() (12分)
(12分)
22. (1)依题意,令![]()
![]() (4分)
(4分)
(2)![]()
(ⅰ)当![]() 时,
时,![]() ,
,![]()
![]() ,若存在满足条件的点M,则有:
,若存在满足条件的点M,则有:
![]() ,
,![]() ,即这样的点M存在,且坐标为
,即这样的点M存在,且坐标为![]() (8分)
(8分)
(ⅱ)![]()
令![]() (x)=0,即3x2+4bx+b2+c=0;而
(x)=0,即3x2+4bx+b2+c=0;而![]() =16b2-12(b2+c)=4(b2-
=16b2-12(b2+c)=4(b2-
若![]() =0,则
=0,则![]() (x)=0有两个相等的实根,设为x0,此时
(x)=0有两个相等的实根,设为x0,此时![]() (x)的变化如下:
(x)的变化如下:
| x |
| x0 | ( |
|
| + | 0 | + |
于是![]() 不是函数
不是函数![]() 的极值点.(10分)
的极值点.(10分)
![]() 的变化如下:
的变化如下:
| x |
| x1 |
|
| ( |
|
| + | 0 | — | 0 | + |
由此,x=x1是函数F(x)的极大值点,x=x2是函数F(x)的极小值点.
综上所述,当且仅当![]()

(14分)