代数推理题怎么解
陕西永寿县中学 特级教师安振平
数学是“教会年轻人思考”的科学, 针对代数推理型问题, 我们不但要寻求它的解法是什么, 还要思考有没有其它的解法, 更要反思为什么要这样解, 不这样解行吗?我们通过典型的问题, 解析代数推理题的解题思路, 方法和技巧. 在解题思维的过程中, 既重视通性通法的演练, 又注意特殊技巧的作用, 同时将函数与方程, 数形结合, 分类与讨论, 等价与化归等数学思想方法贯穿于整个的解题训练过程当中.
例1设函数![]() ,已知
,已知![]() ,时恒有
,时恒有![]() ,求a的取值范围.
,求a的取值范围.
讲解: 由![]()
![]() ,
,
从而只要求直线L不在半圆C下方时, 直线L 的y截距的最小值.
当直线与半圆相切时,易求得![]() 舍去).
舍去).
故![]() .
.
本例的求解在于![]() 关键在于构造新的函数, 进而通过解几模型进行推理解题, 当中, 渗透着数形结合的数学思想方法,
显示了解题思维转换的灵活性和流畅性.
关键在于构造新的函数, 进而通过解几模型进行推理解题, 当中, 渗透着数形结合的数学思想方法,
显示了解题思维转换的灵活性和流畅性.
还须指出的是: 数形结合未必一定要画出图形, 但图形早已在你的心中了, 这也许是解题能力的提升, 还请三思而后行.
例2 已知不等式![]() 对于大于1的正整数n恒成立,试确定a的取值范围.
对于大于1的正整数n恒成立,试确定a的取值范围.
讲解: 构造函数![]() ,易证(请思考:用什么方法证明呢?)
,易证(请思考:用什么方法证明呢?)![]() 为增函数.
为增函数.
∵n是大于1的 正整数,
![]()
![]() 对一切大于1的正整数恒成立,必须
对一切大于1的正整数恒成立,必须![]() ,
,
即![]()
这里的构造函数和例1属于同类型, 学习解题就应当在解题活动的过程中不断的逐类旁通, 举一反三, 总结一些解题的小结论. 针对恒成立的问题, 函数最值解法似乎是一种非常有效的同法, 请提炼你的小结论.
例3 已知函数![]() 在区间[-b,1-b]上的最大值为25,求b的值.
在区间[-b,1-b]上的最大值为25,求b的值.
讲解: 由已知二次函数配方, 得 ![]()
![]() 时,
时,![]() 的最大值为4b2+3=25.
的最大值为4b2+3=25.
![]()
![]() 上递增,
上递增,
![]()
![]() 上递增,
上递增,
![]()
![]() .
.
关于二次函数问题是历年高考的热门话题, 值得读者在复课时重点强化训练. 针对抛物线顶点横坐标![]() 在不在区间[-b,1-b], 自然引出解题形态的三种情况,
这显示了分类讨论的数学思想在解题当中的充分运用. 该分就分, 该合就合, 这种辨证的统一完全依具体的数学问题而定, 需要在解题时灵活把握.
在不在区间[-b,1-b], 自然引出解题形态的三种情况,
这显示了分类讨论的数学思想在解题当中的充分运用. 该分就分, 该合就合, 这种辨证的统一完全依具体的数学问题而定, 需要在解题时灵活把握.
例4已知![]()
![]() 的单调区间;
的单调区间;
(2)若![]()
讲解: (1) 对 已 知 函 数 进 行 降 次 分 项 变 形 , 得 ![]() ,
,
![]()
(2)首先证明任意![]()
事实上,![]()
而 ![]()
![]()
![]()
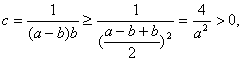
![]()
![]() .
.
函 数 与 不 等 式 证 明 的 综 合 题 在 高 考 中 常 考 常 新
, 是 既 考 知 识 又 考 能 力 的 好 题 型 , 在 高 考
备 考 中 有 较 高 的 训 练 价 值.. 针对本例的求解, 你能够想到证明任意![]() 采用逆向分析法, 给出你的想法!
采用逆向分析法, 给出你的想法!
例5 已知函数f(x)=![]() (a>0,a≠1).
(a>0,a≠1).
(1) 证明函数f(x)的图象关于点P(![]() )对称.
)对称.
(2) 令an=![]() ,对一切自然数n,先猜想使an>n2成立的最小自然数a,并证明之.
,对一切自然数n,先猜想使an>n2成立的最小自然数a,并证明之.
(3) 求证:![]() ∈N).
∈N).
讲解: (1)关于函数的图象关于定点P对称, 可采用解几中的坐标证法.
设M(x,y)是f(x)图象上任一点,则M关于P(![]() )的对称点为M’(1-x,1-y),
)的对称点为M’(1-x,1-y),
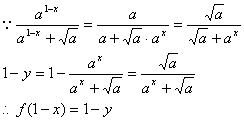
∴M′(1-x,1-y)亦在f(x)的图象上,
故函数f(x)的图象关于点P(![]() )对称.
)对称.
(2)将f(n)、f(1-n)的表达式代入an的表达式,化简可得an=an猜a=3,
即3n>n2.
下面用数学归纳法证明.
设n=k(k≥2)时,3k>k2.
那么n=k+1,3k+1>3·3k>3k2
又3k2-(k+1)2=2(k-![]() )2-
)2-![]() ≥0(k≥2,k∈N)
≥0(k≥2,k∈N)
∴3n>n2.
(3)∵3k>k2
∴klg3>2lgk
令k=1,2,…,n,得n个同向不等式,并相加得:
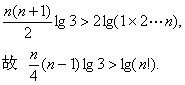
函数与数列综合型问题在高考中频频出现,是历年高考试题中的一道亮丽的风景线.针对本例,你能够猜想出最小自然数a=3吗? 试试你的数学猜想能力.
例6 已知二次函数![]() ,设方程
,设方程![]() 的两个实根为x1和x2.
的两个实根为x1和x2.
(1)如果![]() ,若函数
,若函数![]() 的对称轴为x=x0,求证:x0>-1;
的对称轴为x=x0,求证:x0>-1;
(2)如果![]() ,求b的取值范围.
,求b的取值范围.
讲解:(1)设![]() ,由
,由![]() 得
得![]() , 即
, 即
![]()
![]() ,
,
故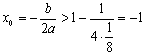 ;
;
(2)由![]()
![]() 同号.
同号.
①若![]() .
.
又![]() ,负根舍去)代入上式得
,负根舍去)代入上式得
![]() ,解得
,解得![]() ;
;
②若![]() 即4a-2b+3<0.
即4a-2b+3<0.
同理可求得![]() .
.
故当![]()
对你而言, 本例解题思维的障碍点在哪里, 找找看, 如何排除? 下一次遇到同类问题, 你会很顺利的克服吗? 我们力求做到学一题会一类, 不断提高逻辑推理能力.
例7 对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点。如果函数
的不动点。如果函数![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
讲解: 依题意有![]() ,化简为
,化简为 ![]() 由违达定理, 得
由违达定理, 得
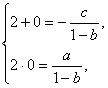
解得 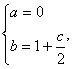 代入表达式
代入表达式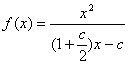 ,由
,由![]()
得 ![]() 不止有两个不动点,
不止有两个不动点,
![]()
(2)由题设得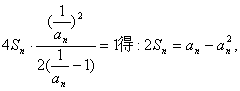 (*)
(*)
且![]() (**)
(**)
由(*)与(**)两式相减得:
![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ,由
,由![]() ,若
,若![]() 这与
这与![]() 矛盾,
矛盾,![]() ,即{
,即{![]() 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列,![]() ;
;
(3)采用反证法,假设![]() 则由(1)知
则由(1)知![]()
![]() ,有
,有
![]() ,而当
,而当![]() 这与假设矛盾,故假设不成立,
这与假设矛盾,故假设不成立,![]() .
.
关于本例的第(3)题,我们还可给出直接证法,事实上:
由![]() 得
得![]() <0或
<0或![]()
![]() 结论成立;
结论成立;
若![]()
![]() ,此时
,此时![]() 从而
从而![]() 即数列{
即数列{![]() }在
}在![]() 时单调递减,由
时单调递减,由![]() ,可知
,可知![]() 上成立.
上成立.
比较上述两种证法,你能找出其中的异同吗? 数学解题后需要进行必要的反思, 学会反思才能长进.
例8 设a,b为常数,![]() :把平面上任意一点
:把平面上任意一点
(a,b)映射为函数![]()
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当![]() ,这里t为常数;
,这里t为常数;
(3)对于属于M的一个固定值![]() ,得
,得![]() ,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象.
,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象.
讲解: (1)假设有两个不同的点(a,b),(c,d)对应同一函数,即![]() 与
与![]() 相同,
相同,
即 ![]() 对一切实数x均成立.
对一切实数x均成立.
特别令x=0,得a=c;令![]() ,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
故不存在两个不同点对应同函数.
(2)当![]() 时,可得常数a0,b0,使
时,可得常数a0,b0,使
![]()
=![]()
由于![]() 为常数,设
为常数,设![]() 是常数.
是常数.
从而![]() .
.
(3)设![]() ,由此得
,由此得![]()
![]() 在映射F之下,
在映射F之下,![]() 的原象是(m,n),则M1的原象是
的原象是(m,n),则M1的原象是
![]() .
.
消去t得![]() ,即在映射F之下,M1的原象
,即在映射F之下,M1的原象![]() 是以原点为圆心,
是以原点为圆心,![]() 为半径的圆.
为半径的圆.
本题将集合, 映射, 函数综合为一体, 其典型性和新颖性兼顾, 是一道用“活题考死知识”的好题目, 具有很强的训练价值.
例9 已知函数f(t)满足对任意实数x、y都有f(x+y)=f(x)+f(y)+xy+1,且f(-2)=-2.
(1)求f(1)的值;
(2)证明:对一切大于1的正整数t,恒有f(t)>t;
(3)试求满足f(t)=t的整数t的个数,并说明理由.
讲解 (1)为求f(1)的值,需令![]()
令![]() .
.
令![]() .
.
(2)令![]() (※)
(※)
![]() .
.
由![]() ,
,
![]() ,
,
于是对于一切大于1的正整数t,恒有f(t)>t.
(3)由※及(1)可知![]() .
.
下面证明当整数![]() .
.
![]() (※)得
(※)得![]()
即![]() ……,
……,
![]()
将诸不等式相加得
![]() .
.
综上,满足条件的整数只有t=1,![]() .
.
本题的求解显示了对函数方程f(x+y)=f(x)+f(y)+xy+1中的x、y取特殊值的技巧,这种赋值法在2002年全国高考第(21)题中得到了很好的考查.
例10 已知函数f(x)在(-1,1)上有定义,![]() 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有
![]() .
.
(1)证明:f(x)在(-1,1)上为奇函数;
(2)对数列![]() 求
求![]() ;
;
(3)求证![]()
讲解 (1)令![]() 则
则![]()
令![]() 则
则![]() 为奇函数.
为奇函数.
(2)![]() ,
, ![]()
![]() 是以-1为首项,2为公比的等比数列.
是以-1为首项,2为公比的等比数列.
![]()
(3)![]()
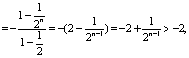
而 ![]()
![]()
本例将函数、方程、数列、不等式等代数知识集于一题,是考查分析问题和解决问题能力的范例. 在求解当中,化归出等比(等差)数列是数列问题常用的解题方法.