立体几何题怎么解
安振平
高考立体几何试题一般共有4道(客观题3道, 主观题1道), 共计总分27分左右,考查的知识点在20个以内. 选择填空题考核立几中的计算型问题, 而解答题着重考查立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着”多一点思考,少一点计算”的发展.从历年的考题变化看, 以多面体和旋转体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题.
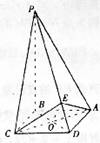
例1 四棱锥P—ABCD的底面是边长为a的正方形，PB⊥面ABCD.
（1）若面PAD与面ABCD所成的二面角为60°，求这个四棱锥的体积；
（2）证明无论四棱锥的高怎样变化，面PAD与面PCD所成的二面角恒大于90°
|
为
从而只要算出四棱锥的高就行了.
面ABCD,
∴BA是PA在面ABCD上的射影.又DA⊥AB，
∴PA⊥DA，
∴∠PAB是面PAD与面ABCD所成的二面角的平面角，
∠PAB=60°.
而PB是四棱锥P—ABCD的高，PB=AB·tg60°=
a,
.
（2）不论棱锥的高怎样变化，棱锥侧面PAD与PCD恒为全等三角形.
作AE⊥DP，垂足为E，连结EC，则△ADE≌△CDE，
是面PAD与面PCD所成的二面角的平面角.
设AC与DB相交于点O，连结EO，则EO⊥AC，
在
故平面PAD与平面PCD所成的二面角恒大于90°.
本小题主要考查线面关系和二面角的概念，以及空间想象能力和逻辑推理能力, 具有一定的探索性, 是一道设计新颖, 特征鲜明的好题.
|
，D为AB的中点.
（1）求证：AB1⊥平面CED；
（2）求异面直线AB1与CD之间的距离；
（3）求二面角B1—AC—B的平面角.
讲解:（1）∵D是AB中点，△ABC为等腰直角三角形，∠ABC=900，∴CD⊥AB又AA1⊥平面ABC，∴CD⊥AA1.
∴CD⊥平面A1B1BA ∴CD⊥AB1，又CE⊥AB1， ∴AB1⊥平面CDE；
（2）由CD⊥平面A1B1BA ∴CD⊥DE
∵AB1⊥平面CDE ∴DE⊥AB1
∴DE是异面直线AB1与CD的公垂线段
∵CE=，AC=1 , ∴CD=
∴
；
（3）连结B1C，易证B1C⊥AC，又BC⊥AC ,
∴∠B1CB是二面角B1—AC—B的平面角.
在Rt△CEA中，CE=，BC=AC=1,
∴∠B1AC=600
∴
， ∴
,
∴
, ∴
.
作出公垂线段和二面角的平面角是正确解题的前提, 当然, 准确地作出应当有严格的逻辑推理作为基石.
例3
如图a—l—
是120°的二面角，A，B两点在棱上，AB=2，D在
内，三角形ABD是等腰直角三角形，∠DAB=90°，C在内，
ABC是等腰直角三角形∠ACB=
（I）求三棱锥D—ABC的体积；
（2）求二面角D—AC—B的大小；
（3）求异面直线AB、CD所成的角.
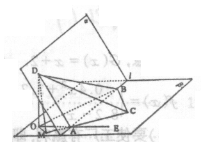
讲解: (1) 过D向平面做垂线，垂足为O，连强OA并延长至E.
为二面角a—l—的平面角.
.
是等腰直角三角形，斜边AB=2.
又D到平面的距离DO=
（2）过O在内作OM⊥AC,交AC的反向延长线于M,连结DM.则AC⊥DM.∴∠DMO 为二面角D—AC—B的平面角. 又在△DOA中，OA=2cos60°=1.且
（3）在平在内，过C作AB的平行线交AE于F，∠DCF为异面直线AB、CD所成的角. 
为等腰直角三角形，又AF等于C到AB的距离，即△ABC斜边上的高,
异面直线AB,CD所成的角为arctg
比较例2与例3解法的异同, 你会得出怎样的启示? 想想看.
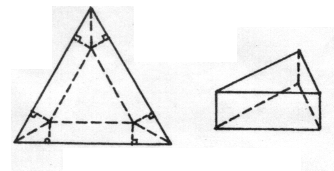
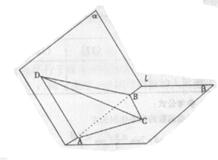
例4
|
图① 图②
讲解: 设容器的高为x．则容器底面正三角形的边长为
,
.
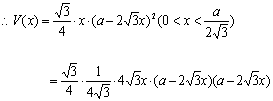
当且仅当 
.
故当容器的高为
时，容器的容积最大，其最大容积为
对学过导数的同学来讲，三次函数的最值问题用导数求解是最方便的，请读者不妨一试. 另外，本题的深化似乎与2002年全国高考文科数学压轴题有关，还请做做对照. 类似的问题是:
某企业设计一个容积为V的密闭容器，下部是圆柱形，上部是半球形，当圆柱的底面半径r和圆柱的高h为何值时，制造这个密闭容器的用料最省（即容器的表面积最小）.
例5 已知三棱锥P—ABC中，PC⊥底面ABC，AB=BC，
D、F分别为AC、PC的中点，DE⊥AP于E．
（1）求证：AP⊥平面BDE；
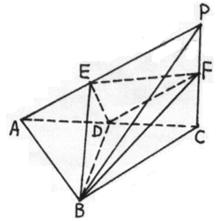
（2）求证：平面BDE⊥平面BDF；
（3）若AE∶EP=1∶2，求截面BEF分三棱锥
P—ABC所成两部分的体积比．
讲解: (1）∵PC⊥底面ABC，BD
平面ABC，∴PC⊥BD．
由AB=BC，D为AC的中点，得BD⊥AC．又PC∩AC=C，∴BD⊥平面PAC．
又PA平面、PAC，∴BD⊥PA．由已知DE⊥PA，DE∩BD=D，∴AP⊥平面BDE．
（2）由BD⊥平面PAC，DE平面PAC，得BD⊥DE．由D、F分别为AC、PC的中点，得DF//AP．
由已知，DE⊥AP，∴DE⊥DF. BD∩DF=D，∴DE⊥平面BDF．
又
DE平面BDE，∴平面BDE⊥平面BDF．
（3）设点E和点A到平面PBC的距离分别为h1和h2．则
h1∶h2=EP∶AP=2∶3,
故截面BEF分三棱锥P—ABC所成两部分体积的比为1∶2或2∶1
值得注意的是, “截面BEF分三棱锥P—ABC所成两部分的体积比”并没有说明先后顺序, 因而最终的比值答案一般应为两个, 希不要犯这种”会而不全”的错误.
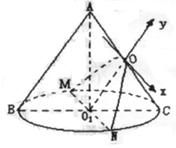
例6 已知圆锥的侧面展开图是一个半圆，它被过底面中心O1且平行于母线AB的平面所截，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）
为p的抛物线.
|
（1）求圆锥的母线与底面所成的角；
（2）求圆锥的全面积．
讲解: （1）设圆锥的底面半径为R，母线长为l，
由题意得：
,
即
,
所以母线和底面所成的角为
（2）设截面与圆锥侧面的交线为MON，其中O为截面与
AC的交点，则OO1//AB且
在截面MON内，以OO1所在有向直线为y轴，O为原点，建立坐标系，则O为抛物的顶点，所以抛物线方程为x2=－2py，点N的坐标为（R，－R），代入方程得
R2=－2p（－R），得R=2p，l=2R=4p.
∴圆锥的全面积为
.
将立体几何与解析几何相链接, 颇具新意, 预示了高考命题的新动向. 类似请思考如下问题:
一圆柱被一平面所截，截口是一个椭圆．已知椭圆的
长轴长为5，短轴长为4，被截后几何体的最短侧面母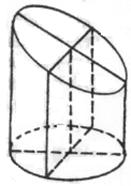 
线长为1，则该几何体的体积等于 ．
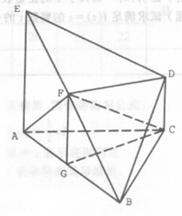
例7 如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a， DC=a，F、G分别为EB和AB的中点.
|
（2）求证：AF⊥BD；
(3) 求二面角B—FC—G的正切值.
讲解: ∵F、G分别为EB、AB的中点，
∴FG=
EA，又EA、DC都垂直于面ABC, FG=DC，
∴四边形FGCD为平行四边形，∴FD∥GC，又GC面ABC，
∴FD∥面ABC.
（2）∵AB=EA，且F为EB中点，∴AF⊥EB ① 又FG∥EA，EA⊥面ABC
∴FG⊥面ABC ∵G为等边△ABC，AB边的中点，∴AG⊥GC.
∴AF⊥GC又FD∥GC，∴AF⊥FD ②
由①、②知AF⊥面EBD，又BD面EBD，∴AF⊥BD.
（3）由（1）、（2）知FG⊥GB，GC⊥GB，∴GB⊥面GCF.
过G作GH⊥FC，垂足为H，连HB，∴HB⊥FC.
∴∠GHB为二面角B-FC-G的平面角.
易求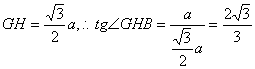
.
例8 如图，正方体ABCD—A1B1C1D1的棱长为1，P、Q分别是线段AD1和BD上的点，且
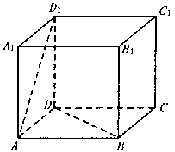D1P∶PA=DQ∶QB=5∶12.
(1) 求证PQ∥平面CDD1C1；
(2) 求证PQ⊥AD；
(3) 求线段PQ的长.
讲解: （1）在平面AD1内，作PP1∥AD与DD1交于点P1，在平面AC内，作
1∥BC交CD于点Q1，连结P1Q1.
∵ 
,
∴PP1
1 .
由四边形P1P1为平行四边形, 知PQ∥P1Q1
而P1Q1
平面CDD1C1， 所以PQ∥平面CDD1C1
（2）AD⊥平面D1DCC1， ∴AD⊥P1Q1，
又∵PQ∥P1Q1， ∴AD⊥PQ.
（3）由（1）知P1Q1 PQ,
，而棱长CD=1. ∴DQ1=
. 同理可求得 P1D=
.
在Rt△P1DQ1中，应用勾股定理, 立得
P1Q1=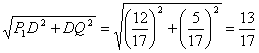
.
做为本题的深化, 笔者提出这样的问题: P, Q分别是BD,
上的动点,试求
的最小值, 你能够应用函数方法计算吗? 试试看. 并与如下2002年全国高考试题做以对照, 你会得到什么启示?
如图，正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动，点N在BF上移动，若CM=BN=
（1） 求MN的长；
（2） 当为何值时，MN的长最小；
（3）
当MN长最小时，求面MNA与面MNB所成的二面角的大小。
立体几何知识是复课耗时较多, 而考试得分偏底的题型. 只有放底起点, 依据课本, 熟化知识, 构建空间思维网络, 掌握解三角形的基本工具, 严密规范表述, 定会突破解答立几考题的道道难关.