数学开放性问题怎么解
陕西永寿县中学 特级教师安振平
数学开放性问题是近年来高考命题的一个新方向,其解法灵活且具有一定的探索性,这类题型按解题目标的操作模式分为:规律探索型,问题探究型,数学建模型,操作设计型,情景研究型.如果未知的是解题假设,那么就称为条件开放题;如果未知的是解题目标,那么就称为结论开放题;如果未知的是解题推理,那么就称为策略开放题.当然,作为数学高考题中的开放题其“开放度”是较弱的,如何解答这类问题,还是通过若干范例加以讲解.
例 1 设等比数列![]() 的公比为
的公比为 ![]() ,前
,前 ![]() 项和为
项和为 ![]() ,是否存在常数
,是否存在常数 ![]() ,使数列
,使数列 ![]() 也成等比数列?若存在,求出常数
也成等比数列?若存在,求出常数![]() ;若不存在,请 明 理 由.
;若不存在,请 明 理 由.
讲解 存在型开放题的求解一般是从假设存在入手, 逐步深化解题进程的.
设存在常数![]() , 使数列
, 使数列![]() 成等比数列.
成等比数列.
![]()
![]()
(i) 当 ![]() 时,
时,![]() 代入上式得
代入上式得
![]() 即
即![]() =0
=0
但![]() , 于是不存在常数
, 于是不存在常数![]() ,使
,使![]() 成等比数列.
成等比数列.
(ii) 当 ![]() 时,
时,![]() , 代 入 上 式 得
, 代 入 上 式 得
![]() .
.
综 上 可 知 , 存 在 常 数 ![]() ,使
,使![]() 成等比数列.
成等比数列.
等比数列n项求和公式中公比的分类, 极易忘记公比![]() 的 情 形, 可 不 要 忽 视 啊 !
的 情 形, 可 不 要 忽 视 啊 !
例2 某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3 ) 使用若干年后,对机床的处理方案有两种:
(i )当年平均盈利额达到最大值时,以30万元价格处理该机床;
(ii )当盈利额达到最大值时,以12万元价格处理该机床,问用哪种方案处理较为合算?请说明你的理由.
讲解 本例兼顾应用性和开放性, 是实际工作中经常遇到的问题.
(1)![]()
=![]() .
.
(2)解不等式 ![]() >0,
>0,
得 ![]() <x<
<x<![]() .
.
∵ x∈N, ∴ 3 ≤x≤ 17.
故从第3年工厂开始盈利.
(3)(i) ∵ ![]() ≤40
≤40![]()
当且仅当![]() 时,即x=7时,等号成立.
时,即x=7时,等号成立.
∴ 到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
(ii) ![]() y=-2x2+40x-98= -2(x-10)2 +102,
y=-2x2+40x-98= -2(x-10)2 +102,
![]() 当x=10时,ymax=102.
当x=10时,ymax=102.
故到2011年,盈利额达到最大值,工厂共获利102+12=114万元.
解答函数型最优化实际应用题,二、三元均值不等式是常用的工具.
例3 已知函数f(x)=![]() (x<-2)
(x<-2)
(1)求f(x)的反函数f-1(x);
(2)设a1=1,![]() =-f-1(an)(n∈N),求an;
=-f-1(an)(n∈N),求an;
(3)设Sn=a12+a22+…+an2,bn=Sn+1-Sn是否存在最小正整数m,使得对任意n∈N,有bn<![]() 成立?若存在,求出m的值;若不存在说明理由.
成立?若存在,求出m的值;若不存在说明理由.
讲解 本例是函数与数列综合的存在性问题, 具有一定的典型性和探索性.
(1) y=![]() ,
,
∵x<-2,∴x= -![]() ,
,
即y=f-1(x)=
- ![]() (x>0).
(x>0).
(2) ∵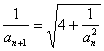 , ∴
, ∴![]() =4.
=4.
∴{![]() }是公差为4的等差数列.
}是公差为4的等差数列.
∵a1=1, ∴![]() =
=![]() +4(n-1)=4n-3.
+4(n-1)=4n-3.
∵an>0 , ∴an=![]() .
.
(3) bn=Sn+1-Sn=an+12=![]() , 由bn<
, 由bn<![]() ,得 m>
,得 m>![]() 对于n∈N成立.
对于n∈N成立.
∵![]() ≤5 ,
≤5 ,
∴m>5,存在最小正数m=6,使得对任意n∈N有bn<![]() 成立.
成立.
为了求an ,我们先求![]() ,这是因为{
,这是因为{![]() }是等差数列, 试问: 你能够想到吗? 该题是构造等差数列的一个典范.
}是等差数列, 试问: 你能够想到吗? 该题是构造等差数列的一个典范.
例4 已知数列![]() 在直线x-y+1=0上.
在直线x-y+1=0上.
(1) 求数列{an}的通项公式;
(2)若函数![]()
求函数f(n)的最小值;
(3)设![]() 表示数列{bn}的前n项和.试问:是否存在关于n 的整式g(n), 使得
表示数列{bn}的前n项和.试问:是否存在关于n 的整式g(n), 使得![]() 对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,说明理由.
对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,说明理由.
讲解 从 规 律 中 发 现 ,从 发 现 中 探 索.
(1)![]()
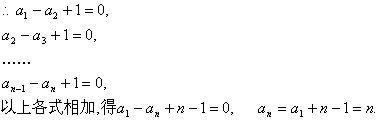
(2) ![]()
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
(3)![]() ,
,
![]()
![]() .
.
![]()
![]()
![]()
故存在关于n的整式![]() 使等式对于一切不小2的自然数n恒成立.
使等式对于一切不小2的自然数n恒成立.
事实上, 数列{an}是等差数列, 你知道吗?
例5 深夜,一辆出租车被牵涉进一起交通事故,该市有两家出租车公司——红色出租车公司和蓝色出租车公司,其中蓝色出租车公司和红色出租车公司分别占整个城市出租车的85%和15%。据现场目击证人说,事故现场的出租车是红色,并对证人的辨别能力作了测试,测得他辨认的正确率为80%,于是警察就认定红色出租车具有较大的肇事嫌疑. 请问警察的认定对红色出租车公平吗?试说明理由.
讲解 设该城市有出租车1000辆,那么依题意可得如下信息:
| 证人所说的颜色(正确率80%) | ||||
| 真 实 颜 色 | 蓝色 | 红色 | 合计 | |
| 蓝色(85%) | 680 | 170 | 850 | |
| 红色(15%) | 30 | 120 | 150 | |
| 合计 | 710 | 290 | 1000 | |
从表中可以看出,当证人说出租车是红色时,且它确实是红色的概率为![]() ,而它是蓝色的概率为
,而它是蓝色的概率为![]() . 在这种情况下,以证人的证词作为推断的依据对红色出租车显然是不公平的.
. 在这种情况下,以证人的证词作为推断的依据对红色出租车显然是不公平的.
本题的情景清新, 涉及到新教材中概率的知识, 上述解法中的列表技术显示了一定的独特性, 在数学的应试复课中似乎是很少见的.
例6 向明中学的甲、乙两同学利用暑假到某县进行社会实践,对该县的养鸡场连续六年来的规模进行调查研究,得到如下两个不同的信息图:
|
(A)图表明:从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡;
(B)图表明:由第1年养鸡场个数30个减少到第6年的10个.
请你根据提供的信息解答下列问题:
(1)第二年的养鸡场的个数及全县出产鸡的总只数各是多少?
(2)哪一年的规模最大?为什么?
![]() 讲解 (1)设第n年的养鸡场的个数为
讲解 (1)设第n年的养鸡场的个数为![]() ,平均每个养鸡场出产鸡
,平均每个养鸡场出产鸡![]() 万只,
万只,
由图(B)可知, ![]() =30,
=30,![]() 且点
且点![]() 在一直线上,
在一直线上,![]()
从而
![]()
由图(A)可知, ![]() 且点
且点![]() 在一直线上,
在一直线上,![]()
于是 ![]()
![]() =
=![]() (万只),
(万只),![]() (万只)
(万只)
第二年的养鸡场的个数是26个,全县出产鸡的总只数是31.2万只;
(2)由![]() (万只),
(万只),
第二年的养鸡规模最大,共养鸡31.2万只.
有时候我们需要画出图形, 有时候我们却需要从图形中采集必要的信息, 这正反映了一个事物的两个方面. 看来, 读图与识图的能力是需要不断提升的.
例7 已知动圆过定点P(1,0),且与定直线![]() 相切,点C在l上.
相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-![]() 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
讲解 本例主要考查直线、圆与抛物线的基本概念及位置关系,是解析几何中的存在性问题.
(1)由曲线M是以点P为焦点,直线l为准线的抛物线,知曲线M的方程为![]() .
.
(2)(i)由题意得,直线AB的方程为![]() 消y得
消y得
![]()
于是, A点和B点的坐标分别为A![]() ,B(3,
,B(3,![]() ),
),![]()
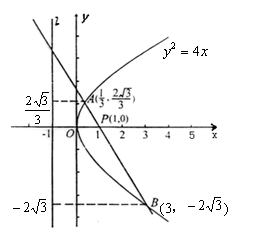 假设存在点C(-1,y),使△ABC为正三角形,则BC=AB且AC=AB,
假设存在点C(-1,y),使△ABC为正三角形,则BC=AB且AC=AB,
即有
|
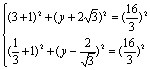
由①-②得![]()
![]()
因为![]() 不符合①,所以由①,②组成的方程组无解.
不符合①,所以由①,②组成的方程组无解.
故知直线l上不存在点C,使得△ABC是正三角形.
(ii)设C(-1,y)使△ABC成钝角三角形,
由![]()
即当点C的坐标是(-1,![]() )时,三点A,B,C共线,故
)时,三点A,B,C共线,故![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
(i) 当![]() ,即
,即![]() ,
,
即![]() 为钝角.
为钝角.
(ii) 当![]() ,即
,即![]() ,
,
即![]() 为钝角.
为钝角.
(iii)当![]() ,即
,即![]() ,
,
即![]() . 该不等式无解,所以∠ACB不可能为钝角.
. 该不等式无解,所以∠ACB不可能为钝角.
故当△ABC为钝角三角形时,点C的纵坐标y的取值范围是![]() .
.
需要提及的是, 当△ABC为钝角三角形时, 钝角的位置可能有三个,需要我们进行一一探讨.
例8 已知![]() 是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足关系式
是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足关系式 ![]() .
.
(1)求f(0),f(1)的值;
(2)判断![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(3)若![]() ,求数列{un}的前n项的和Sn.
,求数列{un}的前n项的和Sn.
讲解 本题主要考查函数和数列的基本知识,考查从一般到特殊的取特值求解技巧.
(1)在![]() 中,令
中,令![]() 得
得
![]() .
.
在![]() 中,令
中,令![]() 得
得
![]() ,有
,有 ![]() .
.
(2)![]() 是奇函数,这需要我们进一步探索. 事实上
是奇函数,这需要我们进一步探索. 事实上
![]()
![]()
![]()
![]()
故![]() 为奇函数.
为奇函数.
(2) 从规律中进行探究,进而提出猜想.
由 ![]()
![]() ,
,
………………………………
猜测 ![]() .
.
于是我们很易想到用数学归纳法证明.
1° 当n=1时,![]() ,公式成立;
,公式成立;
2°假设当n=k时,![]() 成立,那么当n=k+1时,
成立,那么当n=k+1时,
![]() ,公式仍然成立.
,公式仍然成立.
综上可知,对任意![]() 成立.
成立.
从而 ![]() .
.
![]()
![]()
![]()
![]() ,
,![]() .
.
故 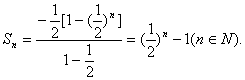
例9 若![]() 、
、![]() ,
,![]()
![]()
(1)求证:![]() ;
;
(2)令![]() ,写出
,写出![]() 、
、![]() 、
、![]() 、
、![]() 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式![]() ;
;
(3)证明:存在不等于零的常数p,使![]() 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.
讲解 (1)采用反证法. 若![]() ,即
,即![]() , 解得
, 解得 ![]()
从而![]() 与题设
与题设![]() ,
,![]() 相矛盾,
相矛盾,
故![]() 成立.
成立.
(2) ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() .
.
(3)因为![]() 又
又![]() ,
,
所以![]() ,
,
因为上式是关于变量![]() 的恒等式,故可解得
的恒等式,故可解得![]() 、
、![]() .
.
我们证明相等的问题太多了,似乎很少见到证明不相等的问题,是这样吗?
例10 如图,已知圆A、圆B的方程分别是![]() 动圆P与圆A、圆B均外切,直线l的方程为:
动圆P与圆A、圆B均外切,直线l的方程为:![]() .
.
(1)求圆P的轨迹方程,并证明:当![]() 时,点P到点B的距离与到定直线l距离的比为定值;
时,点P到点B的距离与到定直线l距离的比为定值;![]()
(2) 延长PB与点P的轨迹交于另一点Q,求![]() 的最小值;
的最小值;
(3)如果存在某一位置,使得PQ的中点R在l上的射影C,满足![]() 求a的取值范围.
求a的取值范围.

讲解(1)设动圆P的半径为r,则|PA|=r+![]() ,|PB = r +
,|PB = r + ![]() ,
,
∴ PA -|PB = 2.
∴ 点P的轨迹是以A、B为焦点,焦距为4,实轴长为2的双曲线的右准线的右支,其方程为 ![]() (x ≥1).若
(x ≥1).若![]() , 则l的方程
, 则l的方程![]() 为双曲线的右准线, ∴点P到点B的距离与到l的距离之比为双曲线的离心率e
= 2.
为双曲线的右准线, ∴点P到点B的距离与到l的距离之比为双曲线的离心率e
= 2.
(2)若直线PQ的斜率存在,设斜率为k,则直线PQ的方程为y = k ( x-2 )代入双曲线方程, 得
![]()
![]()
由 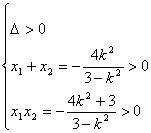 , 解得
, 解得![]() >3.
>3.
∴ |PQ|=![]() .
.
当直线的斜率存在时,![]() ,得
,得![]() ,|PQ=6.
,|PQ=6.
∴ |PQ的最小值为6.
(3)当PQ⊥QC时,P、C、Q构成Rt△.
∴ R到直线l的距离|RC=![]() ①
①
又 ∵ 点P、Q都在双曲线![]() 上,
上,
∴ 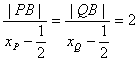 .
.
∴ ![]() ,即
,即 ![]() .
.
∴ ![]() ②
②
将②代入①得 ![]() ,|PQ|=2-4a≥6.
,|PQ|=2-4a≥6.
故有a≤-1.
“如果存在”并不意味着一定存在, 如何修改本题使其成为不存在的范例呢? 问题的提出既能延伸我们的思绪, 更能完善我们的知识技能, 无形中使解题能力得到逐渐的提升.