东华高级中学高三(上)期中考试试卷(数学)
命题人:刘则礼 审题人:朱效东 5005.10.28
温馨提示:请使用黑色碳素笔答题,解答要规范,书写要整洁,心态要端正,审题要清楚,运算要准确;高三全体数学老师祝福你――考出自已满意的成绩。
一、 选择题:本大题共 10 小题;每小题 5 分,满分 50 分。在每小题给出的四个选项中,只有一项是符合题目要求的。请将答案填入答题卡中。
1. 已知集合A
=![]() ,且B
,且B![]() A,则集合B的个数为 ( )
A,则集合B的个数为 ( )
A.3个 B.4个 C.8个 D.16个
2.设数列![]() 是等差数列,且
是等差数列,且![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,则( )
项和,则( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.若![]() 的终边所在象限是
( )
的终边所在象限是
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知f (x)=x5+ax3+bx-8,且f (-2)=10,那么f (2)等于( )。
A 10 B -10 C -18 D -26
5.函数![]() 的反函数是 ( )
的反函数是 ( )
A.y=x2-2x+2(x<1) B.y=x2-2x+2(x≥1)
C.y=x2-2x (x<1) D.y=x2-2x (x≥1)
6.一元二次方程![]() 有一个正根和一个负根的充分不必要条件是: A.
有一个正根和一个负根的充分不必要条件是: A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() 是第三象限角,
是第三象限角,![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若函数y=log![]() (2-log2x)的值域是(0,
+∞),则其定义域是( )。
(2-log2x)的值域是(0,
+∞),则其定义域是( )。
A (-∞, 2) B (0, 2) C (0, 4) D (2, 4)
9.定义在R上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为( )A.
的值为( )A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.把数列{2n+1}依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)…则第104个括号内各数之和为( ) A. 2036 B。2048 C。 2060 D。2072
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
11. 在等差数列{an}中,若a4+a6+a8+a10+a12=120,则2a10-a12= .
12.如果f(a+b)=f(a)•f(b)且f(1)=2,则![]() +
+![]() +
+![]() +…+
+…+![]() .
.
13.已知![]() 为锐角,
为锐角,![]() ,
,![]() ,则
,则![]() =
.
=
.
14.用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块,…,依次类推,每一层都用去了上层剩下的砖块的一半多一块,如果到第九层恰好砖块用完,那么一共用了 块砖.
三、解答题(本大题共80分.解答应写出文字说明、证明过程或演算步骤)
15.(12分) 已知函数![]()
(1)求![]() 的最小正周期;(2)求
的最小正周期;(2)求![]() 的单调递减区间;
的单调递减区间;
(3)函数![]() 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
16.(12分)我校高三举行三人投篮比赛,比赛规定:每投中一个球得100分,没投中得
-100分.假设某班三同学每人投中的概率均为0.8,且每人投中与否相互之间没有影响.
(Ⅰ)求这三位同学每人各投一次总得分![]() 的概率分布和数学期望;
的概率分布和数学期望;
(Ⅱ)求这三位同学总得分不为负分的概率.
17.(14分)已知数列![]() 其前n项和为Sn,且S1=2,当
其前n项和为Sn,且S1=2,当![]() 时,Sn=2an. (1)求数列
时,Sn=2an. (1)求数列![]() 的通项公式; (2)若
的通项公式; (2)若![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
18.(14分)某地区预计明年从年初开始的前x个月内,对某种商品的需求总量![]() (万件)与月份x的近似关系为:
(万件)与月份x的近似关系为:![]() ,且
,且![]() .
.
(1)写出明年第x个月的需求量![]() (万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(2)如果将该商品每月都投放市场p万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问:p至少为多少万件?
19.(14分)设![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,且
,且![]()
![]() ,当
,当![]() 时,
时,![]() ,求:
,求:
(1) ![]() 及
及![]() 的值; (2)函数
的值; (2)函数![]() 的单调递增区间;
的单调递增区间;
(3) ![]() 时,
时,![]() ,求
,求![]() ,并猜测
,并猜测![]()
![]() 时,
时,![]() 的表达式.
的表达式.
20.(14分) 已知函数![]() ,
,![]() (
(![]() 为正常数),且函数
为正常数),且函数![]() 与
与![]() 的图象在
的图象在![]() 轴上的截距相等。(1)求
轴上的截距相等。(1)求![]() 的值;(2)求函数
的值;(2)求函数![]() 的单调递增区间;(3)若
的单调递增区间;(3)若![]() 为正整数,证明:
为正整数,证明:![]() .
.
东华高级中学高三(上)期中考试(数学)答案卷
二. 填空题(每题5分,合计20分)
13 . 14 . 15 . 16 .
三、解答题:
15(12分):
16(12分):
17(14分)
18(14分):
19(14分):
20(14分):
东华高级中学高三(上)期中考试(数学)答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 答案 | C | B | D | D | B | C | B | D | D | D |
二、填空题
11
24.
12 2006. 13. ![]() 14 1022.
14 1022.
三.解答题:
15. (Ⅰ)由![]()
由![]() ……2分
……2分
![]() ……6分
……6分
∴函数![]() 的最小正周期T=
的最小正周期T=![]() ……7分
……7分
(Ⅱ)由![]()
∴![]() 的单调递减区间是
的单调递减区间是![]()
![]() .
……10分
.
……10分
(Ⅲ)![]() ,
,
∴奇函数![]() 的图象左移
的图象左移![]() 即得到
即得到![]() 的图象,
的图象,
故函数![]() 的图象右移
的图象右移![]() 个单位后对应的函数成为奇函数. ……12分
个单位后对应的函数成为奇函数. ……12分
(注:第Ⅲ问答案不唯一)
16.(1)
|
| -300 | -100 | 100 | 300 |
| p | 0.008 | 0.096 | 0.384 | 0.512 |
E![]() =180. (2)0.896
=180. (2)0.896
17.(1)当n=1时,![]() ;
;
当n=2时,有![]() ;
;
当![]() 时,有
时,有![]() .
.
故该数列从第2项起为公比q=2的等比数列,故
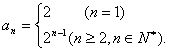
(2)由(1)知 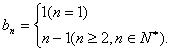
故数列![]() 的前n项和
的前n项和 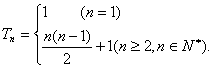
即:![]()
18.(1)![]() .当x≥2时,
.当x≥2时,
![]()
![]()
![]()
![]()
![]() .
.
∴ ![]() ,且
,且![]() .
.
∵ ![]() .
.
∴ 当x=12-x,即x=6时,![]() (万件).故6月份该商品的需求量最大,最大需求量为
(万件).故6月份该商品的需求量最大,最大需求量为![]() 万件.
万件.
(2)依题意,对一切![]() {1,2,…,12}有
{1,2,…,12}有![]() .
.
∴ ![]() (x=1,2,…,12).
(x=1,2,…,12).
∵ ![]()
![]()
∴ ![]() . 故 p≥1.14.故每个月至少投放1.14万件,可以保证每个月都保证供应.
. 故 p≥1.14.故每个月至少投放1.14万件,可以保证每个月都保证供应.
19.(1)![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
(2)![]() ,
,![]() 的增区间为
的增区间为![]() .
.
(3)![]()
![]() ,
,![]() ,所以
,所以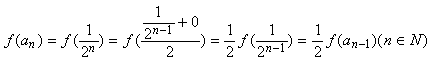 ,
,
因此![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,故
的等比数列,故![]() ,猜测
,猜测![]() .
.
20.(1)由题意,![]() ,
,![]() 又
又![]() ,所以
,所以![]() 。
。
(2)![]()
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增。
上单调递增。
(3)设![]() ,考查数列
,考查数列![]() 的变化规律:
的变化规律:
解不等式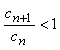 ,由
,由![]() ,上式化为
,上式化为![]()
解得![]() ,因
,因![]() 得
得![]() ,于是
,于是![]() ,而
,而![]()
所以![]() 。
。
