高邮市界首中学2005—2006学年高三第三次质量检测
数 学 试 卷 2005.10.20
命题人:蒋寅
第I卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.“![]() ”是“
”是“![]() 且
且![]() ”的 ( )
”的 ( )
(A) 充分非必要条件 (B)必要非充分条件 (C)充要条件 (D)既不充分也不必要条件
2.在各项都为正数的等比数列![]() 中,首项
中,首项![]() ,前三项和为21,则
,前三项和为21,则![]() ( )
( )
(![]() )33 (
)33 (![]() )72 (
)72 (![]() )84 (
)84 (![]() )189
)189
3.若点P在![]() 的终边上,且OP=2,则点P的坐标
( )
的终边上,且OP=2,则点P的坐标
( )
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
4.设向量a=(-1,2),b=(2,-1),则(a·b)(a+b)等于 ( )
A.(1,1) B.(-4,-4) C. -4 D.(-2,-2)
5.若某等差数列{an}中,![]() 为一个确定的常数,则其前n项和
为一个确定的常数,则其前n项和![]() 中也为确定的常数的A.
中也为确定的常数的A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 其定义域
其定义域![]() 分成了四个单调区间,则实数
分成了四个单调区间,则实数![]() 满足( )
满足( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.某人为了观看2008奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年5月10日将所有存款和利息全部取回,则可取回的钱的总数(元)为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() 的周期与函数
的周期与函数![]() 的周期相等,则
的周期相等,则![]() 等于
等于
(A)2 (B)1 (C)![]() (D)
(D)![]()
9.函数![]() 的大致图象是
( )
的大致图象是
( )
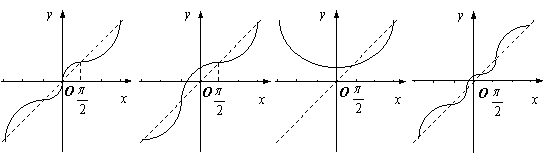
A. B. C. D.
10.已知函数![]() 对于任意x,y∈R,都有
对于任意x,y∈R,都有![]() ,且f(1)=2
,且f(1)=2
![]() 不能等于
( )
不能等于
( )
A.![]() B.
B.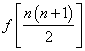 C.
C.![]() D.
D.![]()
11.若![]() 是定义在R上的奇函数且
是定义在R上的奇函数且![]() ,给出下列4个结论:其中不正确的结论是
,给出下列4个结论:其中不正确的结论是
A.![]() B.
B. ![]() 是以4为周期的函数
是以4为周期的函数
C.![]() 的图像关于直线
的图像关于直线![]() 对称 D.
对称 D. ![]()
12. 有限数列A=(a1,a2,…,an),![]() 为其前
为其前![]() 项和,定义为A的“凯森和”;如有2004项的数列(a1,a2,…,a2004)的“凯森和”为2005,则有2005项的数列(1,a1,a2,…,a2004)的“凯森和”为
( )
项和,定义为A的“凯森和”;如有2004项的数列(a1,a2,…,a2004)的“凯森和”为2005,则有2005项的数列(1,a1,a2,…,a2004)的“凯森和”为
( )
A.2004 B.2005 C.2006 D.2008
第Ⅱ卷(主观题,共90分)
二、填空题(本大题共6小题,每小题4分,共24分。)
13.![]() ___ __________
___ __________
14.若函数![]() 的图象关于直线
的图象关于直线![]() 对称,则实数
对称,则实数![]() =___________.
=___________.
15.已知向量![]() ,且A、B、C三点共线,则k= .
,且A、B、C三点共线,则k= .
16、设数列![]() 的前n项的和
的前n项的和![]() ,则
,则![]() 。
。
17. 在ΔABC中,O为中线AM上的一个动点,若AM=2,则![]() 的最小值为____。
的最小值为____。
18.对于函数![]() ,给出下列命题:①f (x)有最小值;②当a=0时,
,给出下列命题:①f (x)有最小值;②当a=0时,
f (x)的值域为R;③当a>0时,f (x)在区间![]() 上有反函数;④若f (x)在区间
上有反函数;④若f (x)在区间
![]() 上是增函数,则实数a的取值范围是
上是增函数,则实数a的取值范围是![]() . 上述命题中正确的是
. 上述命题中正确的是
(填上所有正确命题序号) .
三、解答题(本大题共5小题;共66分)解答应写出文字说明、演算步骤或证明过程。
19.(本小题满分12分,每小问满分6分)
已知等比数列![]() 中,
中,![]() .
.
(Ⅰ) 求通项![]() ;
;
(Ⅱ) 若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,求
,求![]() 的值
的值
20(本小题满分12分,每小问满分6分)
已知![]() ,
,![]() ,记
,记![]() .
.
(1) 求![]() 的周期及最小值;
的周期及最小值;
(2) 若![]() 按m平移得到
按m平移得到![]() , 求向量m .
, 求向量m .
21. (本小题满分12分)
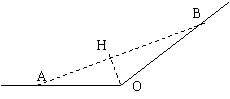 如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修一条铁路L,L在AO上设一站A,在OB上设一站B,铁路在AB部分视为直线段,现要求市中心O与AB的距离为10km,问把A、B分别设在距公路中心O多远的地方才能使
如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修一条铁路L,L在AO上设一站A,在OB上设一站B,铁路在AB部分视为直线段,现要求市中心O与AB的距离为10km,问把A、B分别设在距公路中心O多远的地方才能使![]() 最小,并求出最短距离。
最小,并求出最短距离。
22. (本小题满分14分)
对于定义域为D的函数![]() ,若同时满足下列条件:
,若同时满足下列条件:
①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() 上的值域为[a,b];那么把
上的值域为[a,b];那么把![]() 叫闭函数.
叫闭函数.
(I)求闭函数![]() 符合条件②的区间[a,b]
符合条件②的区间[a,b]
(II)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(III)若![]() 是闭函数,求实数k的范围.
是闭函数,求实数k的范围.
23.(本小题满分16分)
设![]() 为正整数,规定:
为正整数,规定:![]() ,已知
,已知![]()
![]() .
.
(1)解不等式:![]() ;
;
(2)设集合![]() ,对任意
,对任意![]() ,证明:
,证明:![]() ;
;
(3)求![]() 的值;
的值;
(4)若集合![]() ,证明:
,证明:![]() 中至少包含有
中至少包含有![]() 个元素.
个元素.
高邮市界首中学2005—2006学年高三
第二次质量检测答题纸
| 第Ⅱ卷 非选择题 (共90分) |
| 二.填空题: 13题 |
|
14题 |
| 15题 |
| 16题 |
| 17题 |
| 18题 |
| 三.解答题: 19题 解: |
| 20题 解:
|
| 21题 解:
|
| 22题 解:
|
|
解: |
|
|
高三第三次质量检测答案 05.10.19
一、选择题
B C D B B D A C B A C B
二、填空题
13. ![]() 14. -2 15.
14. -2 15. ![]() 16 153 17. –2 18.②③
16 153 17. –2 18.②③
三、解析题
19解:(Ⅰ) 设等比数列![]() 的公比为
的公比为![]() ,则
,则
![]() ……………………………………………………(2分)
……………………………………………………(2分)
解之得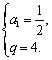 .……………………………………………………(4分)
.……………………………………………………(4分)
∴![]() .………………………………………(6分)
.………………………………………(6分)
(Ⅱ) ![]() .……………………………………(8分)
.……………………………………(8分)
∵![]() ,
,
∴![]() 是首项为
是首项为![]() ,公差为2的等差数列.
,公差为2的等差数列.
∴![]() .………………………………………(10分)
.………………………………………(10分)
∴![]() ,∴
,∴![]() 或
或![]() (舍去).
(舍去).
因此,所求![]() .……………………………………………………(12分)
.……………………………………………………(12分)
20. 解:(1)![]() …………(2分)
…………(2分)
=![]() …………(6分)
…………(6分)
∴![]() 的周期为π,最小值为-2. …………(8分)
的周期为π,最小值为-2. …………(8分)
(2)若![]() 按向量m平移得到
按向量m平移得到![]()
则向量m![]()
![]() …………(12分)
…………(12分)
21. 解:设AO=a,OB=b,
∵AO在正西方向,OB在东北方向 ∴∠AOB=135°…………(2分)
∴![]() (当且仅当a=b时等号成立) …………(4分)
(当且仅当a=b时等号成立) …………(4分)
又O到AB的距离为10,设∠AOB=α 则∠OBA=![]()
∴![]()
∴![]() …………(8分)
…………(8分)
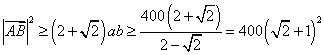 …………(10分)
…………(10分)
∴当且仅当a=b=10![]() 时,
时,![]() 最小,其最短距离为20
最小,其最短距离为20![]() …………(12分)
…………(12分)
22解:(1)由题意,![]() 上递减,则
上递减,则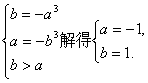
所以,所求的区间为[-1,1] …………(4分)
(2)当![]()
![]() .
.
所以,函数在定义域上不单调递增或单调递减,从而该函数不是闭函数. …………(8分)
(3)若![]() 是闭函数,则存在区间[a,b],在区间[a,b]上,函数
是闭函数,则存在区间[a,b],在区间[a,b]上,函数![]() 的值
的值
域为[a,b],即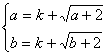
![]() 的两个实数根,
的两个实数根,
即方程![]() 有两个不等的实根. …………(10分)
有两个不等的实根. …………(10分)
当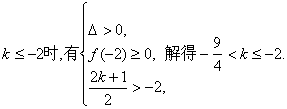
当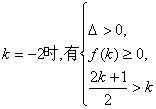 此不等式组无解.
此不等式组无解.
综上所述,![]() ………… (14分)
………… (14分)
23.解:(1)①当0≤![]() ≤1时,由
≤1时,由![]() ≤
≤![]() 得,
得,![]() ≥
≥![]() .∴
.∴![]() ≤
≤![]() ≤1.
≤1.
②当1<![]() ≤2时,因
≤2时,因![]() ≤
≤![]() 恒成立.∴1<
恒成立.∴1<![]() ≤2.
≤2.
由①,②得,![]() ≤
≤![]() 的解集为{
的解集为{![]()
![]() ≤
≤![]() ≤2}.…………(3分)
≤2}.…………(3分)
(2)∵![]() ,
,![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
即对任意![]() ,恒有
,恒有![]() .…………(6分)
.…………(6分)
(3)![]() ,
,![]() ,
,![]() ,
,
![]() ,……(8分)
,……(8分)
一般地,![]() (
(![]()
![]() ).
).![]()
![]() …………(10分)
…………(10分)
(4)由(1)知,![]() ,∴
,∴![]() .则
.则![]() .∴
.∴![]() .
.
由(2)知,对![]() ,或1,或2,恒有
,或1,或2,恒有![]() ,∴
,∴![]() .则0,1,2
.则0,1,2![]() .
.
由(3)知,对![]() ,
,![]() ,
,![]() ,
,![]() ,恒有
,恒有![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
综上所述,![]() ,0,1,2,
,0,1,2,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .∴
.∴![]() 中至少含有8个元素.…………(16分)
中至少含有8个元素.…………(16分)
