第Ⅱ卷（非选择题，共100分）
二、填空题：（本大题共4小题，每小题5分，共20分，请把答案填在题中横线上）
11. 一台机器生产某种产品，如果生产出一件甲等品，可获利５０元，生产出一件乙等品，可获利３０元，生产出一件次等品，要赔２０元．已知这台机器生产出甲等品、乙等品、次等品的概率分别为0.6、0.3、0.1，则这台机器每生产一件这种产品平均预期可获利
元.
12. (x2+2x
– 4)5 = a0 +a1x+a2x2 + a3x3
+
+a10x10, 则x2的系数a2的值为___________.
13. 若函数
有极大值和极小值，则实数a的取值范围是
.
14. 下列函数：①y
= x3 – x; ②y=x+2
– x – 2; ③
;④y=
;⑤y
= x3 + sinx – 1. 其中既是奇函数，又在区间(0,1)上单调递增的为 .(写上相应的序号即可)
三、解答题：（本大题共6小题，共80分）
15.（满分13分）
已知
,
,若
是
的真子集,求实数m的取值范围.
16.（满分13分）
设函数
.
(1)求函数
的单调区间、极值;
(2)若当
时，恒有
，试确定a的取值范围.
17.（满分13分）
一种电路控制器在出厂时每四个一等品装成一箱，工人在装箱时不小心把两件二等品和两件一等品装入了一箱，为了找出该箱中的二等品，我们对该箱中的产品逐一取出进行测试.
(1)求前两次取出的都是二等品的概率；
(2)求第二次取出的是二等品的概率；
(3)用随机变量
表示两个二等品都被取出时共取出产品的件数，求的分布列及数学期望.
第 3页 共 4 页
18.（满分13分）
已知函数
,
），且
（1）若
，且函数的值域为
，求
表达式；
（2）在（1）的条件下，当
是单调函数，求实数k的取值范围；
（3）设
为偶函数，判断
能否大于0.
19.（满分14分）
已知数列
中，
且点
在直线
上.
(1)若函数
求证：
;
(2)设
表示数列
的前n项和.试问：是否存在关于
的整式
，使得
对于一切不小于2的自然数恒成立？若不存在，试说明理由; 若存在，写出的解析式，并加以证明.
20.（满分14分）
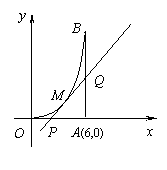
如图所示, 曲线段
是函数
0＜
＜6
的图象, 
轴于
, 曲线段上一点
处的切线
交轴于
,交线段
于
.
（1）试用
表示切线的方程;
（2）设
的面积为
,若函数在
上单调递减, 试求出
的最小值;
（3）
, 试求出点横坐标的取值范围.
第 4 页 共 4 页