 高 三 数 学 月 考 试 卷
高 三 数 学 月 考 试 卷
(命题人:张良 本试卷满分150分,考试时间120分钟)
一.选择题:(本大题共有12小题,每小题5分,共60分.)
1、设M={1,2,m2-3m-1},P={-1,3},M∩P={3},则m的值为 ( )
A.4 B.-1 C.1,-4 D.4,-1
2、 函数f (x)= sin x +cos x 的最小正周期是 ( )
A.![]() B.
B.![]()
![]() C.
C.![]() D.2
D.2![]()
3、 函数![]() 的反函数的解析表达式为 ( )
的反函数的解析表达式为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、若a与b的夹角为60°,b=2,(a+b)·(a-2b)=-2,则向量a的模是 ( )
A.2 B.5 C.3 D.6
5、x、y∈R,x2+y2=1,那么(1-xy)(1+xy)有 ( )
A.最小值![]() 和最大值1 B.最小值
和最大值1 B.最小值![]() 和最大值1 C.最小值
和最大值1 C.最小值![]() 无最大值 D.最小值
无最大值 D.最小值![]() 无最大值
无最大值
6、抛物线y=4![]() 上的一点M到焦点的距离为1,则点M的纵坐标是 ( )
上的一点M到焦点的距离为1,则点M的纵坐标是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 0
D. 0
7、把直线![]() 向左平移1个单位,再向下平移2个单位后,所得直线正好与圆x2+y2+2x-4y=0相切,则实数
向左平移1个单位,再向下平移2个单位后,所得直线正好与圆x2+y2+2x-4y=0相切,则实数![]() 的值为 ( )
的值为 ( )
A.3或13 B.-3或13 C.3或-13 D.-3或-13
8、不等式![]() ≥0的解集是 ( )
≥0的解集是 ( )
A.{xx≥-1} B.{xx≥1} C.{xx≥1或x=-1} D.{xx≥-1或x=1}
9、已知直线m、n与平面a、b,下列三个命题中真命题的个数是: ( )
①若m∥a,n∥a,则m∥n;②若m∥a,n⊥a,则n⊥m;③若m⊥a,m∥b,则a⊥b.
A.0 B.1 C.2 D.3
10、双曲线![]() -
-![]() =1(mn≠0)的离心率为2,则
=1(mn≠0)的离心率为2,则![]() 的值 ( )
的值 ( )
A.3 B.
![]() C.3或-
C.3或-![]() D.3或
D.3或![]()
11、设函数f(x)满足f(n+1)=![]() (n∈N*)且f(1)=2,则f(20)为 ( )
(n∈N*)且f(1)=2,则f(20)为 ( )
A.95 B.97 C.105 D.192
12、点P(-3,1)在椭圆![]() 的左准线上.过点P且方向为a=(2,-5)的光线,经直线
的左准线上.过点P且方向为a=(2,-5)的光线,经直线![]() =-2反射后通过椭圆的左焦点,则这个椭圆的离心率为 ( )
=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题:(本大题共6小题,每小题4分,共24分.)
13. 若f(x)=asin3x+btanx+1且f(1)=5,则f(-1)=_____________.
14.如果双曲线5x![]() 上的一点P到双曲线右焦点的距离是3,那么P点到左准线的距离是 __
上的一点P到双曲线右焦点的距离是3,那么P点到左准线的距离是 __
15. 已知向量![]() ,且A、B、C三点共线,则k=___________
,且A、B、C三点共线,则k=___________
16.设实数x、y满足
|
x-y+2≤0,
2x+y-5≤0,
17. 若a、b∈R,且a+b+3=ab,则ab的取值范围是____________.
18.在△ABC中,B(-2,0)、C(2,0)、A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下面给出了一些条件及方程,请你用线把左边△ABC满足的条件及相应的右边A点的轨迹方程连起来.(错一条连线得0分)
①△ABC周长为10 a y2=25
②△ABC面积为10 b x2+y2=4(y≠0)
③△ABC中,∠A=90° c ![]() +
+![]() =1(y≠0)
=1(y≠0)
三.解答题:(本大题共5小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19、已知函数![]() 求使
求使![]() 为正值的
为正值的![]() 的集合。
的集合。
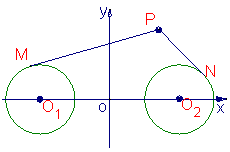
20、(本小题满分12分)如图,圆![]() 与圆
与圆![]() 的半径都是1,
的半径都是1,![]() ,过动点P分别作圆
,过动点P分别作圆![]() 、圆
、圆![]() 的切线PM、PN(M、N分别为切点),使得
的切线PM、PN(M、N分别为切点),使得![]() 。试建立适当的坐标系,并求动点P的轨迹方程。
。试建立适当的坐标系,并求动点P的轨迹方程。

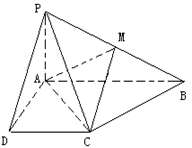 21、已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
21、已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,![]()
![]() ⊥底面ABCD,且PA=AD=DC=
⊥底面ABCD,且PA=AD=DC=![]() AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD; (Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小________________(本问只需写出答案,不需计算过程。)
22.已知函数![]() 、
、![]() 对任意实数
对任意实数![]() 、
、![]() 分别满足①
分别满足①![]() 且
且![]() ;②
;②![]() 且
且![]() ,(
,(![]() 为正整数)(1)求数列
为正整数)(1)求数列![]() 、
、![]() 的通项公式;(2)设
的通项公式;(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和。
项和。
23.设坐标平面上全部向量的集合为V,a=(a1,a2)为V的一个单位向量。已知从V到V的映射f由f(x)=-x+2(x·a)a(x∈V)确定。 (1)若x、y∈V,求证:f(x)·f(y)=x·y;
(2)对于x∈V,计算f[f(x)]-x;(3)设u=(1,0),v=(0,1),若f(u)=v,求a.
D、 C、 A、 C、 A、 B、 A、 B、 C、 D、 B、 A
-3、 14/3、 -2/3、 5、 (-∞,1]∪[9,+∞)、①→c ②→a ③→b
19、解:∵![]() ………………………………………………2分
………………………………………………2分
![]() …………………………………………………4分
…………………………………………………4分
![]()
![]() …………6分
…………6分
![]() …………………………8分
…………………………8分
![]() …………………………………………10分
…………………………………………10分
又![]() ∴
∴![]() ………………………12分
………………………12分
20、以![]()
![]() 的中点O为原点,
的中点O为原点,![]()
![]() 所在的直线为x轴,建立平面直角坐标系,则
所在的直线为x轴,建立平面直角坐标系,则![]() (-2,0),
(-2,0),![]() (2,0), (3分)
(2,0), (3分)
 由已知
由已知![]() ,得
,得![]()
![]()
因为两圆的半径均为1,所以
![]()
![]() (5分)
(5分)
设![]() ,则
,则![]() ,(7分)
,(7分)
即![]() ,
,
所以所求轨迹方程为![]()
![]() (或
(或![]() )
)![]() (12分)
(12分)
21、(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD. (2分)
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD. (4分)
又CD![]() 面PCD,∴面PAD⊥面PCD. (5分)
面PCD,∴面PAD⊥面PCD. (5分)
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角. (7分)
连结AE,可知AC=CB=BE=AE=![]() ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=![]() ,PB=
,PB=![]() , (9分)
, (9分)
![]()
![]() (11分)
(11分)
(Ⅲ)二面角为![]() (14分)
(14分)
22、解:(1)由![]() ,
,![]() ,知
,知![]() 成等比数列,
成等比数列,
![]() ……………………………………………………3分
……………………………………………………3分
由②中令![]() ,
,![]() ,得
,得![]() ,知
,知![]() 成等差数列,
成等差数列,
![]() ,即
,即![]() ……………………7分
……………………7分
(2)![]() ………………………………………10分
………………………………………10分
![]() ……………………14分
……………………14分
23、
(1)证明:f(x)·f(y)=[-x+2(x·a)a]·[-y+2(y·a)a] (2分)
=x·y-4(x·a)(y·a)+4(x·a)(y·a)a2=x·y. (4分)
(2)解:∵f[f(x)]=f[-x+2(x·a)a]
=-[-x+2(x·a)a]+2{[-x+2(x·a)a]·a}a (6分)
=x-2(x·a)a+2[-x·a+2(x·a)a2]a
=x-2(x·a)a+2(x·a)a=x,
∴f[f(x)]-x=0. (9分)
(3)解:由f(u)=v,得![]() (11分)
(11分)
解得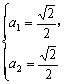 或
或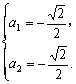 (13分)
(13分)
∴a=(![]() ,
,![]() )或a=(-
)或a=(-![]() ,-
,-![]() ). (14分)
). (14分)
