—、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | D | A | B | B | D | D | B | C | B | D |
二、填空题（每小题4分，共16分）
13． 148
14. i 15. 
16. 
(只要抛物线开口向上，对称轴为
就可以)
三、解答题（共74分）
17. （本题满分12分）
解： 
； 
；
∵
，∴
即
，解得 
或
当时，
符合题意
当 时，
不符合题意 故
18．（本题满分12分）
解：由于
是增函数，
等价于
①
（1）
当
时，
，
①式恒成立。
（2）
当
时，
，①式化为
，即
（3）
当
时，
，①式无解 综上
的取值范围是
19.（本题满分12分）
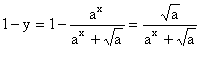
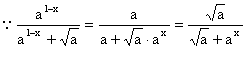解：(1)设M(x,y)是f(x)图象上任一点，则M关于P(
)的对称点为Ｍ′（１－ｘ，１－ｙ），
及
∴Ｍ′(1-x,1-y)亦在f(x)的图象上，
故函数f(x)的图象关于点P()对称. 。。。。。。。。。。。。。。6分
(2) 将f(n)、f(1-n)的表达式代入an的表达式，化简可得an＝ａｎ ，
猜a = 3, 即3ｎ＞ｎ２．下面用数学归纳法证明．
错误！未找到引用源。
；
显然成立；
错误！未找到引用源。假设n=k(k≥２)时，3ｋ＞ｋ２．
那么n=k+1时，3ｋ＋１=３·３ｋ＞３ｋ２，又3k２－（ｋ＋１）２＝２（ｋ－
）２－
>０
即3ｋ＋１＞（ｋ＋１）２（ｋ≥２，ｋ∈Ｎ*）
综上所述：不等式３ｎ＞ｎ２ 对一切正整数ｎ都成立。。。。。。。。。。。。。。。12分
20.（本小题满分12分）
解：（Ⅰ）至少有一名女同学的概率为
……3分
（Ⅱ）同学甲被选中的概率为
……6分
则同学甲被中且通过测试的概率为0.3×0.7=0.21……7分
（Ⅲ）根据题意，
的可能取值为0、1、2、3，
…………10分
|
的分布列为
（注：四个概率值正确，但未写分布列扣1分）
…………12分
21.（本小题满分12分）
解：（Ⅰ）f＇(x) =
=
，
∵f(x)在[－1，1]上是增函数，∴f＇(x)≥0对x∈[－1，1]恒成立，
即x2－ax－2≤0对x∈[－1，1]恒成立. ① ， 设
(x)=x2－ax－2，
方法一：
(1)=1－a－2≤0，
① 
－1≤a≤1，
(－1)=1+a－2≤0.
∵对x∈[－1，1]，f(x)是连续函数，且只有当a=1时，f＇(-1)=0以及当a=－1时，f＇(1)=0
∴A={a－1≤a≤1}.
方法二：
≥0，
<0，
①
或
(－1)=1+a－2≤0
(1)=1－a－2≤0
0≤a≤1
或 －1≤a≤0
－1≤a≤1.
∵对x∈[－1，1]，f(x)是连续函数，且只有当a=1时，f＇(－1)=0以及当a=-1时，f＇(1)=0
∴A={a－1≤a≤1}.………………………………6分
（Ⅱ）由
=
，得x2－ax－2=0， ∵△=a2+8>0
∴x1，x2是方程x2－ax－2=0的两非零实根，
x1+x2=a，
∴ 从而x1－x2=
=
.
x1x2=－2，
∵－1≤a≤1，∴x1-x2=≤3.
要使不等式m2+tm+1≥x1－x2对任意a∈A及t∈[－1，1]恒成立，
当且仅当m2+tm+1≥3对任意t∈[－1，1]恒成立，
即m2+tm－2≥0对任意t∈[－1，1]恒成立. ②
设g(t)=m2+tm－2 = mt+(m2－2)，
方法一：
g(－1)=m2－m－2≥0，
②
m≥2或m≤－2.
g(1)=m2+m－2≥0，
所以，存在实数m，使不等式m2+tm+1≥x1－x2对任意a∈A及t∈[－1，1]恒成立，
其取值范围是{mm≥2，或m≤－2}.
方法二：当m=0时，②显然不成立； 当m≠0时，
m>0，
m<0，
② 或
m≥2或m≤－2.
g(－1)=m2－m－2≥0 g(1)=m2+m－2≥0
所以，存在实数m，使不等式m2+tm+1≥x1－x2对任意a∈A及t∈[-1，1]恒成立，其取值范围是{mm≥2，或m≤－2}. ………………………………12分
22．（本小题满分14分）
解：（Ⅰ）证明：
∴ 结论成立 ……………………………………3分
（Ⅱ）证明：
当
即
…………6分
（Ⅲ）解：
（1）当
如果
即
时，则函数在
上单调递增
如果
当
时，
最小值不存在…………………………10分
（2）当
如果
即
时， 
如果
综上：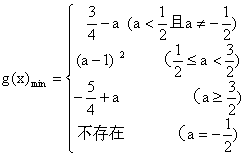
…………………………14分