商丘市回民高级中学高三第二次月考
数学试题(理)命题人 :赵后振 2005.10.10
—、选择题(每小题5分,共60分)
1.设集合![]() ,
, ![]() , 则A∩B=
, 则A∩B=
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为
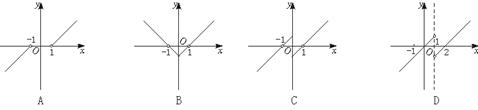
3.命题p:若a、b∈R,则a+b>1是a+b>1的充分而不必要条件;命题q:函数y=![]() 的定义域是(-∞,-1
的定义域是(-∞,-1![]() ∪[3,+∞
∪[3,+∞![]() ,则
,则
(A)“p或q”为假 (B)“p且q”为真 (C) p真q假 (D) p假q真
4. 函数![]() 的单调递增区间为
的单调递增区间为![]() ,那么实数a的取值范围是
,那么实数a的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、设![]() 是可导函数,且
是可导函数,且![]()
A.![]() B.-1 C.0 D.-2
B.-1 C.0 D.-2
6、已知实数a, b满足等式![]() 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b 其中不可能成立的关系式有
 A.1个 B.2个 C.3个 D.4个
A.1个 B.2个 C.3个 D.4个
7 、![]() 是
是![]() 的导函数,
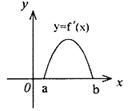
的导函数,![]() 的图象如图所示,
的图象如图所示,
则![]() 的图象只可能是
的图象只可能是
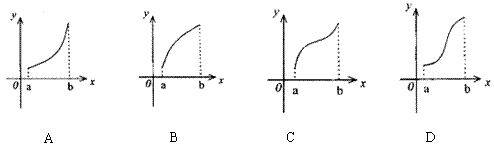 |
8、函数y=f(x)的周期是2,当-1![]() x
x![]() 1时f(x)=x
1时f(x)=x![]() 则
则![]() 与
与![]() 的图象的交点个
的图象的交点个
A.1 B.2 C . 3 D.4
9、设f(x)=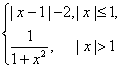 ,则f[f(
,则f[f(![]() )]= ( )
)]= ( )
A.![]() B.
B.![]() C.-
C.-![]() D.
D. ![]()
10、设![]() 、
、![]() 在[a,b]上可导,且
在[a,b]上可导,且![]() ,则当
,则当![]() 时,有 ( )
时,有 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11、. 已知函数![]() 的定义域为R,它的反函数为
的定义域为R,它的反函数为![]() ,如果
,如果![]() 与
与![]() 互为反函数且
互为反函数且![]() 。(
。(![]() 为非零常数)则
为非零常数)则![]() 的值为 ( )
的值为 ( )
A.![]() B.0
C.
B.0
C.![]() D.
D.![]()
12、已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如下图所示,则不等式![]() >0的解集为
>0的解集为
A.(-![]() ,0)∪(
,0)∪(![]() ,π) B.(-π,-
,π) B.(-π,-![]() )∪(
)∪(![]() ,π)
,π)
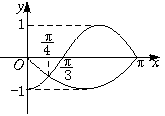 C.(-
C.(-![]() ,0)∪(
,0)∪(![]() ,π) D.(-π,-
,π) D.(-π,-![]() )∪(0,
)∪(0,![]() )
)
商丘市回民高级中学高三第二次月考
数学试题(理)(答题卡)
—、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题(每小题4分,共16分)
13.某校有高中生1200人,初中生900人,老师120人,现用分层抽样的方法从所有师生中, 抽取一个容量为![]() 的样本;已知从初中生中抽取人数为60人,那么
的样本;已知从初中生中抽取人数为60人,那么![]() =______________
=______________
14、![]() _________
_________
15、设函数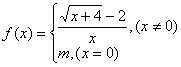 在点
在点![]() 处连续,则
处连续,则![]() =
=
16、老师给一个函数![]() ,四个学生甲、乙、丙、丁各指出这个函数的一个性质,
,四个学生甲、乙、丙、丁各指出这个函数的一个性质,
甲:对于![]() ;乙:在
;乙:在![]() 上函数递减;丙:在
上函数递减;丙:在![]() 上函数递增;丁:
上函数递增;丁:![]() 不是函数的最小值.如果其中恰有三个人说的正确,请写出一个这样的函数
.
不是函数的最小值.如果其中恰有三个人说的正确,请写出一个这样的函数
.
三、解答题(共74分)
17. (本题满分12分)已知集合![]() 集合
集合![]() 满足
满足![]() ,求实数
,求实数![]() 的值。
的值。
| 座号 |
18.(本题满分12分)
设函数![]() 的取值范围.
的取值范围.
19.(本题满分12分) 已知函数f(x)=![]() (a>0,a≠1).
(a>0,a≠1).
(1) 证明函数f(x)的图象关于点P (![]() )对称.
)对称.
(2) 令an=![]() ,对一切正整数n,先猜想使a n >n2成立的最小正整数a,并证明之.
,对一切正整数n,先猜想使a n >n2成立的最小正整数a,并证明之.
20.(本小题满分12分)从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,每位同学通过测试的概率为0.7,试求:
(Ⅰ)选出的三位同学中至少有一名女同学的概率;
(Ⅱ)选出的三位同学中同学甲被选中并且通过测试的概率;
(Ⅲ)设选出的三位同学中男同学的人数为![]() ,求
,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
21.(本小题满分12分)已知f(x)=![]() (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A ;
(Ⅱ)设关于x的方程f(x)=![]() 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等
式m2+tm+1≥x1-x2对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;
若不存在,请说明理由.
22.(本小题满分14分)
已知函数:![]()
(Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立.
(Ⅱ)当f(x)的定义域为[a+![]() ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(Ⅲ)设函数g(x) = x2+ (x-a) f(x) ,求g(x) 的最小值 .