湖 南 师 大 附 中

2005—2006学年度高三年级月考试题

数学（理科）

说明：本卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.考试时间120分钟，满分150分.

第Ⅰ卷（选择题　共50分）

一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中有且只有一项是符合题目要求的.

1．若复数的纯虚数，则　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　 B．　　 C．a=0　　　　　　　　　　D．a=2或a=0

2．若是正数的充要条件是　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　 B．　　　　　　　　 C．　　　　　　　 D．

3．设全集I=R，则集合

　 等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．C_IP　　　　　　　　　　 B．C_IQ　　　　　　　　　　 C．　　　　　　　　　　　 D．（C_IP）∪（C_IQ）

4．已知随机变量的值分别是　　　　　　　 （　　）

　　　 A．15与0.8　　　　　　 B．16与0.8　　　　　　 C．20与0.4　　　　　　 D．12与0.6

5．在等差数列{a_n}中，若a₂+ a₆+ a₁₆为一个确定的常数，则下列各个和中也为确定的常数的是　　　　　　　　　　　 （　　）

　　　 A．S₈ B．S₁₀ C．S₁₅ D．S₁₇

6．已知实数的运动轨迹是（　　）

　　　 A．抛物线　　　　　　　 B．双曲线　　　　　　　　C．椭圆　　　　　　　　　 D．圆

7．已知f(x)是奇函数，且当x>0时，的解析式是（　　）

　　　 A．　　　　　B．　　　　　　 C．　　　　　D．

8．设函数f(x)是可导函数，并且　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．－2　　　　　　　　　　 C．0　　　　　　　　　　　　D．－1

9．设函数的图象向左平移2个单位，再关于x轴对称后，所对应的函数的反函数是　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　 D．

10．给出下列4个命题：

　　　 ①若sin2A=sin2B，则△ABC是等腰三角形；

　　　 ②若sinA=cosB，则△ABC是直角三角形；

　　　 ③若cosAcosBcosC<0，则△ABC是钝角三角形；

　　　 ④若cos(A－B)cos(B－C)cos(C－A)=1，则△ABC是等边三角形.

　　其中正确的命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①③　　　　　　　　　 B．③④　　　　　　　　　 C．①④　　　　　　　　　 D．②③

第Ⅱ卷（非选择题　共100分）

二、填空题：本大题共5小题，每小题4分，共20分.

11．函数的定义域为　　　　　　　 .

12．已知则函数的解析式是=　　　　　　 .

13．已知函数　　　 .

14．设向量，则　　　　　　  .

15．求值：　　　　　　 .

三、解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.

16．（12分）已知为锐角，且

　　的值.

17．（12分）已知双曲线，左、右焦点分别为F₁、F₂，左准线为l，试推断在双曲线上的左支上是否存在点P，使得PF₁是点P到l的距离d与PF₂的等比中项？若存在，请求出点P的坐标；若不存在，请说明理由.

18．（14分）一袋中装有大小相同的8个小球，其中5个红球，3个黑球，现从中随机摸出3个球.

　 （Ⅰ）求至少摸到一个红球的概率；

　 （Ⅱ）求摸到黑球个数ξ的概率分布和数学期望.

19．（14分）在三棱锥P—ABC中，底面△ABC是以B为直角顶点的等腰直角三角形，点P在底面ABC上的射影H在线段AC上且靠近C点，AC=4，，PB和底面所成角为45°.

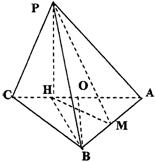
　 （Ⅰ）求点P到底面ABC的距离.

　 （Ⅱ）求二面角P—AB—C的正切值.

20．（14分）已知函数的切线方程为y=3x+1.

　 （Ⅰ）若函数处有极值，求的表达式；

　 （Ⅱ）在（Ⅰ）的条件下，求函数在[－3，1]上的最大值；

　 （Ⅲ）若函数在区间[－2，1]上单调递增，求实数b的取值范围.

21．（14分）已知数列{a_n}满足：

　 （Ⅰ）求数列{a_n}的通项公式；

　 （Ⅱ）求和；

　 （Ⅲ）设，若存在整数m，使对任意n∈N*，均有成立，求m的最大值.

高三数学（文）参考答案

一、选择题：

1.C  2.D　3.B　4.A  5.C　6.A　7.B  8.D　9.C　10.B

二、填空题

11．（－1，0）　12．　 13．2　　14．　 15．2

① ②

三、解答题：

16．解：由

∵

①÷②　　即  …………6分

又∵，∴

∴.　…………10分

∴　…………12分

17．设在左支上存在P点使PF₁²=PF₂·d，则

又　①　…………4分

又PF₂－PF₁=2a  ②

由①、②得　…………8分

因在△PF₁F₂中有　PF₁+PF₂≥2c，∴ ③　…………10分

利用代入③得

矛盾.

∴符合条件的点P不存在.　…………12分

18．（1）至少摸到一个红球的概率　　…………4分

　 （2）ξ表示摸到黑球个数，则

；　…………6分

. …………8分

∴摸到黑球个数ξ的概率分布为：

ξ	0	1	2	3
P

∴Eξ=　 …………14分

19．（1）∵P在底面ABC上的射影H在线段AC上，过P作PH⊥底面ABC，则H在AC上且靠近C点，∴面PAC⊥面ABC　…………2分

在等腰Rt△ABC中，连结BH取AC中点O，连BO.

设PH=h，由已知∠PBH=45°，则BH=h. …………4分

在△OHB中BO⊥AC，OB=

在Rt△PAH中，PA²=HA²+PH².

∴

∴P到底面ABC之距离为 ………7分

（2）在是CO中点.……9分

在△ABC中，过点H作HM⊥AB于垂足为M，连PM.

则∠PMH为二面角P—AB—C　…………12分

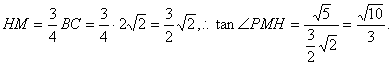∵ …………14分

20．（1）由

过的切线方程为：

 …………2分

① ②

而过

故　　 

∵　③

由①②③得　a=2，b=－4，c=5.　　

∴　 ………………5分

（2）

当

　…………8分

又在[－3，1]上最大值是13.　…………9分

（3）y=f(x)在[－2，1]上单调递增，又由①知2a+b=0.

依题意在[－2，1]上恒有≥0，即 ……10分

①当；

②当；

③当　…………13分

综上所述，参数b的取值范围是　…………14分

21．（1）∵

∴数列{a_n}成等差数列.　………………2分

由　……4分

（2）

　　

　　　…………9分

（3）∵　…………10分

∴

　　

　　 =　 …………11分

∴

∴{T_n}是递增数列.　∴是T_n的最小值. …………13分

由　 ∴满足条件的最大整数m=7　…………14分