荆州市 2006届高中毕业班质量检查(I)
数 学 (理工农医类)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A)·(B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率
![]()
第I卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B铅笔把第Ⅱ卷上端答题卡上对应题目的答案标号涂黑。多涂、不涂或涂错均得0分。
1. 设A、B为两个非空实数集合,定义集合A·B={a·b}a∈A,b∈B},若A={1,2,4},B={2,4,5},则A·B中元素的个数是
A.6 B.7 C.8 D.9
2.“a≤0”是“函数y=x2-2ax-3”在[0,1]上是单调函数”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知函数f(x)是定义在R上的偶函数,并且在(0,+∞)上是单调函数,若f(0)=-2,f(1)=0,使得f(x)<0的x的取值范围是
A.(- ∞,1) B.(1,+ ∞)
C.( - ∞,-1)∪(1,+ ∞) D.(-1,1)
4.在复平面内,复数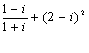 对应的点位于
对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.设f--!(x)是函数f(x)=ax-a-x(0<a<1=的反函数,则使f--1(x)< 1成立的x的取值范围是
A. (- ∞, ![]() )
B. (
)
B. (![]() ,+ ∞)
,+ ∞)
C.( ![]() ,a)
D.[a, + ∞)
,a)
D.[a, + ∞)
6.函数f(x)=x3-6ax+3a在(0,1)内有极小值,则
A.0<a<1 B.a<1
C. a>0
D. 0<a<![]()
7.已知tan(![]() )=
)=![]() ,则
,则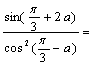
A. ![]() B.
B.
![]() C.
1
D.2
C.
1
D.2
8.在各项都为正数的等比数列{an}中,首项a1=2,则a3+a4+a5=
A. 34 B. 56 C. 72 D. 158
9.
当![]() ∈(0,
∈(0, ![]() ) 时,函数f(x)=
) 时,函数f(x)= ![]() 最小值是
最小值是
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
![]()
10.函数f(x)= 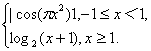 若
若![]() ,则m的所有可能值为
,则m的所有可能值为
A.1,-1 B. 1,0,-1
C.![]()
![]() D. 1,
D. 1, ![]()
![]()
11.在f(x)=sinx,f(x)=2x,f(x)=2x+1,f(x)=log2x,f(x)=x2这五个函数中,四个正实数x1,x2, ![]() ,
,![]() 满足x1≠x2,
满足x1≠x2,![]() ≠
≠![]() ,则当
,则当![]() 时,使
时,使![]() 恒成立的函数的个数是
恒成立的函数的个数是
A.1个 B.2个 C.3个 D.4个
12.已知函数![]() 与函数
与函数![]() 的单调区间相同且相同区间上单调性也相同,其中
的单调区间相同且相同区间上单调性也相同,其中![]() 且
且![]() ,若
,若![]() 有且仅有两个实数解,则实数
有且仅有两个实数解,则实数![]() 和
和![]() 的取值范围分别是
的取值范围分别是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
荆州市2006届高中毕业班质量检查(I)
数 学(理工农医类)
第II卷 (非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13. 数列![]() 满足
满足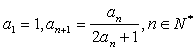 ,则数列
,则数列![]() 的通项公式是
的通项公式是![]() .
.
14. 设函数![]() 图象关于点(1,3)对称,且在反函数
图象关于点(1,3)对称,且在反函数![]() ,则
,则![]() .
.
15.设![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]() ,则
,则![]() .
.
16. 若函数![]()
![]() 在区间
在区间 ![]() 内单调递增,则
内单调递增,则![]() 的取值范围是
.
的取值范围是
.
三、解答题:本大题共6小题,共74分,解答题写出文字说明、证明过程或演算步骤.
17. (本小题满分12分)
已知函数![]() 的值域是[0 ,2].
的值域是[0 ,2].
(1) 求实数![]() 和
和![]() 的值;
的值;
(2) 设![]() ,求
,求![]() 的值.
的值.
18. (本小题满分12分)
一台设备的正常运转由三个部件控制,在设备运转过程中,各部件正常工作的概率分别是0.9,0.8,0.7,只要有一个部件正常工作,这台设备就能正常运转,假设各部件的状态相互独立,用![]() 表示发生故障的部件数.
表示发生故障的部件数.
(1) 求这台设备正常运转的概率.
(2) 求![]() 的概率分布和数学期望.
的概率分布和数学期望.
19. (本小题满分12分)
定义在R上的函数![]() 满足
满足![]() ,当
,当![]() 时,
时, ![]() =
=![]() .
.
(1) 求![]() 在区间[2,6]上的解析式.
在区间[2,6]上的解析式.
(2) 比较![]() 与
与![]() 的大小.
的大小.
20. (本小题满分12分)
已知![]()
(1) 若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2) 求![]() .
.
21.(本小题满分12分)
已知函数![]() .
.
(1) 求![]() 的单调区间和值域;
的单调区间和值域;
(2) 若函数![]() 在区间 [0,1] 上单调递减,设函数
在区间 [0,1] 上单调递减,设函数![]() 和
和![]() 在 [0,1] 上的值域分别为
在 [0,1] 上的值域分别为 ![]() 和
和![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
22.(本小题满分12分)
已知函数![]() In
In![]() .
.
(1) 当![]() 时,
时,![]() 是增函数,求实数
是增函数,求实数![]() 的取值范围;
的取值范围;
(2) 若![]() =0,数列
=0,数列![]() 满足
满足![]() ,证明:对一切
,证明:对一切![]() ,有
,有![]()
荆州市2006届高中毕业班质量检查(I)
数学试量(理)参考答案及说明
一、BADDB DABAB AA
二、13. ![]() 14. -1 15.0 16.
14. -1 15.0 16.![]()
三、17.解:(1)![]() =
=![]()
=![]() (4分)
(4分)
![]()
![]()
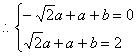
![]()
![]() (8分)
(8分)
(2)由(1)知![]()
![]()
![]()
![]()
![]()
![]()
![]() (12分)
(12分)
18.解:用![]() 表示第i个部件正常工作的事件,(i=1,2,3)
表示第i个部件正常工作的事件,(i=1,2,3)
则P(A1)=0,9 P(A2)=0.8 P(A3) =0.7
(1这台设备正常运转的概率P=1-P![]()
=![]() (4分)
(4分)
(2)P![]() =
=![]()
=0.9×0.8×0.7=0.504
![]()
=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398
![]()
=0.1×0.2×0.7+0.9×0.2×0.3+0.1×0.8×0.3=0.092
![]() (8分)
(8分)
![]()
|
| 0 | 1 | 2 |
| ||
| P | 0.504 | 0.398 | 0.092 | 0.006 |
![]()
=0.6 (12分)
19.解:(1)![]()
![]() (2分)
(2分)
![]()
![]()
![]() (4分)
(4分)
![]()
又![]()
![]()
![]()
![]() (6分)
(6分)
(2)由(1)知![]()
![]() =30
=30
![]()
![]()
![]() f ( log34+4) =
f ( log34+4) = ![]()
![]() (8分)
(8分)
又![]()
![]() (10分)
(10分)
![]()
![]()
![]() (12分)
(12分)
20.解:(1)当x=y时,![]() ,这时数列
,这时数列 ![]() 的前n项和Sn=2x+3x2+4x3+…+nxn-1+(n+1)xn ①
(2分)
的前n项和Sn=2x+3x2+4x3+…+nxn-1+(n+1)xn ①
(2分)
①式两边同乖以x,得
xSn =2x2 +3x3+4x4+…nxn + (n+1) xn+1 ②
①式减去②式,得
(1-x)Sn=2x + x2 + x3 +…+xn-(n+1) xn+1
若x≠1
![]()
![]() (4分)
(4分)
若x=1,
![]() (6分)
(6分)
(2)当x=y时,由(1),![]() =(n+1)xn,则
=(n+1)xn,则
![]()
![]() =
=![]()
![]() =
=![]()
![]() =
=![]() (8分)
(8分)
当x≠y时,
![]()
![]()
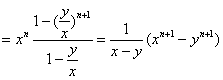 (10分)
(10分)
此时,![]()
若x > y > 0,则
![]()
![]() =
=![]()
![]() =
=![]()
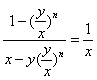
若 y > x > 0,则
![]()
![]() =
=![]()
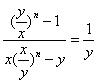 (12分)
(12分)
21.解:(1)![]()
![]()
当![]() ,解得
,解得![]() (4分)
(4分)
当x变化时,![]() 的变化情况如下表;
的变化情况如下表;
| x | 0 |
|
|
| 1 |
|
| - | 0 | + | ||
|
|
| ↘ | - 4 | ↗ |
|
所以,当![]()
![]() (8分)
(8分)
(2)对函数g(x)求导 ![]() 求导
求导![]() =3(x2-a2)
=3(x2-a2)
![]() g(x)在 [0,1] 上单调递减
g(x)在 [0,1] 上单调递减
![]()
![]() (8分)
(8分)
又g(x)在 [0,1]上是减函数
![]()
即![]()
而A![]() B
B
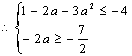
解得 ![]() (10分)
(10分)
又![]() (12分)
(12分)
22.解:(1)![]()
则![]() (2分)
(2分)
![]()
![]()
即![]() 上恒成立
上恒成立
![]() 时恒成立
时恒成立
![]()
![]()
![]()
![]()
![]() (6分)
(6分)
(2)![]()
由题设知 当n= 1时,![]()
假设 n=k 时,![]()
![]()
![]()
![]() 在区间(0,1)上是单调递增函数
在区间(0,1)上是单调递增函数
又![]()
![]()
即In2![]() <1
<1 ![]()
![]() ,都有0<
,都有0<![]() <1
(12分)
<1
(12分)
![]() 0<
0<![]() <1
<1
![]()
![]()
![]()
综上,对一切![]() ,有
,有![]() (14分)
(14分)
注:解答题若有其它解法,只要思路清晰,方法正确,均可酌情给分。