江苏省盐城市2005-2006学年度第一学期高三年级质量检测

数 学 试 题

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。考试时间120分钟。

第Ⅰ卷（选择题,共60分）

一 、选择题（每小题5分，共60分）

1．已知集合M={0,1,2}，N={xx=2a,a∈M},则集合M∩N=

A.{0}　　　　　　　 B.{0,1}　　　　　 C.{1,2}　　　　　  D.{0,2}

txjy

2．计算机的成本不断降低，若每隔3年计算机价格降低，现在价格为8100元的计算机，9年后的价格可降为

　 A．2400元　　　  B.900元　　　　  C.300元　　　　　 D.3600元

txjy

3．已知函数f(x)=lg,若f(a)=b,则f(-a)=

　 A.-b　　　　　　  B.b　　　　　　　 C.　　　　　　  D.-

txjy

4．数列1,，，…，的前项和为

　 A．　　　　　 B.　　　　　　 C.　　　　　　 D.

txjy

5．要得到函数y=cosx的图象，只需将函数y=sin (2x+)的图象上所有的点的

A．横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度

B．横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度

C．横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度

D．横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度

txjy

6．在区间［100,200］上的正整数中,被3除余2的数的个数是

　 A.32　　　　　　  B.33　　　　　　　　  C.34　　　　　　 D.35

txjy

7．已知函数f (x)=2-3x-(x≥1)，则有

　 A．有最大值2-4　　　　　　　　　　　 B.有最小值2-4

　 C．有最大值-5　　　　　　　　　　　　　　 D.有最小值-5

txjy

8．不等式2x+5≥7成立的一个必要不充分条件是

　 A．x≥1　　　　　　 b.x≤-6　　　　　　  C.x≥1或x≤-6　　　　 D.x≠0

9．函数y=-x(2+x)(x≥0)的反函数的定义域为

　 A．（+∞,1］　　　　 B.(0,1］　　　　　　　　　 C. ［0,+∞)　　　　　　　 D.(+∞,0］

10.设a＞0, b＞0,则以下不等式中不恒成立的是

A．(a+b)(≥4　　　　　　　　　　　　  B．a≥2a

C．a＞2a　　　　　　　　　　　　　　 D． ≥

11.若不等式x- log x＜0在区间（0,）内恒成立，则实数m的取值范围是

　　A．≤m＜1　　　　　 B.0＜m≤　　　　C.0＜m＜　　　　　　  D. m≥

12.设f(x)=2sin (x+)，若对任意x∈R都有f (x)≤f (x) ≤f (x)成立，则x-x的最小值是

A．4　　　　　　　　　 B.2　　　　　　　　 C.1　　　　　　  D.

第Ⅱ卷（非选择题,共90分）

二、填空题（每小题4分，共24分）

13.函数y=的最小正周期是_________________________.

14.若不等式＞0的解集为{x-3＜x＜ -1或x＞2},则=____________.

15.已知向量满足=2,=1, -=2,则 +=______________.

16.我们知道反比例函数y=图象的对称中心为O（0,0），那么函数y=图象的对称中心坐标为____________________.

17.在锐角三角形ABC中，∠BAC=45°,AD为BC边上的高，且BD=2,DC=3，则三角形ABC的面积是___________.

18.若数列{}，(n∈N)是等差数列,则有数列b=(n∈N)也是等差数列，类比上述性质，相应地：若数列{c}是等比数列,且c＞0(n∈N),则有d=______________ (n∈N)也是等比数列.

三、解答题（满分66分）

19.(本题满分12分)

　 设集合A={yy=·4-4·2+9　x∈［0,3］},B={y(y-)( y--1)≥0}，若A∩B=Φ,求实数的取值范围.

20.(本题满分12分)

　　已知S是等比数列{}的前n项和，S,S,S成等差数列.

（1）求数列{}的公比q;

（2）试问,的等差中项是数列{}中的第几项？并说明理由.

21.(本题满分14分)

已知函数f(x)=x-2+

（1）求f(x)的定义域；

（2）判断f(x)的奇偶数，并说明理由；

（3）求f(x)的值域.

22. (本题满分14分)

已知向量=（cos）, =(cos,x∈［］,

（1）求·及+；

（2）求函数f(x)= (∈R且≠0)的最小值.

23. (本题满分14分)

　　 定义在R上的函数f(x)满足：如果则任意x,x∈R，都有f()≤［f(x)，则称函数f(x)是R上的凹函数.

已知二次函数f(x)= x+x(∈R, ≠0).

（1）求证：当＞0时，函数f(x)是凹函数.

（2）如果x∈［0,1］时，f(x)≤1，试求实数的范围.

参考答案

一、　　　　　　 选择题（每小题5分，共60分）

1.D 2.A 3.A 4.B 5.C 6.C 7.A 8.D 9.D 10.B 11.A 12.C

二、　　　　　　 填空题（每小题4分，共24分）

13．2;14.-2;15.;16.(2,-1);17.15;18.

三、　　　　　　 解答题（满分66分）

19.解：y =(2)-4·2+9=(2-4) +1

∵x∈［0,3］ ∴2∈［1,8］∴A=［1,9］

∵+1＞　　∴B={yy≤或y≥+1}

∵A∩B=φ

∴　＜1

+1＞9

∴＜-2

20.解：（1）若q=1，则S=3,S=9,S=6₁不成等差数列

故q≠1,此时由S, S s成等差数列得

2 S= S+ S,2·

化简得：2q

所以q=-

(2)为第10项.

21．解：

（1）定义域为{x-2≤x≤2}

(2)因为f(-1)≠- f(1)且f(-1)≠f(1)，

所以f(x)既不是奇函数又不是偶函数.

（3）设x=2cosθ(0≤θ≤π),则y=2sin (θ+)-2，所以-4≤y≤2-2

即f(x)的值域为［-4,2-2］

22．解：（1）·=cos=cos(

∵+=(cos

又∵x∈［］　∴+=2cosx

(2) f(x)= =(cosx-)，

又∵x∈［］∴≤cosx≤

∵g(t)=t-在（t＞0）为增函数

∴当＞0时，cosx=时，f(x)取得最小值0,

当＜0时，cosx=时，f(x)取得最小值.

23.解：（1）对任意x＞0,

∴［f(x)+ f (x)］-2 f(［()］

=x≥0.

∴f(≤［f ］.　　 ∴函数f(x)是凹函数;

(2)由 f(x)≤1　　　　-1≤f(x) ≤1　　　　 -1≤+x≤1.(*)

当x=0时，∈R;当x∈(0,1］时，(*)即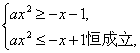

即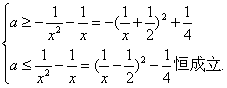

∵x∈(0,1］,∴≥1.

∴当=1时，-(+)-取得最大值是-2；当=1时，(-)-取得最小值是0.

∴-2 ≤≤0 ,结合≠0，得-2≤＜0.

综上，的范围是［-2,0).