江苏省苏州市部分重点中学2006届高三期中考试试卷
数 学 2005.11
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知平面向量![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.1 D.4
C.1 D.4
(2)已知集合![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)已知函数![]() ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
A.![]() 是周期为1的奇函数 B.
是周期为1的奇函数 B.![]() 是周期为2的偶函数
是周期为2的偶函数
C.![]() 是周期为1的非奇非偶函数 D.
是周期为1的非奇非偶函数 D.![]() 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
(4)设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于 ( )
等于 ( )
A.18 B.36 C.45 D.60
(5)函数![]() 的反函数 ( )
的反函数 ( )
A.在![]() 上单调递增 B.在
上单调递增 B.在![]() 上单调递减
上单调递减
C.在![]() 上单调递增 D.在
上单调递增 D.在![]() 上单调递减
上单调递减
(6)设![]() 均为非空集合,且满足
均为非空集合,且满足![]() ,则下列各式中错误的是 ( )
,则下列各式中错误的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(7)命题![]() :
:![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
命题![]() :在
:在![]() 中,如果
中,如果![]() ,那么
,那么![]() 为直角三角形.则 ( )
为直角三角形.则 ( )
A.“![]() 或
或![]() ”为假 B.“
”为假 B.“![]() 且
且![]() ”为真 C.
”为真 C.![]() 假
假![]() 真 D.
真 D.![]() 真
真![]() 假
假
(8)设函数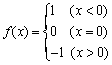 ,则当
,则当![]() 时,
时,![]() 的值应为 ( )
的值应为 ( )
A.![]() B.
B.![]() C.
C.![]() 中的较小数 D.
中的较小数 D.![]() 中的较大数
中的较大数
(9)函数![]()
![]() 的图象的大致形状是 ( )
的图象的大致形状是 ( )
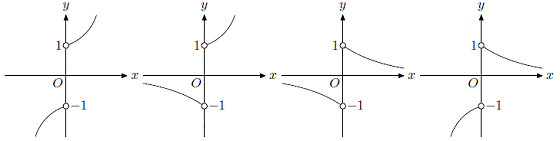
A B C D
(10)在![]() 中,
中,![]() ,则
,则![]() 边上的高为 ( )
边上的高为 ( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
(11)已知函数![]() 为奇函数,函数
为奇函数,函数![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() = ( )
= ( )
A.2 B.![]() C.4 D.
C.4 D.![]()
(12)为了稳定市场,确保农民增收,某农产品的市场收购价格![]() 与其前三个月的市场收购价格有关,且使
与其前三个月的市场收购价格有关,且使![]() 与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
则7月份该产品的市场收购价格应为 ( )
A.69元 B.70元 C.71元 D.72元
第Ⅱ卷(非选择题 共90分)
二.填空题:本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应的位置上.
(13) 若![]() ,则
,则![]() ▲ .
▲ .
(14) 函数![]() 在区间
在区间![]() 上的最大值为
▲ .
上的最大值为
▲ .
(15) 已知平面向量![]() ,若
,若![]() ,则实数
,则实数![]() ▲ .
▲ .
(16) 已知集合![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
▲ .
(17) 已知![]() 分别是关于
分别是关于![]() 的二次方程
的二次方程![]() 的两实根的等差中项和等比中项,则
的两实根的等差中项和等比中项,则![]() 满足的关系式为
▲ .
满足的关系式为
▲ .
(18) 若![]() 为
为![]() 的各位数字之和
的各位数字之和![]() .如:因为
.如:因为![]() ,所以
,所以![]() .记
.记![]() ,
,![]() ,……,
,……,![]() ,
,![]() ,则
,则![]() =
▲ .
=
▲ .
三.解答题:本大题共5小题,共66分.解答应写出文字说明、证明过程或演算步骤.
(19) (本小题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调减区间;
的单调减区间;
(Ⅱ)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(Ⅲ)若函数![]() 的图象按向量
的图象按向量![]()
![]() 平移后得到函数
平移后得到函数![]() 的图象,求实数
的图象,求实数![]() 的值.
的值.
(20) (本小题满分12分)
在![]() 中,
中,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 的面积最大时,求
的面积最大时,求![]() 的大小.
的大小.
(21) (本小题满分14分)
设函数![]() .
.
(Ⅰ)若![]() ,证明函数
,证明函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,并且
,并且![]() ;
;
(Ⅱ)若![]() ,且当
,且当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(22) (本小题满分14分)
某市电信宽带私人用户月收费标准如下表:
| 方案 | 类 别 | 基本费用 | 超时费用 |
| 甲 | 包月制 | 70元 | |
| 乙 | 有限包月制(限60小时) | 50元 | 0.05元/分钟(无上限) |
| 丙 | 有限包月制(限30小时) | 30元 | 0.05元/分钟(无上限) |
假定每月初可以和电信部门约定上网方案.
(Ⅰ)若某用户每月上网时间为66小时,应选择 ▲ 方案最合算;
(Ⅱ)王先生因工作需要在家上网,所在公司预测其一年内每月的上网时间![]() (小时)与月份
(小时)与月份![]() 的函数关系为
的函数关系为![]() .若公司能报销王先生全年上网费用,问公司最少会为此花费多少元?
.若公司能报销王先生全年上网费用,问公司最少会为此花费多少元?
(Ⅲ)一年后,因公司业务变化,王先生每月的上网时间![]() (小时)与月份
(小时)与月份![]() 的函数关系为
的函数关系为![]() .假设王先生退休前一直从事此项业务,公司在花费尽量少的前提下,除为其报销每月的基本费用外,对于所有的超时费用,公司考虑一次性给予补贴
.假设王先生退休前一直从事此项业务,公司在花费尽量少的前提下,除为其报销每月的基本费用外,对于所有的超时费用,公司考虑一次性给予补贴![]() 元,试确定最合理的
元,试确定最合理的![]() 的值,并说明理由.
的值,并说明理由.
(23) (本小题满分14分)
已知函数![]() ,并且
,并且![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在各项均不为零的数列![]() ,满足
,满足![]() (
(![]() 为数列
为数列![]() 的前
的前![]() 项和).若有,写出数列的一个通项公式
项和).若有,写出数列的一个通项公式![]() ,并说明满足条件的数列
,并说明满足条件的数列![]() 是否唯一确定;若无,请说明理由.
是否唯一确定;若无,请说明理由.
江苏省苏州市部分重点中学2006届高三期中考试试卷
数学参考答案及评分标准
说明:
1.本解答仅给出了一种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容对照评分标准制订相应的评分细则.
2. 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3. 解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4. 给分或扣分均以1分为单位.选择题和填空题不给中间分.
一.选择题:每小题5分,满分60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | A | B | B | C | D | C | D | C | D | A | B | C |
二.填空题:每小题4分,满分24分.
(13)![]() (14)3 (15)3或
(14)3 (15)3或![]()
(16)![]() (17)
(17)![]() (18)11
(18)11
三.解答题:
(19)本小题满分12分.
解:(Ⅰ)![]() ……………………………………………………………1分
……………………………………………………………1分
![]()
![]() .……………………………………………………………2分
.……………………………………………………………2分
令 ![]() ,…………………………………………3分
,…………………………………………3分
得 ![]() .
.
因此,函数![]() 的单调减区间为
的单调减区间为![]() .………………………5分
.………………………5分
(Ⅱ)当![]() 时,
时,![]() ,………………………………………………6分
,………………………………………………6分
∴ ![]() .……………………………………………………………7分
.……………………………………………………………7分
因此,函数![]() 的值域为
的值域为![]() .……………………………………………………8分
.……………………………………………………8分
(Ⅲ)函数![]() 的图象按向量
的图象按向量![]()
![]() 平移后得到的图象对应的函数是
平移后得到的图象对应的函数是![]() .……………………………………10分
.……………………………………10分
令 ![]() ,得
,得 ![]() .…………………………………12分
.…………………………………12分
(20)本小题满分12分.
解:(Ⅰ)由已知得
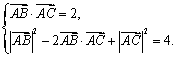 ……………………………………………………………3分
……………………………………………………………3分
因此,![]() .……………………………………………………………… 4分
.……………………………………………………………… 4分
(Ⅱ)![]() ,…………………………………………………………6分
,…………………………………………………………6分
![]()
![]()
![]()
![]() ………………………………………………………………8分
………………………………………………………………8分
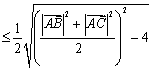
![]() .…………………………………………………10分
.…………………………………………………10分
(当且仅当![]() 时,取等号)…………………………………………11分
时,取等号)…………………………………………11分
当![]() 的面积取最大值
的面积取最大值![]() 时,
时,![]() ,
,![]() .………………12分
.………………12分
(21)本小题满分14分.
解:(Ⅰ)当![]() 时,
时,![]() .
.
![]() .……………………………………………………………1分
.……………………………………………………………1分
∵ ![]() ,
,
∴ 方程![]() 有两个不等的实数根
有两个不等的实数根![]() .…………………………………………3分
.…………………………………………3分
不妨设![]() ,则
,则 ![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴ ![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点.……………………………………4分
的极小值点.……………………………………4分
并且,![]() .
.
因此,函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,并且
,并且![]() (当且仅当
(当且仅当![]() 时取等号).…………………………………………………………………………………7分
时取等号).…………………………………………………………………………………7分
(Ⅱ)当![]() 时,
时,
![]() .
.
![]() .………………………………………………8分
.………………………………………………8分
①若![]() ,则
,则![]() 在
在![]() 上增函数,在
上增函数,在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
![]() 在
在![]() 上的最大值为
上的最大值为![]() 与
与![]() 中的较大者.
中的较大者.
而![]() ,
,![]() .
.
由![]() 在
在![]() 上恒成立,得
上恒成立,得
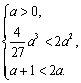 ……………………………………………………………………………9分
……………………………………………………………………………9分
即![]() .……………………………………………………………………………11分
.……………………………………………………………………………11分
②若![]() ,则
,则![]() 在
在![]() 上为增函数.
上为增函数.
![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
∵ ![]() ,∴
,∴ ![]() .
.
∴![]() .
.
因此,![]() 不可能.…………………………………………………………………13分
不可能.…………………………………………………………………13分
综上所述,![]() 的取值范围是
的取值范围是![]() .…………………………………………………14分
.…………………………………………………14分
(22)本小题满分14分.
解:(Ⅰ) 乙 .……………………………………………………………………………2分
(Ⅱ)当![]() 时,选择丙方案合算;
时,选择丙方案合算;
当![]() 时,由
时,由![]() ,得
,得![]() ,此时选择丙方案合算;
,此时选择丙方案合算;
当![]() 时,选择乙方案合算;
时,选择乙方案合算;
当![]() 时,由
时,由![]() ,得
,得![]() ,此时选择乙方案合算;
,此时选择乙方案合算;
当![]() 时,选择甲方案合算.
时,选择甲方案合算.
综上可得:当![]() ,选择丙方案合算;……………………………………3分
,选择丙方案合算;……………………………………3分
当![]() 时,选择乙方案合算;……………………………………………4分
时,选择乙方案合算;……………………………………………4分
当![]() 时,选择甲方案合算.……………………………………………5分
时,选择甲方案合算.……………………………………………5分
∵![]() ,∴
,∴![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,且每月上网时间逐月递增.
的等差数列,且每月上网时间逐月递增.
令![]() ,得
,得![]() .
.
∴前9个月选择乙方案,最后3个月选择甲方案上网花费最少.……………………7分
此时,一年的上网总费用为
![]()
![]()
![]() .
.
答:一年内公司最少会为王先生花费上网费741元.……………………………………9分
(Ⅲ)由![]() 知,
知,![]() ,且
,且![]() 是递减数列,
是递减数列,
∴选择丙方案合算.……………………………………………………………………10分
若上网![]() 个月,王先生的超时总费用为
个月,王先生的超时总费用为
![]() .……………………………………………13分
.……………………………………………13分
答:公司考虑一次性给予补贴![]() 元,最合理的
元,最合理的![]() 的值为45元.……………………14分
的值为45元.……………………14分
(23)本小题满分14分.
解:(Ⅰ)由![]() ,得
,得![]() .
.
由![]() ,
,![]() ,得
,得
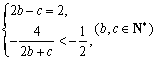 ,即
,即![]() .……………………………3分
.……………………………3分
解得 ![]() .
.
因此,![]() ,
,![]() .……………………………………………………………5分
.……………………………………………………………5分
(Ⅱ)由(Ⅰ)得![]() .当
.当![]() 且
且![]() 时,
时,![]() ,
,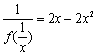 .
.
设存在各项均不为零的数列![]() ,满足
,满足![]() .则
.则
![]() ,即
,即![]() (
(![]() 且
且![]() ).…………………………6分
).…………………………6分
首先,当![]() 时,
时,![]() ;……………………………………………………7分
;……………………………………………………7分
由
![]() ,
,![]() ,得
,得
![]() ,即
,即
![]() .……………………………………………………………9分
.……………………………………………………………9分
若
![]() ,则由
,则由![]() ,得
,得![]() ,这与
,这与![]() 矛盾.………………………10分
矛盾.………………………10分
若
![]() ,则
,则 ![]() .
.
因此,![]() 是首项这
是首项这![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
通项公式为
![]() .
.
综上可得,存在数列![]() ,
,![]() 符合题中条件.…………………………………11分
符合题中条件.…………………………………11分
由上面的解答过程可知,数列![]() 只要满足条件
只要满足条件![]() 即可.
即可.
因此,可以数列一部分满足![]() ,另一部分满足
,另一部分满足![]() ,且保证
,且保证![]() 且
且![]() .
.
例如:数列 ![]() ;
;
数列 ![]()
因此,满足条件的数列不唯一.………………………………………………………14分
