北京朝阳02-03年上学期高二数学期末统一考试

（考试时间100分钟　得分100分）

一、选择题：本大题共10个小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后的括号内。

（1）不等式2^2x-1＜1的解集是　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A）（，1）　　　 （B）（0，）　　　（C）（，∞）　 （D）（-∞, ）

(2)“a+b＞2c”的一个充分条件是　　　　　　　　　　　　　　　　　　　　　  （　　）

（A）a＞c,或b＞c　　 (B)a＞c，且b＜c　　　(C)a＞c,且 b＞c　　(D)a＞c,且b＜c

(3)arcsin与arcsin的关系是　　　　　　　　　　　　　　　　　　　　　　  （　　）

（A）arcsin＜arcsin　　　　　 （B）arcsin＞arcsin

（C）arcsin＝arcsin　　　　　 （D）arcsin≥arcsin

（4）一条直线上顺次有A、B、C三点，且│AB│=2，│BC│=3，则C分有向线段的比为　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　（　　）

（A）- 　　　（B）- 　　　（C）　　  （D）

（5）下列函数中，最小值是4的是　　　　　　　　　　　　　　　　　　　  　（　　）

（A）y=x+　　　　　　　　　　　　 (B)=2

（C）y=sinx+4cscx,x∈(0，　　 （D）y=2(7^x+7^-x)

（6）圆x²+y²=1与曲线xy-y=0的交点个数是　　　　　　　　　　　　　　　　 （　　）

（A）1个　　 （B）2个　　 （C）3个　　　（D）4个

（7）不等式＜x+1的解集是M，│x+5│＞1的解集为N，则M与N的关系是

　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　（　　）

（A）MN　　　 （B）NM　　（C）M=N　　　　（D）M∩N=φ

（8）一个等差数列的前4项之和是40，最后4项之和是80，所有项之和为210，则这个数列共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　）

（A）12项　　 （B）14项　　（C）16项　　　（D）18项

（9）已知直线l₁：y=kx+（k＜0 ＝被圆x²+y²=4截得的弦长为，则l₁与直线l₂：y=（2+）x的夹角的大小是　　　　　　　　　　　　　　　　　　　　　（　　　）

（A）30°　　　（B）45°　　　（C）60°　　　 （D）75°

（10）已知数列｛a_n｝满足a₁=1,a_n+1=，则a₃₀=　　　　　　　　　　　　（　　　）

（A）100　　　 （B）88　　　 （C）　　　　 （D）

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题后横线上.

（11）在数列1，4，7，10，x，16.中，x的值是　　　　　　　 .

（12）已知点A（-1，-2），B（2，4），若直线ax+3y-5=0经过线段AB的中点，则a=　　　

（13）关于x的不等式（m²-4m+3）x²+2（m+1）x+1＞0对任意x∈R都成立，则实数m的范围是　　　　　　  .

（14）已知点P（x,y）是第一象限的点，且点P在直线3x+2y=6上运动，则使xy取最大值的点P的坐标为　　　　　　　  .

三、解答题：（本大题共6个小题，共44分.解答应写出文字说明，证明过程或演算步骤.）

（15）（本小题满分6分）

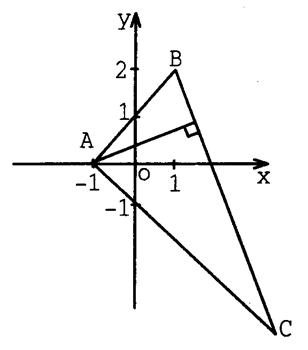
如图，ΔABC中，已知A（-1，0），B（1，2），点B关于y=0的对称点在AC边上，且BC边上的高所在的直线方程为x-2y+1=0.

（Ⅰ）求AC边所在直线的议程;

（Ⅱ）求点C的坐标.

（16）（本小题满分6分）

已知：a＞0，b＞0.

求证：≥a+b.

（17）（本小题满分6分）

解关于x的不等式log₂＞log₂(1+x)-log₂k（k是大于零的常数）.

（18）（本小题满分8分）

已知数列｛a_n｝中，S_n表示前n项和，如果a_n＞0, a_n+2=2.

求证数列｛a_n｝为等差数列.

(19)(本小题满分9分)

某公司一年生产某种产品m件,并且分若干批生产(每批生产产品件数相同),已知每生产一批产品需用原料费15000万元,每批生产需直接消耗的管理等费用S与该批生产产品的件数x的立方成正比,当生产的一批产品为5件时，S=1000万元.

（Ⅰ）求S关于x的函数表达式

（Ⅱ）每批生产产品多少件时，一年生产的总费用最低（精确到1件，≈）

（20）（本小题满分9分）

（重点校学生做，普通校学生选做）

已知点B是半圆x²+y²=1（y＞0）上的一个动点，点A的坐标为（2，0），ΔABC是以BC为斜边的等腰直角三角形，且顶点A、B、C按顺时针方向排列.求点C的轨方程.

（普通校学生做，重点校学生不做）

已知圆x²+y²=25上的两个定点A（0，5），B（3，4）和一个动点D.求以AB、AD为两邻边的平行四边形ABCD的顶点C的轨迹方程.