江苏省白蒲高级中学2005-2006年度高三模拟考试
数 学 试 卷
时间:120分钟 总分:150分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.设函数![]() 的定义域为集合M,集合N=
的定义域为集合M,集合N=![]() ,则
,则![]()
A.M B.N C.![]() D.
D.![]()
2.设非零向量![]() 、
、![]() 、
、![]() ,若
,若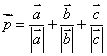 ,那么
,那么![]() 的取值范围为
的取值范围为
A.[0,1] B.[0,2] C.[0,3] D.[1,2]
3.甲、乙、丙、丁四名射击选手在选拨赛中所得的
| 甲 | 乙 | 丙 | 丁 | |
|
| 8 | 9 | 9 | 8 |
| S2 | 5.7 | 6.2 | 5.7 | 6.4 |
平均环数![]() 及其方差S2如下表所示,则选送参加
及其方差S2如下表所示,则选送参加
决赛的最佳人选是
A.甲 B.乙 C.丙 D.丁
4.若![]() 、
、![]() 为空间两条不同的直线,
为空间两条不同的直线,![]() 、
、![]() 为空间两个不同的平面,则
为空间两个不同的平面,则![]() 的一个充分条件是
的一个充分条件是
A.![]() 且
且![]() B.
B.![]() 且
且![]()
C.![]() 且
且![]() D.
D.![]() 且
且![]()
5.某班共有6个数学研究性学习小组,本学期初有其它班的3名同学准备加入到这6个小组中去,则这3名同学恰好有2人安排在同一个小组的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在斜三角形ABC中,![]() 且
且![]() ,则∠A的值为
,则∠A的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.我们把离心率为黄金比![]() 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设![]() (a>b>0)为“优美椭圆”,F、A分别是它的左焦点和右顶点,B是它短轴的一个端点,则∠ABF等于
(a>b>0)为“优美椭圆”,F、A分别是它的左焦点和右顶点,B是它短轴的一个端点,则∠ABF等于
A.60° B.75° C.90° D.120°
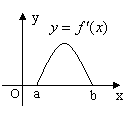
8.![]() 是
是![]() 的导函数,
的导函数,![]() 的图象如图所示,
的图象如图所示,
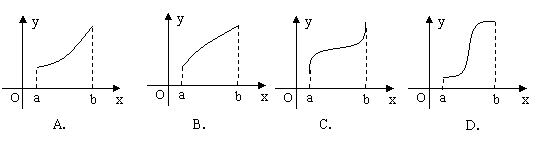
则![]() 的图象只可能是
的图象只可能是
| |
9.在1,2,3,4,5的排列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,中,满足
,中,满足 ![]() <
<![]() ,
,![]() >
>![]() ,
,![]() <
<![]() ,
,![]() >
>![]() 的排列个数是
的排列个数是
A.10 B.12 C.14 D.16
10.设函数![]() ,若关于
,若关于![]() 的方程
的方程![]()
恰有3个不同的实数解![]() ,则
,则![]() 等于( )
等于( )
A.0 B.lg2 C.lg4 D.l
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填写在答题卡相应位置上.
11.某住宅小区有居民2万户,从中随机抽取200户,调查是否安装宽带,调查结果如下表所示:
| 宽带 | 动迁户 | 原住户 |
| 已安装 | 60 | 35 |
| 未安装 | 45 | 60 |
则该小区已安装宽带的户数估计有 户
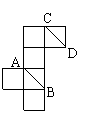 12.已知
12.已知![]() ,坐标原点O在直线AB上的射影为点C,则
,坐标原点O在直线AB上的射影为点C,则![]() =______
=______
13.右图是正方体的展开图,其中直线
AB与CD在原正方体中所成角的大小
是___________
14.已知点P(x,y)在曲线![]() 上运动,作PM垂直于x轴于M,则△POM(O为坐标原点)的周长的最小值为___________.
上运动,作PM垂直于x轴于M,则△POM(O为坐标原点)的周长的最小值为___________.
15.![]() =___________
=___________
16.函数![]() 是定义在无限集合D上的函数,关且满足对于任意的
是定义在无限集合D上的函数,关且满足对于任意的![]() ,
,
![]()
①若![]() 则
则![]() =
;
=
;
②试写出满足下面条件的一个函数![]() 存在
存在![]() ,使得由
,使得由![]() ,…,
,…,![]() ,…组成的集合有且仅有两个元素.这样的函数可以是
,…组成的集合有且仅有两个元素.这样的函数可以是![]() =
.
=
.
(只需写出一个满足条件的函数)
三、解答题:本大题共5小题,共70分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分) 已知![]() 的面积S满足
的面积S满足![]() ,且
,且![]() ,
,![]() 的夹角为
的夹角为![]() .
求:(1)
.
求:(1) ![]() 的取值范围;
的取值范围;
(2)函数![]() 的最小值.
的最小值.
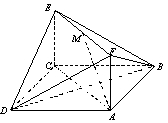 18.(本小题满分14分) 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
18.(本小题满分14分) 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证AM//平面BDE; (2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是 60°.
19.(本小题满分14分)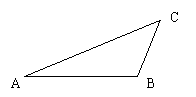
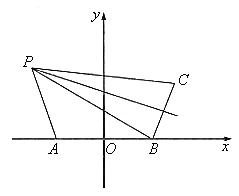
飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东300,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.
(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角;
(3)若信号从P点的正上方Q点处发出,则A、B
收到信号的时间差变大还是变小,并证明你的结论.
20.(本小题满分14分)
设![]() 、
、![]() 是函数
是函数![]() (a>0)的两个极值点,且
(a>0)的两个极值点,且![]() .
.
(I)证明:![]() ;
;
(II)证明:![]() .
.
21.(本小题满分16分)
设定义在R上的函数f(x)满足:①对任意的实数x,y∈R,有f(x+y)=f(x)·f(y);
②当x>0时,f(x)>1.数列{an}满足a1=f(0),且f(an+1)=![]() (n∈N*).
(n∈N*).
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)求数列{an}的通项an的表达式;
(Ⅲ)令![]() 是最接近
是最接近![]() ,
,
设Tn=![]() … +
… +![]() .
.
[答案]
17(1)![]() (2)3
(2)3
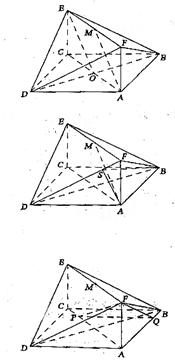 18.方法一
18.方法一
解: (1)记AC与BD的交点为O,连接OE,
∵O、M分别是AC、EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,∴AM∥OE。
∵![]() 平面BDE,
平面BDE,
![]() 平面BDE,∴AM∥平面BDE。
平面BDE,∴AM∥平面BDE。
(2)在平面AFD中过A作AS⊥DF于S,连结BS,
∵AB⊥AF, AB⊥AD, ![]()
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF。
∴∠BSA是二面角A—DF—B的平面角。
在RtΔASB中,![]() ∴
∴![]()
∴二面角A—DF—B的大小为60º。
(3)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,![]() ,
,
∴PQ⊥平面ABF,![]() 平面ABF,∴PQ⊥QF。
平面ABF,∴PQ⊥QF。
在RtΔPQF中,∠FPQ=60º,PF=2PQ。
∵ΔPAQ为等腰直角三角形,∴![]() 又∵ΔPAF为直角三角形,
又∵ΔPAF为直角三角形,
∴![]() , ∴
, ∴![]()
所以t=1或t=3(舍去)即点P是AC的中点。
方法二 :建立如图所示的空间直角坐标系。
(2)∵AF⊥AB,AB⊥AD,AF![]() ∴AB⊥平面ADF。
∴AB⊥平面ADF。
∴![]() 为平面DAF的法向量。
为平面DAF的法向量。
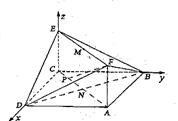 ∵
∵![]() ·
·![]() =(
=(![]() ·
·![]() =0,
=0,
∴![]() ·
·![]() =(
=(![]() ·
·![]() =0得
=0得
![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,∴
,∴![]() 为平面BDF的法向量。
为平面BDF的法向量。
∴cos<![]() ,
,![]() >=
>=![]() ∴
∴![]() 与
与![]() 的夹角是60º,即所求二面角A—DF—B的大小是60º。
的夹角是60º,即所求二面角A—DF—B的大小是60º。
(3)设P(t,t,0)(0≤t≤![]() )得
)得
![]() ∴
∴![]() =(
=(![]() ,0,0)又∵
,0,0)又∵![]() 和
和![]() 所成的角是60º。
所成的角是60º。
∴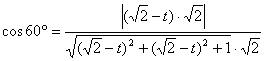 解得
解得![]() 或
或![]() (舍去),
(舍去),
19. 解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则
![]()
则![]()
即A、C两个救援中心的距离为![]()
(2)![]() ,所以P在BC线段的垂直平分线上
,所以P在BC线段的垂直平分线上
 又
又![]() ,所以P在以A、B为焦点的双曲线的左支上,且
,所以P在以A、B为焦点的双曲线的左支上,且![]()
∴双曲线方程为![]()
BC的垂直平分线的方程为![]()
联立两方程解得:![]()
![]()
∴∠PAB=120°所以P点在A点的北偏西30°处
(3)如图,设![]()
![]()
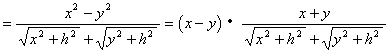
又∵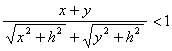
![]()
![]() 即A、B收到信号的
即A、B收到信号的
20.(1)![]() =ax2+bx-a2, ∵ x1,x2是f (x)的两个极值点,
=ax2+bx-a2, ∵ x1,x2是f (x)的两个极值点,
∴ x1,x2是方程![]() =0的两个实数根. 3分
=0的两个实数根. 3分
∵ a>0,∴ x1x2=-a<0,x1+x2=-. ∴ x1+x2= x1-x2=.
∵ x1+x2=2,∴ +4a=4,即 b2=4a2-4a3.
∵ b2≥0,∴ 0<a≤1. 7分
(2)设g(a)=4a2-4a3,则 g '(a)=8a-12a2=4a(2-3a).
由g '(a)>0Û0<a<,g '(a)<0Û<a≤1,得
g(a)在区间(0,)上是增函数,在区间(,1)上是减函数, 10分
∴ g(a)max=g()=. ∴ b≤. 14分
21. (本小题满分16分)
解(Ⅰ)令y=0,x=1得:f(1)=f(1)·f(0)![]() f(1)(1-f(0))=0,
f(1)(1-f(0))=0,
∵f(1)≠0, ∴f(0)=1
∵x>0时,f(x)>1
而由点到面①可知:1=f(0)=f(-x+x)=f (-x)·f(x)
∴f(x)=![]()
∴x<0时,0<f(x)<1
∴x∈R时,0<f(x)
设x1<x2,由f(x2)=f[x1+(x2-x1)]=f(x1)·f(x2-x1)
而x1-x2>0,∴f(x2-x1)>1
∴f(x2)=f[x1+(x2-x1)]=f(x1)·f(x2-x1)>f(x1)
∴f(x)在R上是单调递增函数.
(Ⅱ)因为数列{an}满足a1=f(0)=1,且f(an+1)=![]()
由(Ⅰ)可得f(an+1)=f(an+1)
即an+1=an+1
∴an+1-an=1(n∈N*)
∴an=n(n∈N*)
(Ⅱ)令bn=k(k∈N*)是最接近![]() 的正整数,
的正整数,
则k-![]()
由于k,n都是正整数 ∴k2-k+1≤n≤k2+k
所以满足bn=k的正整数n有k2+k-(k2-k+1)+1=2k个;
312<1000<322,322-32+1=993
T1000=![]()
=![]()
=![]() =64+
=64+![]()