全国统一标准测试数学试验(二)
（试验修订教材版）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.
第Ⅰ卷 (选择题共60分)
注意事项：
1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2
.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.
3.考试结束，监考人将本试卷和答题卡一并收回.
参考公式：
sinα+sinβ＝2sin
cos
sinα－sinβ＝2cossin
cosα+cosβ＝2coscos cosα－cosβ＝－2sinsin
一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)
1.已知M={xx=3k,k∈Z},P={xx=3k+1,k∈Z},Q={xx=3k－1,k∈Z},若a∈M ,b∈P,c∈Q,则a+b－c∈
A.M B. P C. Q D. M∪P
2.设函数f(x)=x+
,则过点（2，
）处的切线的斜率是
A. 
B.
C.
D.
3.设一组数据的方差是S2，将这组数据的每个数据都乘以5，所得到的一组新数据的方差是
A. 
S2
B. 
S2 C.5S2
D.25S2
4.函数f(x)=x－1+x－2+x－3最小值是
A.0 B.1 C.2 D.3
5.已知等差数列前n项和为Sn，若S15<0,S14>0,则此数列中绝对值最小的项为
A.第6项 B.第7项 C.第8项 D.第9项
6.若一个圆的圆心在抛物线y2=4x的焦点处，且此圆与直线x+y+1=0相切，则这个圆的方程是
A.x2+y2－2x－1=0 B.x2+y2+2x+1=0
C.x2+y2－2y+1=0 D.x2+y2+2y+1=0
7.设两个独立事件A和B都不发生的概率为
，A发生B不发生的概率与B发生但A不发生的概率相同，则事件A发生的概率P（A）等于
A. 
B.
C.
D.
8.已知线段AD∥平面α，且与平面α的距离等于3，点B是平面α内的动点，且满足AB=5，若AD=8，则点D与点B的距离d满足
A.d的最大值为
最小值为
B.d的最大值为3
，最小值为5
C.d无最大值，最小值为5
D.d的最大值为3，无最小值
9. A={1，2，3，4，5}，B={6，7，8，9}，从集合A到集合B的映射中，满足f(1)≥f(2)≥f(3)≥f(4)≥f(5)的映射有
A.21个 B.27个 C.48个 D.56个
10.若f(x)是R上的减函数 ，且f(x)的图象经过点A（0，4）和点B（3，－2），则当不等式f(x+a)－1<3的解集为（－1，2）时，a的值为
A.0 B.－1 C.1 D.2
11.直线x－y+3=0与曲线
=1的交点个数为
A.1个 B.2个 C.3个 D.4个
12.计算机将信息转换成二进制进行处理，二进制即“逢2进1”，如（1101）2表示二进数，将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数
转换成十进制形式是
A.217－2 B.218－2 C.218－1 D.217－1
第Ⅱ卷 (非选择题 共90分)
注意事项：
1.第Ⅱ卷，用钢笔或圆珠笔直接答在试题卷中.
2.答卷前将密封线内的项目填写清楚.
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题(本大题共4小题，每小题4分，共16分请将答案直接填在题中的横线上)
13.在平面直角坐标系中，若方程m(x2+y2+2y+1)=(x－2y+3)2表示的曲线是双曲线，则m的取值范围是__________.
14. 在(1－x)6(1+x+x2)的展开式中，x2的系数为__________.
15. 将函数y=sin2x的图象按向量a=（h,k）平移（0<h<
）得函数y=2sin2x的图象，则h+k等于__________.
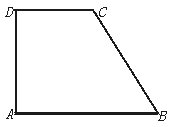16.已知四个面都是直角三角形的三棱锥，其中三个面展开后构成一直角梯形ABCD，如图，AD⊥AB，AD⊥DC，AB=2，BC=
，CD=1，则这个三棱锥外接球的表面积是__________（结果可含π）.
三、 解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤)
17.（本小题满分12分）
在△ABC中，若sinA=tanB,tan
=sinB,求证：A=C.
18.（本小题满分12分）
某厂生产A、B两种产品，需甲、乙、丙三种原料，每生产一吨产品需耗原料如下表.现有甲原料200吨，乙原料360吨，丙原料300吨，若产品生产后能全部销售，试问A、B各生产多少吨能获最大利润.
| 甲 | 乙 | 丙 | 利润（万元/吨） | |
| A产品 | 4 | 9 | 3 | 7 |
| B产品 | 5 | 4 | 10 | 12 |
19.(本小题满分12分)
已知等比数列{an}的各项均为正数，公比q≠1,数列{bn}满足b10=23,b25=－22,且(bn+1－bn+2)logma1+(bn+2－bn)logma3+(bn－bn+1)logma5=0,(n∈N*).
(1)求数列{bn}的通项公式
（2）设cn=bn,求数列{cn}前n项的和Sn.
20.(本小题满分12分）
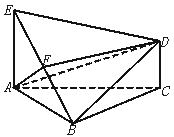
如图，△ABC中，AC=BC，AE和CD都垂直于平面ABC，且AE=AB=2，F为BE的中点，DF∥平面ABC，
（1）求CD的长；
（2）求证：AF⊥BD；
（3）求平面ADF与平面ABC所形成的较小的二面角的度数.
21.(本小题满分12分)
已知函数f(x)=
(3x－b)的图象过点A（1，2），（2，5）
（1）求函数f－1(x)的解析式；
（2）记an=3f-1 (n),n∈N*,是否存在正数k,使得（1+
）(1+
)…(1+
)≥k
对一切n∈N*均成立，若存在求出k的最大值，若不存在说明理由.
22.（本小题满分14分）
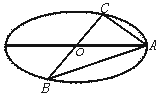已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个顶点，BC过椭圆中心O，如图，且
·
=0，BC=2AC，
（1）求椭圆的方程；
（2）如果椭圆上两点P、Q使∠PCQ的平分线垂直AO，则总存在实数λ,使
=λ
,请给出证明.