甘肃兰州02-03年高三数学模拟(一)

说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120　分钟.

参考公式：

sinα+sinβ=2sincos

sinα-sinβ=2cossin

cosα+cosβ=2coscos

cosα-cosβ=-2sinsin

正棱台、圆台的侧面积公式

S_台侧= (c′+c)l

其中c′、c分别表示上、下底面周长，l表示斜高或母线

台体的体积公式

V_台= (S′++S)h

其中S′、S分别表示上、下底面面积，h表示高.

第Ⅰ卷(选择题　共60分)

一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)

1.设集合M={x｜x=,m∈Z},N={x｜x=,m∈Z},则M、N之间的关系是

A.M=N　　　　　　　 B.MN　　　　　　  C.MN　　　　　　 D.M∩N=

2.已知f(x+1)=x²+x+1，那么f(x)的最小值是

A.0　　　　　 　　　 B.1　　　　　　　　　C.-　　　　  　　 D.

3.(理)过点(1,2)且与原点距离最大的直线方程为

A.x+2y-5=0　　　　　　　　　　　　 　　　　 B.2x+y-5=0

C.x-2y+5=0　　　　　　 　　　　　　　　　　 D.2x+y+5=0

(文)直线x+3y-1=0的倾斜角是

A.30°　　　　　　　 B.60°　　　　　　　 C.120°　　　　　　  D.150°

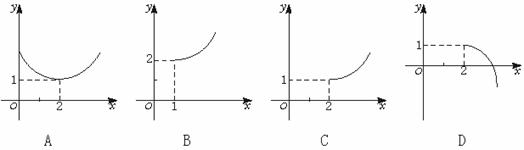
4.函数y=+2(x≥1)的反函数的图象是

　 5.已知f(x)是奇函数且在(0,+∞)上单调递增，又f(-2)=0，则不等式xf(x)＜0的解集是

A.(-2,0)∪(0,2)　　　　　　　　　　　　　　  B.(-∞,-2)∪(0,2)

C.(-∞,-2)∪(2,+∞)　　　　　　　　　　　　  D.(-2,0)∪(0,+∞)

6.已知a＞2，则=的值等于

A.0　　　　　　　　 B.　　　　　　　　  C.a　　　　　　　  D.-

7.(理)直线l: (t为参数0＜α＜＝的倾斜角为

A.α　　　　　　　  B. -α　　　　　　  C. +α　　　　　 D.α-

(文)方程x²+y²+ax+2ay+2a²+a-1=0表示圆，则a的取值范围是

A.-2＜a＜0　　　　　　　　　　　　　　　  B.-2＜a＜

C.- ＜a＜2　　　　　　　　　　　　　　  D.a＜-2或a＞

8.如图以8个点中的三个点为顶点的三角形的个数是

A.56　　　　　　　　　　　　　　　　　  B.48　　　　 

C.45　 　　　　　　　　　　　　　　　　 D.42

9.双曲线-+(y-1)²=1的两个焦点坐标是

A.(4,1)和(0,1)　　　　　　　　　　　　　　  B.(2,3)和(2，-1)

C.(3,1)和(-1,1)　　　　　　　　　　　　　　 D.(2,4)和(2,0)

10.(理)函数y=5sin(x+φ)是偶函数的充要条件是

A. =2kπ+ (k∈Z)　　　　　　　　　　  B. =kπ+ (k∈Z)

C. =2kπ(k∈Z)　　　　　　　　　　　　  D. =kπ+ (k∈Z)

(文)已知一个平面与正方体的十二条棱所成的角都等于θ，则sinθ的值等于

A.　　　　　　　  B.　　　　　　  C.　　　　　　　 D.

11.(理)已知圆锥的母线长为4，若过该圆锥顶点的所有截面面积的范围是(0,4］，则该圆锥侧面展开图扇形的圆心角是

A. 　　　　　　　　B. π　　　　　　 C.π　　　　　　  D.π或π

(文)已知圆锥的侧面积是它的底面积的两倍，则圆锥的轴截面的顶角是

A.45°　　　　　　 B.60°　　　　　　　  C.90°　　　　　　　  D.120°

12.有一张250×160的矩形钢板，欲将其切割出直径为40的小圆面，若不计切割中的损耗，则最多可以切割出小圆面的个数是

A.21　　　　　　　 B.23　　　　　　　　  C.25　　　　　　　　 D.27

第Ⅱ卷(非选择题　共90分)

二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)

13.若在(x²-)ⁿ的展开式中，x的一次项是第6项，则n=________.

14.不等式＞x+1的解集是________.

15.(理)过抛物线y²=4x的焦点的一条直线交抛物线于A、B两点，若线段AB的中点的横坐标为3，则｜AB｜=________.

(文)若抛物线y²=4(x-m)以y轴为准线，则m=________.

16.(理)设a、b表示直线，α、β、γ表示平面，给出下列命题：

①若α⊥γ，且β⊥γ，则α∥β.

②若α内有不共线的三个点到β的距离相等，则α∥β.

③若aα,bβ,且a∥β,a∥b,则α∥β.

④若a、b是异面直线，aα,bβ，且a∥β,b∥α，则α∥β.

其中正确命题的序号是________.(把正确的序号都填上)

(文)已知直线a、b和平面α，给出下列命题：

①若a⊥α，且bα，则a⊥B.

②若a∥b，且a⊥α，则b⊥α.

③若a⊥b，且b⊥α，则a∥α ,或aα.

④若a∥α，且bα，则a∥B.

其中正确命题的序号是________.(把正确的序号都填上)

三、解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分12分)

已知 tg(+α)=-，求的值.

18.(本小题满分12分)

设复数z₁=+i，复数z₂满足｜z₂｜=2，已知z₁z₂²是纯虚数，且argz₂∈(,),　　　 求z₂.

19.(本小题满分12分)

在三棱锥P—ABC中，∠PAB=∠PAC=60°，PA与底面ABC所成的角为45°，AB=AC，

(1)求证：PA⊥BC；

(2)若PA、AB、BC的长成等差数列，求侧面PBC与底面ABC所成二面角的大小.

20.(本小题满分12分)

某县地处沙漠边缘，当地居民与风沙进行着艰苦的斗争，到2002年底全县的绿地已占全县面积的30%，从2003年起县政府决定加大植树造林，开辟绿地的力度，每年将有16%的原沙漠地带变成绿地，但同时原绿地的4%又被风沙侵蚀，变成了沙漠.

(1)设全县面积为1，记2002年底的绿地面积为a₁，经过n年后的绿地面积为a_n+1，试用a_n表示a_n+1；

(2)在这种政策指导下，全县绿地面积能超过80%吗？

21.(本小题满分12分)

(理)设f(x)是定义域为(-∞,0)∪(0,+∞)的奇函数，且在(-∞,0)上是增函数.

(1)若f(1)=0，解关于x的不等式f［log_a(1-x²)+1］＞0，其中a＞1;

(2)若mn＜0，m+n≤0，求证：f(m)+f(n)≤0.

(文)已知函数f(x)=2(log₂x)²+2alog₂+b，当x=时f(x)有最小值-8.

(1)求实数a、b的值；

(2)求不等式f(x)＞0的解集.

22.(本小题满分14分)

(理)设椭圆的方程为=1，射线y=x(x≥0)与椭圆的交点为A，过A作倾斜角互补的两条直线AB、AC，与椭圆交于异于A的点B和C.

(1)求证：直线BC的斜率为定值；

(2)求△ABC面积的最大值.

(文)椭圆的方程为+y²=1，F是它的左焦点，

(1)设M是椭圆上一动点，求△OFM的重心的轨迹方程；

(2)过F作直线l与椭圆交于P、Q两点，且与椭圆的左、右准线分别交于A、B两点，当｜FA｜、｜PQ｜、｜FB｜成等比数列时，求直线l的方程.