北京西城02-03年高三数学(文)模拟(二)

学校___________班级___________姓名___________

参考公式：

三角函数的和差公积公式

圆台的体积公式

其中r′、r分别表示上、下底面半径，h表示圆台的高。

一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合要求的。每小题选出答案后，用铅笔在下表中将对应答案标号涂黑。

答案：（1）ABCD（2）ABCD（3）ABCD（4）ABCD（5）ABCD（6）ABCD（7）ABCD

（8）ABCD（9）ABCD（10）ABCD

（1）函数，则f(x)的值域是（）

（A）（2，+∞）（B）（3，+∞）

（C）（4，+∞）（D）

（2）双曲线的两个焦点坐标分别是（）

（A），（B），

（C）（-1，0），（1，0）（D）（0，-1），（0，1）

（3）函数 最小正周期是（）

（A）1（B）2

（C）π（D）2π

（4）如果复数（其中i为虚数单位，b为实数）的实部和虚部互为相反数，那么b等于（）

（A）（B）

（C）（D）2

（5）α，β是两个不重合的平面，在下列条件中，可判定平面α与β平行的是（）

（A）m，n是α内两条直线，且m∥β，n∥β

（B）α，β都垂直于平面γ

（C）α内不共线三点到β的距离都相等

（D）m，n是两条异面直线，m在α内，n在β内，且m∥β，n∥α

（6）如果0<a<1，那么下列不等式中正确的是（）

（A）（B）

（C）（D）

（7）在等比数列中，，，则（）

（A）（B）

（C）（D）

（8）某人制定了一项旅游计划，从7个旅游城市中选择5个进行游览。如果A、B为必选城市，并且在游览过程中必须按先A后B的次序经过A、B两城市（A、B两城市可以不相邻），则有不同的游览线路（）

（A）120种（B）240种

（C）480种（D）600种

（9）设偶函数在（0，+∞）上单调递减，则f（b-2）与f（a+1）的大小关系是（）

（A）f（b-2）=f（a+1）（B）f（b-2）>f（a+1）

（C）f（b-2）<f（a+1）（D）不能确定

（10）设函数f(x)的定义域为D，如果对于任意的，存在唯一的，使（C为常数）成立，则称函数y=f(x)在D上的均值为C。给出下列四个函数：

①；②y=4sinx；

③y=lgx；④

则满足在其定义域上均值为2的所有函数是（）

（A）①②（B）③④

（C）①③④（D）①③

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

（11）_____________。

（12）若过两点的直线与圆相切，则a=_____________。

（13）一个圆台的高是上下底面半径的等比中项，这个圆台高为1，母线长为，则这个圆台的体积为_____________。

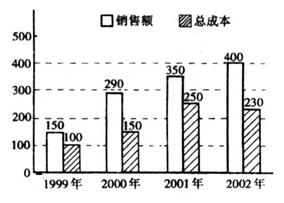
（14）如图是某企业几年来关于生产销售的一张统计图表，关于该企业近几年的销售情况，有以下几种说法：

①这几年该企业的利润逐年提高；

（注：利润=销售额-总成本）；

②1999年至2000年是该企业销售额增长最快的一年；

③2000年至2001年是该企业销售额增长最慢的一年；

④2001年至2002年该企业销额增长最慢，但由于总成本有所下降，因而2002年该企业的利润比上一年仍有所增长。

其中说法正确的是_____________（注：把你认为是正确说法的序号都填上）。

三、解答题：本大题共6小题，共84分。解答应写出文字说明，证明过程或演算步骤。

（15）（本小题满分12分）

已知，，，求tg（α-2β）的值。

（16）（本小题满分12分）

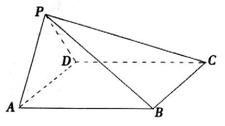
四棱锥P-ABCD中，底面ABCD是菱形，并且∠DAB=60°，侧面PAD为正三角形，其所在平面垂直于底面ABCD。

（I）求证：AD⊥PB；

（Ⅱ）求二面角A-BC-P的大小。

（17）（本小题满分14分）

已知函数（k为常数），A（-2k，2）是函数图象上的点。

（I）求实数k的值及函数的解析式；

（Ⅱ）将的图象沿x轴向右平移3个单位，得到函数y=g（x）的图象。求函数 最小值。

（18）（本小题满分14分）

某家用电器的生产厂家根据其产品在市场上的销售情况，决定对原来以每件2000元出售的一种产品进行调价，并按新单价的八折优惠销售，结果每件产品仍可获得实际销售价20%的利润。已知该产品每件的成本是原销售单价的60%。

（I）求调整后这种产品的新单价是每件多少元？让利后的实际销售价是每件多少元？

（Ⅱ）为使今年按新单价让利销售后的利润总额不低于20万元，今年至少应销售这种产品多少件？

（每件产品利润=每件产品的实际售价-每件产品的成本价）

（19）（本小题满分16分）

已知椭圆 ：的一条准线方程是，其左、右顶点分别是A、B；双曲线的一条渐近线方程为3x-5y=0。

（I）求椭圆的方程及双曲线的离心率；

（Ⅱ）在第一象限内取双曲线上一点P，连结AP交椭圆于点M，连结PB并延长交椭圆于点N，若点M恰为线段AP的中点，求证：MN⊥AB。

（20）（本小题满分16分）

已知数列是由正数组成的等差数列，是其前n项的和，并且，。

（I）求数列的通项公式；

（Ⅱ）证明：不等式对一切n∈N均成立；

（Ⅲ）若数列的通项公式满足，是其前n项的和，试问整数是否是数列中的项？若是，则求出相应的项数；若不是，请说明理由。