北京市东城区2002年高三总复习练习一
数学(理工农医类)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。第I卷1至2页。第II卷3至8页。共150分。考试时间120分钟。
第I卷 (选择题共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的和差化积公式
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
正棱台、圆台的侧面积公式
![]()
其中c′、c分别表示上、下底面周长,l表示斜高或母线长
台体的体积公式
![]()
其中S′、S分别表示上、下底面积,h表示高
第I卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.数轴上三点A、B、C的坐标分别为2、3、5,则点C分有向线段![]() 所成的比为
所成的比为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知函数y=f(x)的反函数为![]() ,则f(1)等于
,则f(1)等于
A.0 B.1 C.-1 D.4
3.若数列![]() 的前n项和公式为
的前n项和公式为![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设![]() ,则S等于
,则S等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数y=arccos(x-1)图象的对称中心的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.两圆ρ=sinθ与ρ=1的位置关系是
A.相交 B.内切 C.外切 D.内含
7.已知圆台的轴截面是上、下底边长分别为2和4,底角为60°的等腰梯形,则圆台侧面展开图的面积为
A.24π B.8π C.6π D.3π
8.已知图①中的图象对应的函数为y=f(x),则图②中的图象对应的函数
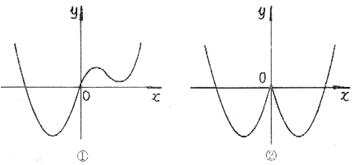
在下列给出的四式中,只可能是
A.y=f(x) B.y=f(x) C.y=f(-x) D.y=-f(x)
9.已知正四棱台![]() 的上下底面边长分别为2和4,侧棱长为2,则它的一条侧棱
的上下底面边长分别为2和4,侧棱长为2,则它的一条侧棱![]() 与截面
与截面![]() 所成角的正弦值为
所成角的正弦值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知![]() ,
,![]() ,则α+β是
,则α+β是
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
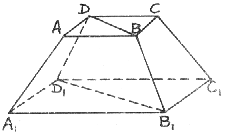
11.如图,已知多面体ABC-DEFG中,AB、AC、AD两两互相垂直,平面ABC//平面DEFG,平面BEF//平面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为
A.2 B.4
C.6 D.8
12.椭圆![]() (a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为c,则椭圆的离心率为
(a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为c,则椭圆的离心率为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第II卷(非选择题共90分)
注意事项:
1.第II卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.设复数![]() ,则
,则![]() 在复平面内对应的点位于第__________象限。
在复平面内对应的点位于第__________象限。
14.将抛物线![]() 绕其焦点按逆时针方向旋转90°后,所得抛物线的方程为____________________。
绕其焦点按逆时针方向旋转90°后,所得抛物线的方程为____________________。
15.空间内五个点中的任意三点都不共线,由这五个点为顶点只构造出了四个三棱锥,则这五个点最多可以确定__________个平面。
16.已知集合A、B、C,A={直线},B={平面},C=A∪B,若a∈A,b∈B,c∈C,在下列命题中
①![]() ②
②![]() ③
③![]() ④
④![]()
正确命题的序号是__________________。(注:把你认为正确的序号都填上)。
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
已知△ABC中,三内角A、B、C的对边分别为a、b、c,若A、B、C成等比数列,且公比式![]() ,
,
求证:![]() 。
。
18.(本小题满分12分)
已知函数![]() ,将y=f(x)的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数y=g(x)的图象。
,将y=f(x)的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数y=g(x)的图象。
(I)求y=g(x)的解析式及定义域;
(II)求函数F(x)=f(x)-g(x)的最大值。
19.(本小题满分12分)
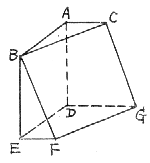
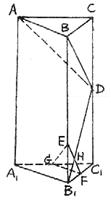
在直三棱柱![]() 中,∠ABC=90°,BC=2,
中,∠ABC=90°,BC=2,![]() 。D、F、G分别为
。D、F、G分别为![]() 的中点,EF与
的中点,EF与![]() 相交于H。
相交于H。
(I)求证:![]() ;
;
(II)求证:平面EGF//平面ABD;
(III)求平面EGF与平面ABD的距离。
20.(本小题满分12分)
已知数列![]() 中,
中,![]() 且对任意自然数n都有
且对任意自然数n都有![]() 。数列
。数列![]() 对任意自然数n都有
对任意自然数n都有![]() 。
。
(I)求证数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(III)设数列![]() 前n项的和为
前n项的和为![]() ,求
,求![]() 的值。
的值。
21.(本小题满分12分)
运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择,它们的速度分别为v千米/小时,2v千米/小时,10v千米/小时。每千米的运费分别为a元、b元、c元,且b<a<c。又这批海鲜在运输过程中的损耗为m元/小时。若使用三种运输工具分别运输时各自的总费用(运费与损耗之和)互不相等。试确定使用哪种运输工具总费用最省。(题中字母均为正的已知量)
22.(本小题满分14分)
椭圆![]() (a>b>0)与直线x+y-1=0相交于A、B两点,且OA⊥OB(O为坐标原点)。
(a>b>0)与直线x+y-1=0相交于A、B两点,且OA⊥OB(O为坐标原点)。
(I)求证:满足上述条件的各椭圆过定点![]() ;
;
(II)若椭圆的长轴长的取值范围是![]() ,求椭圆离心率的取值范围。
,求椭圆离心率的取值范围。
参考答案:
一、
1.B 2.C 3.B 4.A 5.A 6.B 7.C 8.C 9.B 10.B 11.B 12.D
二、
13.四
14.![]()
15.7
16.②
三、
17.证明:由已知,![]() ,解得
,解得![]()
则![]() ,
,![]() ………………………………………………………………………3分
………………………………………………………………………3分
![]() ……………………………………………………5分
……………………………………………………5分
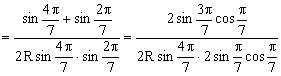 …………………………………………9分
…………………………………………9分
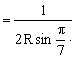 ………………………………………………………………………………11分
………………………………………………………………………………11分
![]() …………………………………………………………………………………………12分
…………………………………………………………………………………………12分
18.解:(I)由已知,将函数![]() 进行坐标变换
进行坐标变换
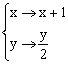
得![]() ,
,![]()
![]() 。 (x>-2) ………………………………………………4分
。 (x>-2) ………………………………………………4分
(II)![]() (x>-1)
(x>-1)
![]()
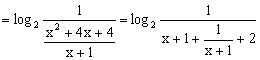 …………………………………………6分
…………………………………………6分
∵x+1>0
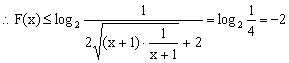 ……………………………………10分
……………………………………10分
当且仅当![]() ,即x=0时取等号。
,即x=0时取等号。
![]() 。 …………………………………………………………………12分
。 …………………………………………………………………12分
19.(I)证:由直三棱柱的性质,得平面ABC⊥平面![]() ,又由已知,AB⊥BC,
,又由已知,AB⊥BC,
∴AB⊥平面![]() 。
。
又![]() ,
,![]() ……………………………………………………2分
……………………………………………………2分
由已知,![]()
在Rt△BCD与![]() 中可求得
中可求得![]()
则![]() ,即
,即![]() 。
。
又AB∩BD=B,![]() 。 ……………………………………………………4分
。 ……………………………………………………4分
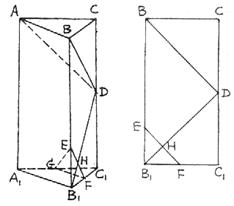
(II)证:由![]() ,在
,在![]() 中,求得
中,求得![]() 。
。
∴EF//BD …………………………………………………………………………………5分
而![]() ,
,![]() ,
,
∴EF∥平面ABD。 ……………………………………………………………………6分
∵G、F分别为![]() 的中点,
的中点,
∴![]() ………………………………………………7分
………………………………………………7分
而![]() ,
,![]() ,
,
∴GF//平面ABD………………………………………………8分
∵![]() ,
,![]() ,
,
∴平面EGF//平面ABD ……………………………………………………9分
(III)解:∵![]() ,平面EGF//平面ABD。
,平面EGF//平面ABD。
![]() 。
。
则HD为平行平面EGF与平面ABD之间的距离 ……………………………………10分
![]() ………………………………………………12分
………………………………………………12分
20.(I)证明:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,(n=1,2,3,……)
,(n=1,2,3,……)
∴![]() 是公比为
是公比为![]() 的等比数列 …………………………………………………………5分
的等比数列 …………………………………………………………5分
(II)![]() 。
。
![]() 。
。
由![]() 得
得![]() 。
。
解得![]() ………………………………………………………………9分
………………………………………………………………9分
(III)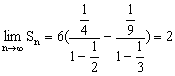 …………………………………………………12分
…………………………………………………12分
21.解:设运输路程为S(千米),使用汽车、火车、飞机三种运输工具分别运输时各自的总费用分别为![]() (元),
(元),![]() (元),
(元),![]() (元)。
(元)。
则由题意得![]()
![]()
![]() ……………………………………………………………………………3分
……………………………………………………………………………3分
![]()
∵a>b,且各字母均为正值,
![]() ,即
,即![]() …………………………………………………………………6分
…………………………………………………………………6分
那么![]() 中的最小值只可能是
中的最小值只可能是![]() 。
。
![]() 。
。
令![]() ,由c>b及各字母均为正值,
,由c>b及各字母均为正值,
解得![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
答:当![]() 时,用火车运输总费用最省 …………………………………………9分
时,用火车运输总费用最省 …………………………………………9分
当![]() 时,用飞机运输总费用最省 ………………………………………9分
时,用飞机运输总费用最省 ………………………………………9分
22.(I)证明:由方程组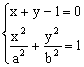 ,消去y,并整理得
,消去y,并整理得
![]()
由直线与椭圆有两个交点,得
![]()
![]()
解得![]()
设A、B两点的坐标分别为![]() 、
、![]()
则![]() ,
,![]() ① ……………………………………2分
① ……………………………………2分
由OA⊥OB得![]() ② …………………………………………………3分
② …………………………………………………3分
由A、B在直线x+y-1=0上,得
![]() ③
③
![]() ④…………………………………………………………………………4分
④…………………………………………………………………………4分
将③④代入②消去![]() ,然后再将①代入,并化简得
,然后再将①代入,并化简得
![]()
![]() ……………………………………………………………………6分
……………………………………………………………………6分
![]() ,
,
即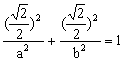
则椭圆过定点(![]() ) ……………………………………………………8分
) ……………………………………………………8分
(II)解:![]() ,则
,则![]() ,即
,即![]() 。
。
![]() 。
。
由(I)得![]() 。
。
将![]() 代入消去
代入消去![]() ,得
,得
![]()
整理后得![]() …………………………………………11分
…………………………………………11分
由已知:![]() ,得
,得![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ……………………………………………………………………14分
……………………………………………………………………14分