绝密 ★ 启用前（十一月号）

03-04年高三数学(文)全国统一标准测试(二)

命题范围：第四章　向量；第五章　不等式

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分.共150分，考试时间120分钟.

参考公式：

sinαcosβ=［sin（α+β）+sin（α－β）］　　 

cosαsinβ=［sin（α+β）－sin（α－β）］

cosαcosβ=［cos（α+β）+cos（α－β）］　　

sinαsinβ=－［cos（α+β）－cos（α－β）］

sinα+sinβ=2sincos

sinα－sinβ=2cossin

cosα+cosβ=2coscos

cosα－cosβ=－2sinsin

第Ⅰ卷（选择题 共60分）

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案.不能答在试题卷上.

一、选择题（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.将函数y=cos2x的图象F按向量a=（－）平移到L，则L的函数解析式是

A.y=cos（2x+）+ 　　　　　　　　　　　　　　　　　B.y=cos（2x－）+

C.y=cos（2x+）+　　　　　　　　　　　　　　　　　　　　　D.y=cos（2x－）+

2.下列命题中，正确的是

A.若a=b，则a=b或a=－b

B.若a与b共线，则存在惟一实数λ，使a=λb

C.若a·b=0，则a=0或b=0

D.若a－b=a+b，则a与b共线

3.已知锐角三角形的三边分别为2、3、x，则x的取值范围是

A.1＜x＜5　　　　　　　　　　　　　　　　　　　　 B.＜x＜

C.0＜x＜　　　　　　　　　　　　　　　　　　 D.＜x＜5

4.已知a=8，b=15，a+b=17，则a与b的夹角θ为

A.0　　 　　　　　　　　　　 B.　　　　　　　　　　 C. 　　　　　　　　　 D.

5.若不等式x²－2ax+a＞0对x∈R恒成立，则关于t的不等式的解为

A.1＜t＜2　　　　　　　　　　　　　　　　　　　　 B.－2＜t＜1

C.－2＜t＜2　　　　　　　　　　　　　　　　　　　D.－3＜t＜2

6.在①②③④中，能得出a与b一定共线的是

①a=1－2e，b=3e　②a=e₁－e₂，b=－e₁+ e ₂ ③a=2e₁－e₂，b=e₁－e₂

④a=e₁+ e ₂，b=e₁－e ₂

A.①②　　 　　　　 B.②③　　　　　　　　　C.①③　　 　　　　　　　　D.①④

7.下列各组命题中，命题M是命题N成立的充要条件的一组命题是

A.M：a＞b；N:ac²＞bc²

B.M:a＞b，c＞d；N:a－d＞b－c

C.M:a＞b＞0，c＞d＞0；N:ac＞bc

D.M:a－b=a+b；N:ab≤0

8.在区间［－4，－1］上，函数f（x）=－x²+px+q与函数g（x）=x+同时取相同最大值，那么函数f（x）在区间［－4，－1］上的最小值为

A.－10　　 　　　　 B.－5　　　　　　　　　　C.－8　　 　　　　　　　　　D.－32

9.若，则△ABC是

A.正三角形

B.有一内角为30°的直角三角形

C.等腰直角三角形

D.有一内角为30°的等腰三角形

10.把长为12厘米的细铁丝截成两段，各自围成一个正三角形，那么，这两个正三角形面积之和的最小值是

A. cm²B.4 cm²

C.3 cm² D.2 cm²

11.已知函数y=f（x）是偶函数，y=g（x）是奇函数，它们的定义域为［－π，π］，且它们在x∈［0，π］上的图象如下图所示，则不等式＞0的解集为

A.（－，0）∪（，π）

B.（－π，－）∪（，π）

C.（－，0）∪（，π）

D.（－π，－）∪（0，）

12.某大学的信息中心A与大学各部门、各院系B，C，D，E，F，G，H，I之间拟建立信息联网工程，实际测算的费用如图所示（单位：万元），请观察图形，可以不建部分网线，而使得信息中心A与大学各部门、各院系连通（直接或中转），则最少的建网费用是

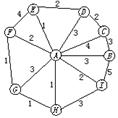
A.12万元　　　　　　　　　　　　　　　　　　　　　　　　 B.13万元

C.14万元　　　　　　　　　　　　　　　　　　　　　　　　 D.16万元

第Ⅱ卷 （非选择题 共90分）

二、填空题（本大题共4小题；每小题4分，共16分.把答案填在题中的横线上）

13.已知a∥b，a=（2，3），b=（－4，m），又c=5，c与a的夹角为60°，则（a+b）·c的值为______.

14.已知M为△ABC边AB上一点，且△AMC的面积是△ABC面积的，则B分所成的比为______.

15.已知θ是三角形的一个内角，且函数y=cosθ·x²－4sinθ·x+6对任意x∈R恒为正值，则θ的取值范围是______.

16.给出下列命题中

①（）+（）+；

②平行四边形ABCD中，有；

③矩形ABCD中，点集M={A，B，C，D}，则集合T={P，Q∈M，且P，Q不重合}中元素个数为8；

④“两个向量方向相反”是这两个向量共线的充分不必要条件.

其中正确命题的序号是______.（注：把你认为正确的命题的序号都填上）

三、解答题(本大题共6小题;共74分.解答过程应写出文字说明、证明过程或演算步骤)

17.（本小题满分12分）

已知a=3，b=2，a与b的夹角为120°，当k为何值时，

（1）ka－b与a－kb垂直；

（2）ka－2b取得最小值？并求出这个最小值.

18.（本小题满分12分）

在△ABC中，a²+b²=c²+ab，且sinAsinB=，试判定△ABC的形状.

19.（本小题满分12分）

在△ABC中，三边a，b，c为连续正整数，最大角是钝角.

（1）求最大角；

（2）求以它的最大角为内角，夹此角的两边和为4的平行四边形的最大面积.

20.（本小题满分12分）

森林失火，火势以每分钟100 m²的速度迅速蔓延，消防队接到报警后立即派消防队员前去，在失火5分钟后赶到现场开始灭火.已知每位消防队员每分钟可灭火50 m²，所消耗的灭火材料等费用每人每分钟125元，另加每次灭火所消耗的车辆、器材和装备等费用平均每人100元，而每烧毁1 m²的森林直接损失费用为60 元，设消防队派x名消防队员前去救火，从到现场直至把火完全扑灭共用n分钟.

（1）写出x与n的关系式；

（2）问x为何值时，才能使总损失最小？

21.（本小题满分12分）

a是任意的实数，解关于x的不等式（a+3）x²+2ax+a－3＞0.

22.（本小题满分14分）

已知不等式x+3＞2x①，≥1②，2x²+mx－m²＜0③.

（1）若同时满足不等式①、②的x值也满足不等式③，求m的取值范围；

（2）若满足不等式③的x值至少满足不等式①、②中的一个，求m的取值范围.

03-04年高三数学(文)全国统一标准测试(二)答案

一、1.A　2.D  3.B　4.D　5.A  6.B　7.D　8.C  9.C　10.D　11.D　12.B

二、13.－　14.－　15.0＜θ＜　16.①④

三、17.解：（1）∵ka－b与a－kb垂直，

∴（ka－b）·（a－kb）=0.　　　　　　　　　　　　　　　　　　　　　　　　　 2分

∴ka²－k²a·b－b·a+kb²=0.

∴9k－（k²+1）×3×2·cos120°+4k=0.

∴3k²+13k+3=0.

∴k=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　5分

∴当k=时，ka－b与a－kb垂直.　　　　　　　　　　 6分

（2）∵ka－2b²=k²a²－4ka·b+4b²

=9k²－4k×3×2·cos120°+4×4

=9k²+12k+16=（3k+2）²+12. 　　　　　　　　　　　　　　　　　　　　　　　10分

∴当k=－时，ka－2b取得最小值为2. 　　　　　　　　　　　　　　12分

18.解：由余弦定理，得c²=a²+b²－2abcosC.

∵a²+b²=c²+ab，

∴ab－2abcosC=0.

∴cosC=，

∴C=60°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

∵sinAsinB=，cos（A+B）=cos（180°－C）=cos120°=－，

cos（A+B）=cosAcosB－sinAsinB，

∴cosAcosB=.　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　8分

∴cos（A－B）=cosAcosB+sinAsinB=1.

∵－π＜A－B＜π，∴A－B=0.

∴A=B=60°.

∴△ABC是等边三角形.　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

19.解：（1）设a=n－1，b=n，c=n+1（n∈N^*且n≥2）　　　　 2分

因C是钝角，

所以cosC=，　　　　　　　　　　　　　 4分

所以1＜n＜4，∴n=2或3

当n=2时，a=1，b=2，c=3，不能构成三角形；

当n=3时，a=2，b=3，c=4，cosC=－，

∴C=π－arccos.即C=arccos（－）.　　　　　　　　　　　　　　　　　 8分

（2）设夹角C的两边为x，y，则x+y=4

平行四边形的面积S=xysinC=x（4－x），∴当x=2时，S_max=.　　 12分

20.解：（1）由题意知5×100+100n=50nx　　　　　　　　　　　　　　　3分

（2）设总损失费用为y元，则

y=125nx+100x+60（n+5）×100　　　　　　　　　　　　　　　　　　　　　　7分

由（1）知n=，代入上式并整理得：

y=31450++100（x－2）≥31450+2=36450（元）　　　　 10分

上式等号成立时，当且仅当=100（x－2）时.

所以当x=27时，才能使总损失最小.　　　　12分

21.解：当a+3＜0即a＜－3时，3－a＞a+3，∴＜－1， 3分

由此得不等式的解集为{x＜x＜－1，x∈R}；　　 5分

当a+3=0，即a=－3时，不等式解集为{xx＜－1，x∈R}；　7分

当a+3＞0时，由－（－1）=＞0知＞－1，　 10分

所以a＞－3时原不等式解集为{xx＜－1或x＞，x∈R}.　 12分

22.解：（1）不等式x+3＞2x①的解集为A={x－1＜x＜3，x∈R}；不等式≥1②的解集为B={x0≤x＜1或2＜x≤4，x∈R}则A∩B={x0≤x＜1或2＜x＜3}.　4分

设不等式③的解集为C，由题意知A∩BC

当m＞0时，得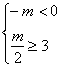，∴m≥6；

当m=0时，C是空集，不合题意；

当m＜0时，，∴m≤－3.

由此得m≤－3或m≥6.　　　8分

（2）由（1）知A∪B={x－1＜x≤4}；

由题意知CA∪B　　　10分

当m＞0时，得，∴m＞8；

当m=0时，C是空集，不合题意；

当m＜0时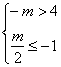，，∴m＜－4.

由此得m＜－4或m＞8.　　　14分