高三数学(文)全国统一标准测试(三)

2014-5-11 0:20:38 下载本试卷

绝密 ★ 启用前　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(十二月号)

03-04年高三数学(文)全国统一标准测试(三)

命题范围：第七章　直线与圆的方程；第八章　圆锥曲线

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分.第Ⅰ卷1至2页，第Ⅱ卷3至8页.共150分，考试时间120分钟.

参考公式：

sinαcosβ=［sin(α+β)+sin(α－β)］

cosαsinβ=［sin(α+β)－sin(α－β)］

cosαcosβ=［cos(α+β)+cos(α－β)］

sinαsinβ=－［cos(α+β)－cos(α－β)］

sinα+sinβ=2sincos

sinα－sinβ=2cossin

cosα+cosβ=2coscos

cosα－cosβ=－2sinsin

第Ⅰ卷(选择题共60分)

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案.不能答在试题卷上.

一、选择题（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

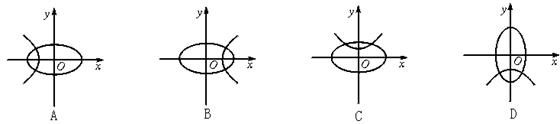
1.方程y2＝ax＋b与y2＝ax2－b表示的曲线在同一坐标系中的位置可以是

2.设直线3x+4y－5=0的倾斜角为θ,则它关于直线x=3对称的直线的倾斜角是

A.－θ　　　　　　　　　　　　　　　　　　　　　B.θ－

C.π－θ　　　　　　　　　　　　　　　　　　　　　 D.θ－π

3.若直线mx－y+m=0与抛物线y=x2－4x+3的两个交点都在第一象限，则实数m的取值范围是

A.(0,3)　　　　　　　　　　　　 　　　　　　　　　　 B.（0,3

C.(1,+∞)　　　　　　　　　　　　　　　　　　　　　 D.［1,+∞）

4.若点P为抛物线(y+2)2=4(x－1)上任意一点，以P为圆心且与y轴相切的圆必过定点M，则点M的坐标是

A. (4,－2)　　　　　　　　　　　　　　　　　　　　　B. (2,－2)

C. (1,－2)　　　　　　　　　　　　　　　　　　　　　　　　 D. (2,2)

5.已知曲线C1:y=mx－1,C2:y=1 x≤1,要使C1与C2总有交点，则m的取值范围是

A.［－1，1］　　　　　　　　　　　　　　　　　　B.（－∞，1）

C.［1，+∞　　　　　　　　　　　　　　　　　　D.（－∞，－2］∪［2，+∞)

6.已知直线l1的方程为y=x，直线l2的方程为y=ax+b(a,b为实数)，当直线l1与l2夹角的范围为［0,时，a的取值范围是

A. (,1)∪(1,)　　　　　　　　　　　　　B.(,)

C. (0，1)　　　　　　　　　　　　　　　　　　　　　 D.(1,)

7.若直线mx+2ny－4=0(m,n∈R)始终平分圆x2+y2－4x－2y－4=0的周长，则mn的取值范围是

A. (0,1)　　　　　　　　　　　　　　　　　　　　　　 B.（0，1

C.(－∞,1)　　　　　　　　　　　　　　　　　　　　 D.(－∞,1］

8.与y轴相切，且和曲线x2+y2=4(0≤x≤2)相内切的动圆圆心的轨迹方程是

A.y2=2(x+1)(0＜x≤1)

B.y2=4(x－1)(0＜x≤1)

C.y2=－4(x－1)(0＜x≤1)

D.y2=－2(x－1)(0＜x≤1)

9.若θ为三角形中最大内角，则直线l：xtanθ+y+m=0的倾斜角的范围是

A.(0,)∪(,π)　　　　　　　　　　　　　　 B.(,)∪(,)

C. (0,)∪(,　　　　　　　　　　　　D.(0,)∪(,π)

10.实数x,y满足x2+y2－6x－6y+12=0，则的最大值为

A.3　　　　　　　　　　　　　　　　　　　　　　 B.3+2

C.2+　　　　　　　　　　　　　　　　　　　　　 D.

11.过双曲线=1(a＞0,b＞0)的右焦点F，作渐近线y=x的垂线与双曲线左右两支都相交，则双曲线离心率e的取值范围为

A.1<e<2　　　　　　　　　　　　　　　　　　　　　　B.1<e<

C.e>　　　　　　　　　　　　　　　　　　　　　　D.e>2

12.1998年12月12日，太原卫星发射中心为美国摩托罗拉公司发射了两颗“铱星”系统通信卫星，卫星运行的轨道是以地球中心为一个焦点的椭圆.设其近地点距地面m千米，远地点距地面n千米，地球半径为R千米，则通信卫星运行轨道的短轴长为

A.mn千米　　　　　　　　　　　　　　　　　　　　 B. 2mn千米

C.千米　　　　　　　　　D. 2千米

第Ⅱ卷 (非选择题共90分)

二、填空题（本大题共4小题；每小题4分，共16分.把答案填在题中的横线上）

13.抛物线y2=4x的焦点为F，过点P(,1)的直线l交抛物线于A、B点，且P恰为AB中点，则｜AF｜+｜BF｜=______.

14.若点P（1，1）和Q(2，2)到直线l：2(a2－2a)x+2(b2+4b)y+15=0的距离相等，且分别在l的两侧，则a+b=______.

15.过双曲线一焦点且垂直于双曲线实轴的直线交双曲线于A、B两点.若以AB为直径的圆恰过双曲线的一个顶点，则双曲线离心率是______.

16.一个酒杯的轴截面是抛物线的一部分，它的方程是x2=2y(0≤y≤20).在杯内放入一个玻璃球，要使球触及酒杯底部，则玻璃球半径的取值范围为______. 

三、解答题(本大题共6小题；共74分.解答过程应写出文字说明、证明过程或演算步骤)

17.（本小题满分12分） 

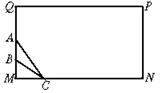
如图所示，某化工厂反应塔MQ上有温度计AB.已知｜AM｜=a,｜BM｜=b.在矩形QMNP的边MN上建观察点C较安全，观察温度计AB时视角越大越清晰.问C在线段MN上何处时，对温度计AB观察得最清晰？

18.（本小题满分12分）

已知椭圆的中心在原点，准线为x=±4，如果直线x－y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.

（1）求椭圆的方程;

（2）求过左焦点F1且与直线x－y=0平行的弦AB的长.

19.（本小题满分12分）

已知双曲线C:－y=1和点P(2,m),过点P引直线l和双曲线交于P­1、P2两点,若P恰为P１P２的中点,求m的取值范围.

20.（本小题满分12分）

有三块合金，第一块含60%的铝和40%的铬，第二块含10%的铬和90%的钛，第三块含20%的铝、50%的铬和30%的钛，现需要由它们组合成含钛45%的新合金，试求在新的合金中，含铬的百分比范围.

21.(本小题满分12分) 

已知曲线C满足：曲线C任意一点到定点A（1，0）与定直线x=4的距离和等于5.

(1)求曲线C的方程；

(2)试判断曲线C上有几对不同的点关于定点P（3，0）对称，并求出这几对点的坐标.

22.（本小题满分14分）

在△ABC中，A点的坐标为（0，3），BC边的长为2，且BC在x轴上滑动.

(1)求△ABC的外心P的轨迹方程；

(2)设一直线l：y=x+b与P的轨迹交于E、F点，原点O到直线l的距离为d，求的最大值，并求此时b的值.

03-04年高三数学(文)全国统一标准测试(三)答案

一、1.A　2.C  3.A　4.B　5.D  6.B　7.D　8.C  9.C　10.B　11.C　12.D

二、13.7　14.－1　15.2　16.(0,1)

三、17.解：要使体温计AB观察得最清晰，只要视角∠ACB最大即可，以NN，NQ所在直线为x轴，y轴，以N为坐标原点建立直角坐标系.设C(x,0),∠ACB=θ,　　　　　　3分

则tanθ=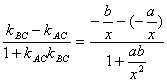=　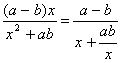　　　　　　　　　　　　　　 6分

∵a＞b,∴tanθ≤　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

等号当且仅当x=，即x=时成立.

又θ∈(0,),所以当x=时，θ取最大值arctan.

故C点应在NN上距M为处. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

18.解：(1)依题意可设椭圆方程为=1(a＞b＞0),

直线x－y=0与椭圆交点为N(c, c)(c为椭圆的半焦距)，　　　　　　　　　　　3分

则由+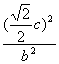=1, =4及a2－b2=c2,得a2=16,b2=8,c2=8.

所求椭圆方程为=1.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

（2）易求得直线AB的方程为y= (x+2),　　　　　　　　　　　　　　　　　　　　　 8分

代入=1,化简得x2+2x－4=0,　　　　　　　　　　　　　　　　　　　　　　　　　　　　9分

由韦达定理及弦长公式得｜AB｜=6　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

19.解：设P1(x1,y1)、P2(x2,y2)

由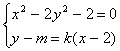去y得

(1－2k2)x2－4k(m－2k)x－2［(m－2k)2+1］=0,　　　　　　　　　　　　　　　　　　　　　　　　4分

依题意P(2,m)是P1P2的中点,

∴x1+x2=4,得km=1，①　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

又Δ＞0,

∴16k2(m－2k)2－4(1－2k2)·（－2）［(m－2k)2+1］＞0

2k2(m－2k)2－(2k2－1)［(m－2k)2+1］＞0,

(m－2k)2－(2k2－1)＞0　8分

由①式有(m－)2－(－1)＞0,

m2+－3＞0,(m2－2)(m2－1)＞0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

∴｜m｜＞或｜m｜＜1,

∴m的取值范围是(－∞,－)∪(－1,1)∪(,+∞). 　　　　　　　　　　　　　　　　　　 12分

20.解：设在一个单位重量的新合金中，含第一、第二、第三块合金重量分别为x、y、z,则含铬百分比为W=0.4x+0.1y+0.5z.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分

其中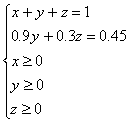消去z得

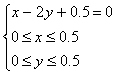即　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

（x,y）对应的点集为线段AB（包括端点）

由于W=0.4x－1.4y+0.75,即y=x+－W　①

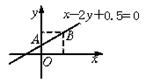
①表示的直线与线段AB有公共点，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

由此得直线截距的取值范围为≤－W≤,得0.25≤W≤0.4,

即含铬的百分比范围是［0.25,0.4］ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

21.解：（1）设C上任一点P(x,y).

当x≥4时，(x－4)+=5,

整理得y2=－16(x－5)(4≤x≤5).　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3分

当x＜4时，(4－x)+ =5,

整理得y2=4x.(0≤x＜4),

所以，y2=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

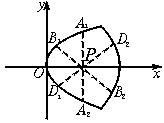
（2）因曲线C关于x轴对称，所以直线x=3与C的两个交点A1、A2关于P（3,0）对称.

由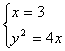知A1(3,2),A2(3,－2).　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　8分

又设B1(x1,y1),B2(x2,y2)关于P点对称，且分别在左右支上，

则由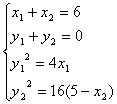　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  10分

得B1(,)、B2(,－)、D1(,－)、D2(, ).

共三对.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

22.解：（1）设B，C的坐标分别为

B(t,0),C(t－2,0),

则线段BC的中垂线方程为x=t－1,　①　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1分

AB中点（,）,AB斜率为(t≠0),

所以线段AB的中垂线方程为

y－= (x－)　②　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　3分

由①②得：x2=6y－8(－2≤x≤2且x≠－1)　③ 　　　　　　　　　　　　　　　　　　　　　　　5分

当x=－1时，t=0时，三角形外心P为(－1,),适合③；

所以P点的轨迹为x2=6y－8　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

（2）由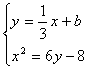得x2－2x－6b+8=0　④

x1+x2=2,x1x2=8－6b　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

所以｜EF｜==,

又因为d=,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　11分

所以=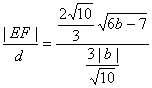

=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　13分

因方程④有两个不相同的实数根，设f(x)=x2－2x－6b+8

由题意(－2)2－4(8－6b)＞0得b＞,∴＜.　　　　　　　　　　　　　　　　　　　　　　 13分

当=时，即b=时，()max=.

所以的最大值是,此时b=. 　　　　　　　　　　　　　　　　　　　　　　　　　　　14分

03-04年高三物理全国统一标准测试(二)答案

 

1.C　2.B  3.C　4.B　5.B  6.C　7.C　8.B  9.B　10.B

11.π

12.0.24　0.4

13.

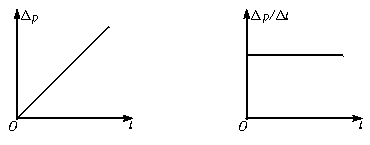
14.2∶1 

15.1000　

16.＞  11∶2

17.解析：（1）当汽车以最大速度20 m/s运动时，所受阻力与牵引力相等.

所以f=F′==80×103/20 N=4×103 N

设汽车加速运动时的牵引力为F，则由牛顿第一定律得：

F-f=ma

所以F=f+ma=4×103+2×103×2=8×103 (N)

3 s末汽车的速度为v=at=2×3=6 (m/s)

所以3 s末汽车的瞬时功率为P′=Fv=8×103×6=48 (kW)

（2）汽车匀加速运动的最大速度为　

vmax=P/F=8×104/8×103=10 (m/s)

所以汽车匀加速运动的时间为t=vmax/a=10/2=5 (s)

（3）匀加速直线运动的位移为s=at2/2=2×52/2=25 (m)

所以匀加速直线运动中汽车牵引力做的功为

W=Fs=8×103×25=2×105 (J)

18.解：v黑=＞c

所以R=2GM/c2=2.93 km

v宇宙=（2GM/R宇宙）1/2＞c

R宇宙=3c2/8ρπG=4.23×1010光年

19.解析：爆竹爆炸时爆竹和木块动量守恒.取向上为正方向，由动量守恒定律得：

mv+(-MV)=0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

(式中v、V分别是爆炸后爆竹和木块速度）

木块陷于沙中，做匀减速运动，由动能定理得：

0-MV2=-（F-Mg）s　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

爆炸后爆竹以v做竖直上抛运动，设达到的高度为h，则：

0-v2=-2gh　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　③

由②得V=0.4 m/s　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　④

④代入①得v=20 m/s　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　⑤

⑤代入③得h=20 m

20.解析：摆球从开始摆动，经摆线碰到钉子，直到线松弛，摆球做圆周运动；之后做斜抛运动击中钉子.其运动路线如图所示.

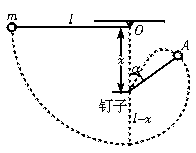
设摆球运动到和钉子的连线与竖直方向的夹角为α的A点时速度为v,并开始做抛体运动而击中钉子.

摆球自静止始做圆周运动直到A点的过程中机械能守恒：

mgl=mg(l-x)(1+cosα)+mv2/2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　①

摆球运动到和钉子的连线与竖直方向的夹角为α的A点时，由向心力公式得：

mgcosα=mv2/(l-x)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

摆球从A点开始做抛体运动，经过时间t击中钉子，则：

vtcosα=(l-x)sinα　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　③

vtsinα-gt2/2=-(l-x)cosα　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　④

③④消去t得：cosα=/3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

⑤代入②得：v2=g(l-x)/3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

⑤⑥代入①得：x=(2-3)l=0.464l