广西南宁02-03年上学期高三数学期中考试

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分。考试时间120分。

第Ⅰ卷（选择题　共60分）

参考公式：

三角函数的积化和差公式

sinαcosβ=[ sin（α+β）+sin（α－β）]　 cosαsinβ=[ sin（α+β）－sin（α－β）]

cosαcosβ=[cos（α+β）+cos（α－β）]　 sinαsinβ=-[ sin（α+β）+sin（α－β）]

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．  已知集合M={x│≤0}，N={x│x＜a＝。若M∩N≠φ，那么a的取值范围是（　　）

（A）（-∞，2）]　　（B）（-1，+∞）　　（C）[-1，+∞]）　　 （D）[-1，1]

2．  如果ctgθ=－，（＜θ＜π＝，则sin（θ+π）的值为（　　　　 ）

（A）-　　　　（B）-　　　 （C）　　　　（D）

3．  若=cos2θ，（θ≠，k∈Z）成立，则θ在（　　　）

（A）第一象限　　（B）第二象限　　  （C）第三象限　　　（D）第四象限

4．  不等式│-x²+5x│＜6的解集是（　　　　 ）

（A）（-1，2）∪（3，6）　　　　 （B）（-∞，-1）∪（2，3）∪（6，+∞）

（C）（-6，1）∪（2，3）　　　　 （D）（-3，-2）∪（-1，6）

5．下列函数中，既在开区间（0，π）内是增函数，又是以2π为最小正周期的偶函数是（　　 ）

（A）y=│sinx│　　　 （B）y=1-cos² （C）y=2^cosx　  （D）y=ctg

6．若a、b、c∈R，且ab+bc+ca=1，则下列不等式成立的是（　　　　）

（A）a²+b²+c²≥2　　　　　　　 （B）（a+b+c）²≥3

（C）　　　　 （D）abc（a+b+c）≤

7．函数y=sinx-cosx的图象可由函数y=sinx+cosx的图象（　　　　 ）

（A）向右平移个单位而得到　　  （B）向左平移个单位而得到

（C）向右平移个单位而得到　　  （D）向左平移个单位而得到

8．若log_a＜1，则a的取值范围是（　　　）

（A）（0，）　　（B）（，+∞）　　（C）（，1）　　（D）（0，）∪（1，+∞）

9．函数f（x）=cos²x+sinx在区间[ -，]上的最小值是（　　  ）

（A）　　  （B）-　　 （C）-1　　　（D）

10．若是f（x）偶函数，且当x∈[ 0，+∞]时，f（x）=x-1，则f（x-1）＜0的解集是（　　）

（A）{x│-1＜x＜0＝＝}　　　　  （B）{x│x＜0或1＜x＜2＝＝＝}

（C）{x│0＜x＜2＝＝}　　　 　 （D）{x│1＜x＜2＝＝}

11．函数y=log[ cos（）]的单调递减区间为（　　　　）

（A）[ 6kπ-，6kπ+]　　　（B）[-6kπ-，-6kπ-]

（C）[6kπ-，6kπ+]　　　 （D）[-6kπ+，-6kπ+]

（k∈Z）

12．已知α，β均为锐角，且sinα=sin（α+β），则α，β的大小关系是（　　　　）

（A）α＜β　　 （B）α＞β　　 （C）α≥β　　  （D）α、β的大小关系不确定

二、填空题：本大题共4分，共16分。把答案填在题中横线上。

13．求值：=　　　　　　　　　　  。

14．不等式2^3x+2-2^x+2＜2^x-2^-x的解集是　　　　　　　　　　　　　　　　  。

15．不等式≥0的解集为　　　　　　　　　　　　　　　　 。

16．已知3sinβ=sin（2α+β），α、β为锐角且α+β≠，则tgβ的最大值是　　　　 。

三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或步骤。

17．（本小题满分12分）

求函数y=（sinx+cosx）²+2cos²x的最小正周期。

18．（本小题满分12分）

解不等式：1-log₂（x+4）＜2log（x-2）

19．（本小题满分12分）

设函数f（x）=sin（ωx+φ）（ω＞0，-＜φ＜＝＝），给出以下三个论断：

①它的图象关于直线x=； ②它的最小正周期等于π；

③它在区间[ ]的最大值为。

以其中的两个论断作为条件，余下的论断作为结论，试写出你认为正确的一个命题，并证明。20。（本小题满分12分）

设A={x‖x-│≤}，B={x│x²-3（a+1）x+2（3a+1）≤0}，其中a∈R，若AB，求a的取值范围。

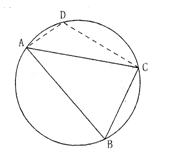21．（本小题满分，14分）在△ABC中，A、B、C的对边分别为a、b、c，已知b=2，B=60°，a+c=10。

（1）求cos；

（2）若D为△ABC外接圆劣弧一点，

且2AD=DC，求四边形ABCD的面积。

22．（本小题满分12分）

已知函数f（x）=ax²-bx+c（a＜0，b、c∈R＝，g（x）=ax+c，f（x）=0在0＜x＜1内有两相异实根。

（1）试比较g（1）与2f（0）的大小；

（2）试判断b-2c的正负符号，并证明。

南宁二中高三年级段考答题卷数学

一、选择题：（每小题5分，共60分）

1C　 2B　 3D　 4A　 5B　 6B　 7C　 8D　 9D　10C　 11A　 12A

二、填空题：本大题共4分，共16分。把答案填在题中横线上。

13．-

14．（-1，0）（没有写成集合得零分）

15．[-，0 ]）∪（0，2）]

16．

三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或步骤。

17．（本小题满分12分）

解：y=1+sin2x+2cos²x

=sin2x+cos2x+2

=sin（2x+）+2

∴前小正周期T=π

18．解：原不等式化为：1-log²（x+4）＜-2log（k-2）

即

∴

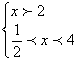
故原不等式的解集为{x│2＜x＜4}

19．（本小题满分12分）

解：①②③[ ①③②　　②③①都正确 ]

证：由②知ω=2

又①得sin（2·+y）=±1

∴y=kπ+=kπ+　 k∈△

而-　　 ∴y=

从而f（x）=sin（2x+）在区间[，]单调递减

∴有最大值f（）=　即命题成立

20．（本小题满分12分）

法一：A={x│2a≤x≤a²+1}

B={x│（x-2）[ x-（3a+1）]≤0}

（1）当2＜3a+1时有B={1≤x≤3a+1}

由A≤B得　　 解得　 1≤a≤3

（2）答2=3a+1时有AB

（3）当2＞3a+1时，解得a=-1

故a=-1或1≤a≤3

法二：A={x│2a≤x≤a²+1}

令f（k）=（x-2）[ x-（3a+1）]≤0

由A≤B得

解得：a=-1或1≤a≤3

21．（本小题满分14分）

解：（1）法一：∵由已知得

∴cosc=或

∴cos=cos（60°-c）

=cos60°cosc+sin60°sinc

=

（2）∴S_△ABC=6

S_△ACD=2

∴S_△=8

（1）法二：由正弦定理得

∴sinA+sinC=

∴cos

22．解：（1）f（0）=c　　g（1）=a+c

∴g（1）-2f（0）=a-c

设f(x)=0的两根为x₁、x₂则

x₁+x₂=　 ∈（0，2）　 2a＞b＞0　　①

x₁+x₂=　 ∈（0，1）　 a＞c　　　　②

∴g（1）＞2f（c）

（2）∵f（x）＞0有两根　故 b²-4ac≥0

由②得　b²≥4ac＞2bc

∴b＞2c

即 b-2c＞0（答对得2分）