朝阳区高三数学综合练习

2003．5

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。

第Ⅰ卷（选择题共50分）

注意事项：

1． 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：

三角函数的和差化积公式

正棱台、圆台的侧面积公式

其中c′、c分别表示上、下底面周长，l表示斜高或母线长

台体的体积公式

其中S′、S分别表示上、下底面面积，h表示高

一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）集合M={（x，y）x+yi=1，x∈R，y∈R}，集合N={（x，y）x+y=1}，则M∩N的真子集的个数为

（A）1　　（B）2　　（C）3　　（D）4

（2）x≤2的必要但不充分条件是

（A）x+1≤3　　（B）x+1≤2　　

（C）x+1≤1　　（D）x-1≤1

（3）函数y=f（x）的图象和图象关于直线对称，则f（x）解析式为

（A）　　（B）

（C）　　（D）

（4）已知函数y=f（x）的反函数，则f（1）等于

（A）0　　（B）1　　（C）-1　　（D）4

（5）若定义在区间（-1，0）内的函数满足f（x）>0 ，则a的取值范围是

（A）　　（B）　　

（C）　　（D）（0，+∞）

（6）若方程表示双曲线，则双曲线的准线方程为

（A）　　（B）

（C）　　（D）

（7）“五一”节期间，某商场为吸引顾客，实行“买100送20的连环送”活动，即顾客购物每满100元（不满100元部分忽略不计），就可以获赠商场购物券20元，并且购物可以用现金，也可以用购物券，如果你有680元现金，在活动期间到该商场购物，最多可以获赠购物券累计

（A）120元　　（B）136元　　（C）140元　　（D）160元

（8）已知α、β、γ、δ为平面，a、b为直线，P为点，则下列命题中正确的是

（A）若a、b是异面直线，且、，则过P有且只有一个平面与a、b都平行

（B）若a、b是异面直线，则存在α、β使，，且α⊥β

（C）若α∩β=a，b//a，则b//α且b //β

（D）若α∩β=a，γ∩δ=b，且α⊥γβ⊥δ则a//b

（9）已知a>b，且，那么a的取值范围是

（A）a<-1　　（B）-1<a<0　 

（C）a>1　 （D）a>1或-1<a<0

（10）设f（x）=xsinx，若、，且，则下列不等式恒成立的是

（A）　　（B）　　

（C）　　（D）

第Ⅱ卷（非选择题共100分）

注意事项：

1．第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试卷中。

2．答卷前将密封线内的项目填写清楚。

二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。

（11）f（x）为偶函数，当x∈[0，+∞）时，f（x）=x-1，那么f（x-1）<0的解集为____。

（12）已知直线x+2y-3=0和圆交于两点M、N，O为坐标原点，且OM⊥ON，则F=________。

（13）f（x）=（3a-1）x+b-a，x∈（0，1]，若f（x）≤1恒成立，则a+b的最大值为____。

（14）点P是棱长为2的正四面体木块ABCD的棱AB的中点，从点P开始要锯出与棱AB垂直的截面，当锯到某个位置时因故停止，这时量得在面ABD上的锯痕PM=1，在面ABC上的锯痕，则锯缝MN=________。

三、解答题：本大题共6小题，共84分。解答应写出文字说明，证明过程或演算步骤。

（15）（本小题满分14分）

在△ABC中，a、b、c分别是角A、B、C的对边，若。

（Ⅰ）求解A；

（Ⅱ）若，b+c=3，求b与c的值。

（16）（本小题满分14分）

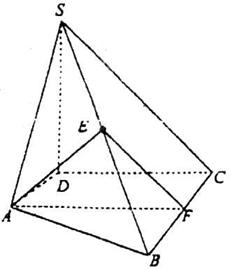
如图，四棱锥S-ABCD的底面ABCD是直角梯形，已知SD⊥底面ABCD，

且∠ADC=∠BCD=90°，BC=CD=2AD。

（Ⅰ）求证：平面SBC⊥平面SCD；

（Ⅱ）E为侧棱SB上的一点，为何值时，AE//平面SCD，证明你的结论；

（Ⅲ）若SA=AB，求二面角C-SB-D的大小。

（17）（本小题满分14分）

函数　　　 f（x）对一切实数x、y均有f（x+y）-f（y）=（x+2y+1）x成立，且f（1）=0

（Ⅰ）求f（0）的值；

（Ⅱ）求f（x）的解析式；

（Ⅲ）解不等式

（18）（本小题满分14分）

某乡镇为改善投资环境准备对全乡镇公路建设进行投资，本年度投入为800万元，以后每年投入将比上年减少；据测算本年度将增加收入400万元，由于投资环境的逐年改善，预计今后每年增加收入会比上年增加。

（Ⅰ）求出n年内（本年度为第一年）总投入万元和n年内增加总收入万元的表达式；

（Ⅱ）问经过多少年，增加的总收入超过总投入。

（19）（本小题满分14分）

动点P到定点F（-1，0）的距离与到定直线x=4的距离的一半的和为4。

（Ⅰ）求P点的轨迹C的方程；

（Ⅱ）若动直线l与C相交于M、N，且M、N与坐标原点O连线的斜率的乘积为定值，求证为定值。

（20）（本小题满分14分）

函数f（x）满足f（x+y）+1=f（x）+f（y），f（0.5）=0，且x>0.5时；f（x）<0。

（Ⅰ）设，求数列的通项公式；

（Ⅱ）证明当时，；

（Ⅲ）判断f（x）的单调性，并证明。

高三数学综合练习参考答案及评分标准

2003．5

一、选择题

1．C　2．A　3．B  4．C　5．A　6．A　7．D　8．B　9．D　10．D

二、填空题

11．（0，2）

12．3

13．

14．1

三、解答题

15．（Ⅰ）解：由及得

……2分

……4分

……6分

又A为△ABC的内角　∴A=60°……8分

（Ⅱ）解：由余弦定理得，又……10分

∴（1）

又b+c=3　　　　 （2）……12分

由（1）（2）得，或。……14分

16．（Ⅰ）证明：∵SD⊥底面ABCD，∴SD⊥BC

又BC⊥CD，故BC⊥平面SCD……2分

，故平面SBC⊥平面SCD……4分

（Ⅱ）时，AE//平面SCD

证明：取SB的中点为E，BC的中点为F，连接AF……6分

则AF//CD，EF//SC

故EF//平面SCD，AF//平面SCD；平面AEF//平面SCD。……8分

而，∴AE//平面SCD……10分

（Ⅲ）解：设AD=a，则BC=CD=2a。

于是，故。

作CO⊥BD于O，

又SD⊥平面BCD，故SD⊥CO，故CO⊥平面SBD。

连接SO，△SBO是△SBC在平面SBD上的射影。……12分

设二面角C-SB-D的平面角为θ

则，故θ=60°。……14分

17．（Ⅰ）解：f（1）-f（0）=（1+1）×1=2，∴f（0）=2……3分

（Ⅱ）解：f（x）-f（0）=x（x+1），∴……6分

（Ⅲ）解：

∵

∴当△<0，即-4<a<4时，解集为R……8分

当△≥0，即a≥4或a≤-4时，

方程的两根为

，

……10分

故（1）当a=±4时，不等式的解集为……12分

（2）当a>4或a<-4时，不等式的解集为

……14分

18．（Ⅰ）解：第1年投入800万元，

第2年为万元，

……

第n年为万元。……2分

∴

……4分

第1年增收400万元，

第2年增收为万元，

……

第n年为万元。……6分

∴

……8分

（Ⅱ）解：由题意，即。

解得，（舍去）……12分

又n∈N，得n≥5，

答：经过5年增加的总收入超过总投入。……14分

19．解：（Ⅰ）设P（x，y），

则，

……2分

∵当x≥4时，，不合题意。

∴……4分

∴化简得……6分

（Ⅱ）设，，

由（Ⅰ）得，……8分

故（1）

（2）

（3）

（1）×（2）得（4）……10分

由（3）得

由（3）（4）得，同理……12分

∴……14分

20．（Ⅰ）解：f（1）=f（0.5+0.5）=f（0.5）+f（0.5）-1=-1……1分

令x=n，y=1，f（n+1）=f（n）+f（1）-1=f（n）-2

∴，……3分

∴数列是等差数列，，公差

∴。……4分

（Ⅱ）证明：用数学归纳法。

（1）n=1时，，则，∴f（2x）≤0

又f（2x）+1=2f（x），∴。

故n=1时，命题成立。……6分

（2）假设n=k时命题成立

即时，

n=k+1时，，

则……8分

故n=k+1时，命题成立。

综上所述，n∈N时命题成立。……10分

（Ⅲ）解：在R上是减函数

设，且，则。

当时，。

∴　　……12分

当时，由（Ⅱ）知当时

∵n→∞时，，∴时，f（x）<1。

∴，∴

∴当时，

故f（x）是减函数。……14分