高三第二学期期中练习
数 学(理科)
2002.5![]()
学校________________ 班级_______________姓名_________________
| 题号 | 一 | 二 | 三 | 总分 | |||||
| (17) | (18) | (19) | (20) | (21) | (22) | ||||
| 分数 | |||||||||
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面积公式
![]()
![]() ,
,
其中![]() 、
、![]() 分别表示上、下底面周长,
分别表示上、下底面周长,![]() 表
表
![]() 示斜高或母线长
示斜高或母线长
![]() 台体的体积公式
台体的体积公式
![]()
![]()
其中S/、S分别表示上、下底面积,h表示高
一.选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 函数y =![]() 的定义域是
( )
的定义域是
( )
(A) (1,![]() (B) (1, 2)
(C) (2, +
(B) (1, 2)
(C) (2, +![]() ) (D) (-
) (D) (-![]() ,2)
,2)
(2) 极坐标系内,点(2, ![]() )关于直线
)关于直线 ![]() 的对称点坐标为
( )
的对称点坐标为
( )
(A) (![]() ) (B) (2,
) (B) (2, ![]() ) (C) (0, 0) (D) (2, 0)
) (C) (0, 0) (D) (2, 0)
(3) 直角梯形ABCD中,AB//DC, AB = 2CD, ![]() A = 45
A = 45![]() , AD = 2. 以直线AB为轴将梯形ABCD旋转一周所得旋转体的体积为 ( )
, AD = 2. 以直线AB为轴将梯形ABCD旋转一周所得旋转体的体积为 ( )

(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
(4) 已知复数![]() ,复数
,复数![]() ,那么
,那么![]() 的三角形式为 ( )
的三角形式为 ( )
(A) 2![]() (B)
2
(B)
2![]()
(C) 2![]() (D)
2
(D)
2![]()
(5) 函数y = cosx (-![]() < x < 0) 的反函数为
( )
< x < 0) 的反函数为
( )
(A) y = arccosx (-1 < x < 1) (B) y = - arccosx (-1 < x < 1)
(C) y = -![]() + arccosx (-1 < x < 1)
(D) y =
+ arccosx (-1 < x < 1)
(D) y =![]() - arccosx (-1 < x < 1)
- arccosx (-1 < x < 1)
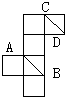
(6) 将正方体的纸盒展开(如图),直线AB, CD在原正方体中的位置关系是 ( )
(A) 平行 (B)垂直 (C) 相交且成60![]() 角 (D) 异面且成60
角 (D) 异面且成60![]() 角
角
(7)从7人中选出5人到10个不同交通岗的5个中参加交通协管工作,则不同的选派方法有( )
(A)![]() 种 (B)
种 (B)![]() 种 (C)
种 (C)
![]() 种 (D)
种 (D)![]() 种
种
(8) 已知a, b是直线,![]() 是平面,给出下列命题:①
是平面,给出下列命题:①![]() ,则
,则![]() ;②
;②![]() ,则
,则![]() ;③
;③![]() ,则
,则![]() ;④
;④![]() ,则
,则![]() . 其中正确命题的序号是 ( )
. 其中正确命题的序号是 ( )
(A) ①②④ (B) ①③④ (C) ②④ (D) ②③
(9)等比数列{an}公比为q, 则“a1 > 0, 且q > 1”是“对于任意自然数n, 都有an+1 > an”的 ( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分又非必要条件
(10)已知f (x)是奇函数,定义域为{x x![]() R, x
R, x![]() 0}. 又f (x)在区间(0, +
0}. 又f (x)在区间(0, +![]() )上是增函数,且f (-1) = 0, 则满足f (x) > 0的x的取值范围是
( )
)上是增函数,且f (-1) = 0, 则满足f (x) > 0的x的取值范围是
( )
(A) (1, +![]() ) (B) (0, 1) (C) (-1, 0)
) (B) (0, 1) (C) (-1, 0)![]() (1, +
(1, +![]() ) (D) (-
) (D) (-![]() , -1)
, -1)![]() (1, +
(1, +![]() )
)
(11)若不论k为何值,直线y = k(x – 2) + b与曲线x2 – y2 = 1总有公共点,则b的取值范围是 ( )
(A) ![]() (B) [
(B) [![]() (C) (-2, 2) (D) [-2, 2]
(C) (-2, 2) (D) [-2, 2]
(12)在一次足球预选赛中,某小组共有5个球队进行双循环赛(每两队之间赛两场),已知胜一场得3分,平一场得1分,负一场得0分.积分多的前两名可出线(积分相等则要比净胜球数或进球总数).赛完后一个队的积分可出现的不同情况种数为 ( )
(A) 22 (B) 23 (C) 24 (D) 25
二. 填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上.
(13) 若 (x +![]() )
)![]() 的展开式中第三项系数为36,则自然数n的值是_________.
的展开式中第三项系数为36,则自然数n的值是_________.
(14) 若集合{(x, y)
x + y – 2 = 0且x – 2y + 4 = 0}![]() {(x, y) y = 3x
+ b}, 则b = _________ .
{(x, y) y = 3x
+ b}, 则b = _________ .
(15) 现有两个定值电阻,串联后等效电阻值为R,并联后等效电阻值为r.若R=k r,则实数k 的
取值范围是 ________________.
(16) 已知函数f (x) = x2 –2ax + b (x![]() R).给出下列命题:①f(x)必是偶函数;②当f(0) = f(2)时f(x)的图象必关于直线x = 1对称;③若a2–b <
0,则f(x)在区间[a, +
R).给出下列命题:①f(x)必是偶函数;②当f(0) = f(2)时f(x)的图象必关于直线x = 1对称;③若a2–b <
0,则f(x)在区间[a, +![]() )上是增函数;④f(x)有最大值a2–b.
其中正确命题的序号是___________________
.
)上是增函数;④f(x)有最大值a2–b.
其中正确命题的序号是___________________
.
三.解答题:本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤.
(17) (本小题满分12分)
已知![]() .
.
(I)化简![]() 的解析式;
的解析式;
(II)若![]() ,求
,求![]() 使函数
使函数![]() 为偶函数;
为偶函数;
(III)若![]() 为偶函数, 求满足
为偶函数, 求满足![]() =1,
=1,![]() 的
的![]() 的集合.
的集合.
(18) (本小题满分12分)
解关于![]() 的不等式:
的不等式:![]() (
(![]() )
)
(19) (本小题满分12分)
如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成角的正切值为![]() .
.
(I)求侧面PAD与底面ABCD所成二面角的大小 ;
(II) 若E是PB中点,求异面直线PD与AE所成角的正切值;
(III) 在侧面PAD上寻找一点F, 使EF⊥侧面PBC.试确定F点的位置,
并加以证明.

(20) (本小题满分12分)
矩形ABCD的顶点A、B在直线![]() 上,C、D在抛物线
上,C、D在抛物线![]() 上,该矩形的外接圆方程为
上,该矩形的外接圆方程为![]() .
.
(I)求矩形ABCD对角线交点M的坐标;
(II)求此矩形的边长,并确定![]() 的值.
的值.
(21) (本小题满分12分)
这是一个计算机的程序的操作说明:
(1)初始值x = 1,y = 1, z = 0, n = 0;
(2) n = n + 1 (将当前n + 1的值赋予新的n);
(3) x = x + 2(将当前x + 2的值赋予新的x);
(4) y = 2y(将当前2y的值赋予新的y);
(5) z = z + xy (将当前z + xy的值赋予新的z);
(6)如果z > 7000,则执行语句(7),否则回语句(2)继续进行;
(7)打印n, z;
(8)程序终止.
由语句(7)打印出的数值为______,_______.
以下写出计算过程:
(22) (本小题满分14分)
已知函数![]() .
.
(I)将![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(II)函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称,求函数
对称,求函数![]() 的解析式.
的解析式.
(III)设![]() ,已知
,已知![]() 的最小值是m且
的最小值是m且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
高三数学期中练习(理科)参考答案
2002.5
一.选择题(每小题5分,共60 分)
(1) B (2) A (3) A (4) D (5) B (6) D (7) D (8) B (9) A (10) C (11) B (12) C
二.填空题 (每小题4分,共16分)
(13) 9
(14) 2 (15) [4, +![]() ﹚ (16) ③
﹚ (16) ③
三.解答题
(17) 本小题满分12分
解:(I) ![]() 2分
2分
=![]() 4分
4分
=![]()
(或![]() 6分
6分
(II) 当![]() 时,
时,![]() 为偶函数.
8分
为偶函数.
8分
(III) 由![]() 10分
10分
![]()
∴所求x的集合是![]()
![]() 12分
12分
(18)本小题满分12分
解:原不等式可化为![]() 1分
1分
原不等式成立的必要条件是![]()
![]()
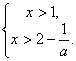 3分
3分
由 ![]() 且
且 ![]() , 故
, 故 ![]() 5分
5分
∴原不等式等价于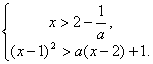
![]()
 7分
7分
若![]() 则
则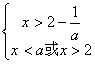
又![]() , ∴
, ∴![]() .
9分
.
9分
∴![]() .
.
若![]() , 则
, 则 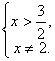 ∴
∴![]() 且
且![]() 10分
10分
若![]() >
>![]() ,则
,则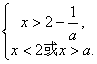 ∵ 2>2-
∵ 2>2-![]() ,
,
∴![]()
![]() .
12分
.
12分
综上,当1< ![]() 时 ,不等式的解集是
时 ,不等式的解集是![]()
![]()
![]() }
}
当 ![]() 时 , 不等式的解集是
时 , 不等式的解集是![]()
![]() 且
且![]() }
}
当 ![]() >
>![]() 时 , 不等式的解集是
时 , 不等式的解集是![]()
![]()
![]() }
}
(19) 本小题满分12分

解:(Ⅰ) 连结AC,BD交于O,连结PO.
∵P-ABCD为正四棱锥,
∴PO⊥底面ABCD.
作PM⊥AD于M,连结OM,
∴OM⊥AD.
∴ ∠PMO为侧面PAD与底面
ABCD所成二面角的平面角. 2分
∵ PO⊥底面ABCD,
∴ ∠PAO为PA与底面ABCD所成的角.
∴![]() ∠PAO=
∠PAO=![]() . 设AB=
. 设AB=![]() , ∴ AO=
, ∴ AO=![]() MO=
MO=![]() .
.
∴PO=![]()
![]()
![]() . ∴
. ∴![]() ∠PMO=
∠PMO=![]() .
.
∴ ∠PMO=![]() ,即侧面PAD与底面ABCD所成的二面角为
,即侧面PAD与底面ABCD所成的二面角为
![]() . 4分
. 4分
(Ⅱ) 连结EO,∵E为PB的中点,O为BD的中点,∴EO//PD.
∴∠AEO为异面直线AE与PD所成角 6分
∵ Rt△PAO中, AO=![]() PO=
PO=![]() ∴PA=
∴PA=![]() .
.
∴EO=![]() PD=
PD=![]() .由AO⊥截面PDB,可知AO⊥EO.
.由AO⊥截面PDB,可知AO⊥EO.
在Rt△AOE中 ![]() ∠AEO=
∠AEO=![]() .
.
即异面直线AE与PD所成角的正切值是![]() .
8分
.
8分
(Ⅲ) 延长MO交BC于N,连结PN,取PN中点G,连结EG,MG.
∵P-ABCD为正四棱锥且M为AD的中点, ∴N为BC中点. ∴BC⊥MN,BC⊥PN.
∴BC⊥平面PMN. ∴平面PMN⊥平面PBC.
∵PM=PN, ∠PMN=![]() ,∴△PMN为正三角形, ∴MG⊥PN, ∴MG⊥平面PBC.
,∴△PMN为正三角形, ∴MG⊥PN, ∴MG⊥平面PBC.
取AM中点为F,连结FE, 则由EG//MF且EG=MF得到MFEG为平行四边形,
∴FE//MG. ∴FE⊥平面PBC. 12分
(20) 本小题满分12分
解: (I)∵M是矩形外接圆的圆心,外接圆的方程为![]()
∴ M点坐标为(![]() .
3分
.
3分
(II) ∵CD//AB, ∴可设CD的直线方程为![]() .
.
与抛物线方程联立,消![]() ,得
,得![]() (*)
(*)
设弦CD的中点为N,则![]() .
.
由MN⊥CD,得![]() ,即
,即  ,解得
,解得![]() .
6分
.
6分
由方程(*),![]() ,
,
![]() 8分
8分
N点坐标为(![]() ,N关于M的对称点是N
,N关于M的对称点是N![]() 坐标为(-
坐标为(-![]() ,
,
N![]() 在直线AB上,代入方程可得
在直线AB上,代入方程可得![]() 10分
10分
M点到CD的距离为![]() ∴
∴![]() .
.
圆半径r满足![]() ∴
∴![]() 12分
12分
即此矩形的分别边长为![]()
(21) 本小题满分12分
解: 设n= ![]() 时,x,y,z
的值分别为
时,x,y,z
的值分别为![]() .
.
依题意,![]() ∴
∴![]() 是等差数列,
是等差数列, ![]() .
2分
.
2分
![]() ∴
∴![]() 是等比数列,
是等比数列, ![]() .
4分
.
4分
![]() 5分
5分
∴![]() =
=![]()
∴![]()
![]()
以上两式相减,得 zn=![]()
=![]() 9分
9分
依题意,程序终止时:![]() ,
,
即 可求得
可求得![]() . 12分
. 12分
(22) 本小题满分14分
解: (I) ![]() .
2分
.
2分
(II) 设![]() 图象上一点P
图象上一点P![]() ,
,
点P关于![]() 的对称点为Q
的对称点为Q![]() ,
4分
,
4分
由Q在![]() 的图象上, ∴
的图象上, ∴![]() ,
,
于是![]()
![]() , 即
, 即 ![]()
![]()
![]() .
7分
.
7分
(III) ![]() . 8分
. 8分
(1) 当![]() 时,
时, ![]() ,
, ![]()
由![]() 值域是
值域是![]() ,可得
,可得![]() 这与
这与![]() 矛盾;
矛盾;
(2) 当![]() 时,
时, ![]() ,
,![]()
![]() 是(-
是(-![]() )上的增函数,
)上的增函数,
设![]() 则当
则当![]() 时,
时, ![]() 这与已知矛盾.
这与已知矛盾.
(3) 当![]() 时,
时, ![]() ,
,![]()
![]() 是(-
是(-![]() )上的减函数,
)上的减函数,
设![]() 则当
则当![]() 时,
时, ![]() 这与已知矛盾.
11分
这与已知矛盾.
11分
由(1),(2),(3)可知, ![]() 此时
此时![]() ,
,![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,
![]() 取得最小值
取得最小值 ![]() .
.
由![]() 及
及![]() 得
得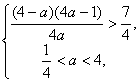
解得, ![]() .
14分
.
14分
说明:其它正确解法按相应步骤给分.