高三第二学期期末练习
数 学
2002.6
学校________________ 班级_______________姓名_________________
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面积公式
![]()
![]() ,
,
其中![]() 、
、![]() 分别表示上、下底面周长,
分别表示上、下底面周长,![]() 表
表
![]() 示斜高或母线长
示斜高或母线长
![]() 台体的体积公式
台体的体积公式
![]()
![]()
其中S/、S分别表示上、下底面积,h表示高
一.选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设全集I={1,3,5,7,9},集合![]() ={1,
={1,![]() ,则
,则![]() 的值是
( )
的值是
( )
(A) 2 (B) 8 (C) –2或8 (D) 2或8
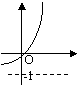
(2)函数![]() 的反函数的图象是
( )
的反函数的图象是
( )
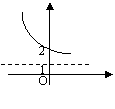
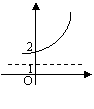

|
 y
y
y
y
y
y
y
y
x x
x x
(A) (B) (C) (D)
(3)(理)若点P ![]() 在曲线
在曲线![]() 为参数)上,则使
为参数)上,则使![]() 取得最大值的点P的坐
取得最大值的点P的坐
标是 ( )
(A) (6,-8) (B) (-6,8) (C)(3,-4) (D)(–3,4)
(文)若直线![]() 与两坐标轴交点为A、B,则以线段AB为直径的圆的方程是( )
与两坐标轴交点为A、B,则以线段AB为直径的圆的方程是( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(4) ![]() 展开式的第四项等于7,则
展开式的第四项等于7,则![]() 等于
( )
等于
( )
(A)-5
(B) ![]() (C)
(C)![]() (D)5
(D)5
(5) (理)下列命题中,使命题M是命题N成立的充要条件是 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(文)若![]() 是任意实数,且
是任意实数,且![]() ,则
( )
,则
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6) (理)已知复数![]() ,满足
,满足![]() ,那么
,那么![]() 在复平面上对应点(x,y)的轨
在复平面上对应点(x,y)的轨
迹是 ( )
(A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线
(文)复数![]() 的辐角主值是
的辐角主值是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(7) 用半径为48cm的半圆形铁皮制作上口半径为8cm,下口半径为2cm 且母线长为36cm的漏斗(不考虑接缝损耗),则最多可作
( )
(A) 1个 (B)
2个 (C) 3个 (D) 4个
(8) 某科技小组有6名同学,现从中选出3人去参观展览,至少有1名女生入选时的不同选法有16种,则小组中的女生数目为
( )
(A) 2
(B) 3
(C) 4
(D) 5
(9) (理)已知F1, F2是椭圆![]() 的两个焦点,B是短轴的一个端点,则ΔF1BF2的面积的最大值为
( )
的两个焦点,B是短轴的一个端点,则ΔF1BF2的面积的最大值为
( )
(A) ![]() (B)
(B) ![]() (C)100(3-2
(C)100(3-2![]() ) (D)
) (D)![]()
(文) 已知F1, F2是椭圆![]() 的两个焦点, B是短轴的一个端点,则ΔF1BF2的面积的最大值为
( )
的两个焦点, B是短轴的一个端点,则ΔF1BF2的面积的最大值为
( )
(A) 1
(B) 2 (C) 3 (D) 4
(10)ΔABC边上的高线为AD.BD=![]() CD=
CD=![]() 且
且![]() ,将ΔABC沿AD折成大小为
,将ΔABC沿AD折成大小为![]() 的二面角
的二面角
B-AD-C.若![]() 则棱锥A-BDC的侧面ΔABC是
( )
则棱锥A-BDC的侧面ΔABC是
( )
(A) 锐角三角形 (B) 钝角三角形 (C) 直角三角形 (D)形状与![]() 的值有关的三角形
的值有关的三角形
(11) 数列{a n}中,a 1 = 1,S n是前n项和.当n >
2时,a n = 3S n,则![]()
![]() = ( )
= ( )
(A)
-![]() (B) –2
(C) 1 (D) -
(B) –2
(C) 1 (D) -![]()
(12)对于抛物线C:![]() ,我们称满足
,我们称满足![]() 的点
的点![]() 在抛物线的内部.若点
在抛物线的内部.若点![]() 在抛物线的内部,则关于直线
在抛物线的内部,则关于直线![]()
![]() 与C
( )
与C
( )
(A)恰有一个公共点 (B)恰有两个公共点
(C)可能一个公共点也可能两个公共点 (D)没有公共点
二. 填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上.
(13) 如果![]() ,那么
,那么![]() 的值是 ____________.
的值是 ____________.
(14) 圆锥与圆柱的底面半径都是![]() 高都是
高都是![]() .已知它们的侧面积相等, 则
.已知它们的侧面积相等, 则![]() =_________.
=_________.
(15) 双曲线与椭圆![]() 有相同的焦点又过点(3,-1),则双曲线的渐近线方程是________. (16 )无穷数列{a n}同时满足条件:①对于任意自然数n,都有-2 < a n < 4;②当n为正偶数时,an-1<an且a n > a n+1;③当n > 3时,a n > 0. 请写出一个满足条件的数列{a n}的通项公式:_____________.
有相同的焦点又过点(3,-1),则双曲线的渐近线方程是________. (16 )无穷数列{a n}同时满足条件:①对于任意自然数n,都有-2 < a n < 4;②当n为正偶数时,an-1<an且a n > a n+1;③当n > 3时,a n > 0. 请写出一个满足条件的数列{a n}的通项公式:_____________.
三.解答题:本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤.
(17) (本小题满分12分)
(理科作) 解不等式:![]() .
.
(文科作) 解不等式:![]() .
.
(18) (本小题满分12分)
在ΔABC中,![]() 的对边分别为
的对边分别为![]() .若
.若![]() .
.
(I) 求![]() 的值;
的值;
(II) 设复数![]() ,求
,求![]() 的值.
的值.
(19) (本小题满分12分)
如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为![]() ,且侧面ABB1A1垂直于底面ABC.
,且侧面ABB1A1垂直于底面ABC.
(I) 证明: AB![]() CB1;
CB1;
(II) 求三棱锥B1-ABC的体积;
(III) 求二面角C-AB1-B的大小(文科求其正切值).

(20) (本小题满分12分)
某地区预计从明年初开始的前![]() 月内,对某种商品的需求总量
月内,对某种商品的需求总量![]() (万件)与月份
(万件)与月份![]() 近似关系为
近似关系为
![]() .
.
(I) 写出明年第![]() 个月的需求量
个月的需求量![]() (万件)与月份
(万件)与月份![]() 的函数关系;
的函数关系;
(II) 求出哪个月份的需求量超过1.4万件,并求出这个月的需求量.
(21) (本小题满分12分)
设二次函数![]()
![]() ,已知不论
,已知不论![]() 为何实数,恒有
为何实数,恒有![]() 和
和![]() .
.
(I) 求证:b+c=-1;
(II) 求证:![]() ;
;
(III)若函数![]() 的最大值为8,求b,c值.
的最大值为8,求b,c值.
(22) (本小题满分14分)
(文科学生只作(I) (II)小题)
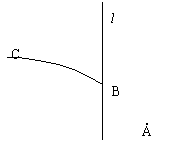
如图,BC是一条曲线段,点B在直线l上.点C到l的距离等于5,l外一点A到l的距离为2.对于曲线段BC上的任意一点P,总满足![]() ,其中d是点P到直线l的距离.
,其中d是点P到直线l的距离.
(I) 建立适当的坐标系,写出l的方程及点A的坐标,并求出点B,点C的坐标;
(II) 求出曲线段BC的方程;
(III)
设另有一定点D,![]() ,A、D位于l两侧,且点D到l的距离为a
,A、D位于l两侧,且点D到l的距离为a![]() ,求曲线段BC上的点到点D的最近距离.
,求曲线段BC上的点到点D的最近距离.
高三数学期末练习参考答案
2002.6
一. 选择题(每小题5分,共60 分)
(1) D (2) C (3) A (4) B (5) (理) D (文) B (6) D (文)A (7) C (8) A (9) B (10) C
(11) A (12) D
二. 填空题 (每小题4分,共16分)
(13) ![]() (14)
(14) ![]() (15)
(15) ![]()
(16) ![]()
![]()
![]()
三. 解答题
(17) 本小题满分12分
理 解:设![]() ,则原不等式等价于
,则原不等式等价于![]() 2分
2分
则 7分
7分
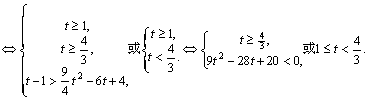
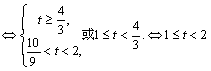 10分
10分
∴ ![]() . ∴
. ∴![]()
∴原不等式的解集是![]()
![]() }
12分
}
12分
(文)解:
设![]() , 则原不等式化为
, 则原不等式化为![]() 2分
2分
![]() 6分
6分
∴![]() .
8分
.
8分
∴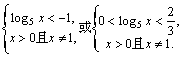 10分
10分
![]() .
12分
.
12分
∴原不等式的解集是![]()
![]() }
}
(18)本小题满分12分
解: (I)由![]() 1分
1分
∴![]() . ∴
. ∴![]() . 2分
. 2分
∵A是 △ABC的内角, ![]() .
3分
.
3分
由正弦定理知, ![]() .
.
![]() 4分
4分
由![]() .
6分
.
6分
(II) ∵![]() ,
, ![]() 8分
8分
![]() 9分
9分
故 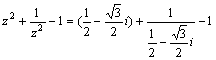 =
=![]() +
+![]() -1=0. 12分
-1=0. 12分
(19) 本小题满分12分
解:(Ⅰ) 证明: 在平面B1A内,过B1作B1D⊥AB于D. 1分
∵侧面BA1⊥平面ABC, ∴B1D⊥平面ABC. 2分
∴∠B1BA是BB![]() 与平面ABC所成的角, ∴∠B1BA=
与平面ABC所成的角, ∴∠B1BA=![]() .
3分
.
3分
∵ 三棱柱的各棱长均为2,∴ 四边形ABB1A1是菱形. △ABB![]() 为正三角形.
为正三角形.
∴ D是AB的中点,连结CD, 在正三角形ABC中, CD⊥AB.
∴ AB⊥CB1. 5分
(Ⅱ)解: ∵B1D⊥平面ABC, ∴B1D是三棱锥B1-ABC的高.
由B1B=2, ∠B1BA=![]() , ∴B1D=2sin
, ∴B1D=2sin![]() =
=![]() .
.
![]() .
8分
.
8分
(III) ∵△ABC为正三角形, CD⊥AB, CD⊥B1D, ∴CD⊥平面ABB1. 9分
在平面ABB1中作DE⊥AB1于E.连结CE,则CE⊥AB1.
∴∠CED为二面角C-AB1-B的平面角. 10分
在Rt△CED中,CD=2sin![]() =
=![]() .
.
连结BA1交AB1于O,则BO=![]() ,∴DE=
,∴DE=![]() BO=
BO=![]() .∴
.∴![]()
∴所求二面角C-AB1-B的大小为arctg2(文科: 所求二面角C-AB1-B的平面角的正切值为2)
12分
(20) 本小题满分12分
解(I): 第一个月需求量为![]() .
.
当![]() 时,第
时,第![]() 个月的需求量为
个月的需求量为![]() 5分
5分
当![]() 时,
时,![]() 也适合上式, ∴
也适合上式, ∴![]()
![]() 7分
7分
(II) 由题设可得: ![]() ,
,
解之得![]()
即第六个月需求量超过1.4万件,为1.44 万件. 12分
答: 第六个月需求量超过1.4万件,为1.44 万件.
(21) 本小题满分12分
(I) ∵![]() 恒成立, ∴
恒成立, ∴![]() .
.
∵![]() 恒成立, ∴
恒成立, ∴![]() .
.
从而知![]() . ∴
. ∴![]() . 即
. 即![]() .
4分
.
4分
(II) 由![]() ∴
∴![]()
又∵![]() . ∴
. ∴ ![]() .
8分
.
8分
(III)
∵ ![]() ,
,
当![]() 时,
时, ![]() .
.
由 ![]() 解得
解得 ![]() 12分
12分
(22) 本小题满分14分
解: (I) 以![]() 为
为![]() 轴, 且点A在
轴, 且点A在![]() 轴的正半轴上建立直角坐标系.
1分
轴的正半轴上建立直角坐标系.
1分
则![]() 的方程为
的方程为![]() , 点A的坐标为 (2,0).
2分
, 点A的坐标为 (2,0).
2分
由![]() ,可求出点B的坐标为
(0,
,可求出点B的坐标为
(0,![]() ).
3分
).
3分
设C点坐标为(![]() ,
,![]() 得
得![]()
∴![]() (舍去负值). ∴点C的坐标为 (-5,
(舍去负值). ∴点C的坐标为 (-5,![]() ). 5分
). 5分
(II) 设点P![]() 是曲线段BC上任意一点, 则
是曲线段BC上任意一点, 则![]() - (-x) = 3
- (-x) = 3
∴y2 = -2x + 5 (-5 < x < 0, y > 0) 9分
(III)
设点D (-a, 0) (a
> 0) ,点P![]() ,依题意:
,依题意:
PD =![]() =
=![]() =
=![]() 11分
11分
若-5 < 1 – a <
0, 即1 <
a < 6, 则当x = 1 – a时, PDmin
=![]() ; 12分
; 12分
若![]() , 即0 < a < 1, 则当x = 0时, PDmin
=
, 即0 < a < 1, 则当x = 0时, PDmin
=![]() ;
13分
;
13分
若![]() , 即a > 6, 则当x = -5时,PDmin
=
, 即a > 6, 则当x = -5时,PDmin
=![]() . 14分
. 14分
说明:其它正确解法按相应步骤给分.