北京市东城区2002年高三总复习练习（三）

数学

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。

第Ⅰ卷（选择题共60分）

注意事项：

1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：

三角函数的和差化积公式　　　 　　　　　　

　　　　　　 

　

　　　　　　　

　　

　　　　　　　　　　　　　　　　 

正棱台、圆台的侧面积公式

其中c '、c分别表示上、下底面周长，l表示斜高或母线长

台体的体积公式：　

其中S' 、S分别表示上、下底面积，h表示高。

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)若互不相等的三个实数a、b、c成等差数列，a、c、b成等比数列，则a:b:c等于

（A） 1：2：3　

（B）3：1：2　

（C） 4：1：2

（D）4：1：（-2）

（2）（理）已知,则x等于

（A） 　 

（B）　

（C）　

（D）

（2）（文）的值是

（A）　 （B）　

（C）　 （D）

（3）复数的共轭复数的平方等于

（A）　 （B） 　

（C） 　（D）

（4）已知异面直线a、b分别在平面α、β内，且a∩β=c,那么直线c

(A) 与a、b都相交　

（B）与a、b 都不相交

（C）只与a、b中的一条相交　

（D）至少与a、b中的一条相交

（5）（理）已知圆心的极坐标为(a,π)(a>0),则过极点的圆的极坐标方程为

（A）ρ=2αsinθ

（B）ρ=-2αsinθ

 (C)ρ=2αcosθ

(D)ρ=-2αcosθ

(5)(文)以（5，6）和（3，-4）为直径端点的圆的方程是

（A）　　

（B）

（C）　

（D）

（6）圆台母线与底面成45°角，侧面积为，则它的轴截面面积是

（A） 2　（Ｂ）3　

（C） 　 （D）

（7）在同一坐标系中，方程和（a、b均为正实数）所表示的曲线只可能是下列四个图形中的

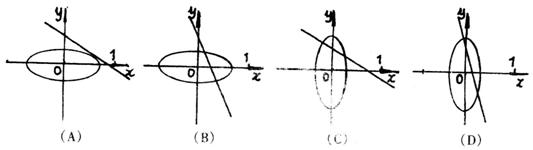
（8）把函数y=f(x)的图象沿着直线x+y=0的方向向右下方平移个单位，得到函数的图象，则

(A) 　

 (B)

(C) 　 

 (D)

(9)如图，四边形ABCD中，AD//BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A—BCD。

　　　

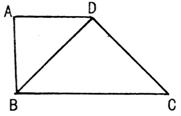
则在三棱锥A—BCD中，下列命题正确的是

（A）平面ABD⊥平面ABC

（B）平面ADC⊥平面BDC

（C）平面ABC⊥平面BDC

（D）平面ADC⊥平面ABC

（10）在平面直角坐标系中有6个点，它们的坐标分别为（0，0），（1，2），（-1，-2）（2，4）（-2，-1），（2，1）则这6个点可确定不同三角形的个数为

（A）14　 （B） 15　

（C） 16　（D） 20

（11）椭圆的焦点为和，点P在椭圆上，如果线段的中点在y轴上，那么的值为

(A) 7:1　 (B)5:1　

 (C) 9:2　 (D) 8:3

(12)已知函数y=f(x)与互为反函数，与y=g(x)的图象关于直线y=x对称.若， (x>0),则等于

(A) 1　 (B) -1　

 (C) 3　 (D) -3

第Ⅱ卷 (非选择题共90分)

注意事项:

1.第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中。

2.答卷前将密封线内的项目填写清楚。

二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。

（13）sin80°cos35°-sin10°cos55°的值等于________________.

(14) 已知抛物线的准线方程是x=-3，那么抛物线的焦点坐标是_________.

(15)已知，当时，有，则a、b的大小关系是___________________。

（16）一圆柱被一平面所截，截口是一个椭圆.已知椭圆的长轴长为5，短轴长为4，被截后几何体的最短侧面母线长为1，则该几何体的体积等于_____________。

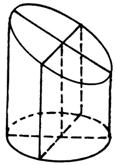
三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。

(17) （本小题满分12分）

已知：△ABC中，C=120° c=7，a+b=8 。

求：cos(A-B)的值。

(18) (本小题满分12分)

已知函数y=f(x)对任意实数，,都有，且当x>0时，

f（x）<0。

(Ⅰ)试判断函数y=f(x)的奇偶性，并给出证明；

(Ⅱ)试判断函数y=f(x)的单调性，并给出证明。

（19）.（本小题满分12分）

在边长为a的正三角形的三个角处各剪去一个四边形。这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图①。若用剩下的部分拆成一个无盖的正三棱柱形容器，如图②。则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值。

　　　

(20).（本小题满分12分）

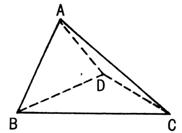
已知三棱锥p—ABC中，PC⊥底面ABC，AB=BC，D、F分别为AC、PC的中点，DE⊥AP于E.

（Ⅰ）求证：AP⊥平面BDE；

（Ⅱ）求证：平面BDE ⊥平面BDF；

（Ⅲ）若AE：EP=1：2，求截面BEF分三棱锥P—ABC所成两部分的体积比。

(21)（本小题满分12分）

已知直线l与椭圆（a>b>0）有且仅有一个交点Q，且与x轴、y轴分别交于R、S，求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程。

(22)（本小题满分14分）

已知数列的通项公式 (n∈N)，它的前n项和记为，数列是首项为3，公差为1的等差数列.

（ Ⅰ）求与的解析式；

（ Ⅱ）试比较与(n∈N)的大小。

北京市东城区2002年高三总复习练习（三）

高三数学参考答案及评分标准

一、

（1）D　（2）D　（3）B （4） D　（5）D　（6）B　（7）D　（8）A

（9）D　（10） B　（11）A　（12） D

二、

（13）　（14） （1，0）　（15）a<b　(16) 10π

三、

（17）解：由正弦定理，得

----------------------------------------2分

又由正弦定理及已知，得方程

　　 2R(sinA+sinB)=8---------------------------------------------------5分

解得-------------------------------------------------9分

∴，

　　　　　 --------------------------------------------------12分

（18）

解：(Ⅰ)在关系式中，

令，得.

解得.

同样，在已知关系式中，令, ,

得f(x-x)=f(x)+f(-x),

即f(x)+f(-x)=f(0)=0.

∴函数f(x)是R上的奇函数.-------------------------------------------------6分

(Ⅱ)任取.

则

　　　　　　 .

由，并由已知，得

即

则由函数单调性的定义，得

y=f(x)是R上的减函数.------------------------------------------------------ 12分

(19) 解：设容器的高为x.

则容器底面正三角形的边长为--------------------------------2分

∴---------------------4分

　　　

　　　

　　　

　　　-----------------------------------------------------------10分

当且仅当，即时

----------------------------------------------12分

答：当容器的高为时，容器的容积最大，最大容积为.

(20) （Ⅰ）证：∵PC⊥底面ABC，BD平面ABC，

∴PC⊥BD.

由AB=BC，D为AC的中点，得BD⊥AC.

又PC∩AC=C ，∴BD⊥平面PAC.--------------------------------------2分

又PA平面PAC，∴BD⊥PA.

由已知，DE⊥PA，DE∩BD=D,

∴AP⊥平面BDE.-------------------------------------------------------4分

（Ⅱ）证: 由BD⊥平面PAC，DE平面PAC，得BD⊥DE.

由D、F分别为AC、PC的中点，得DF∥AP.

 又由已知，DE⊥AP，∴DE⊥DF---------------------------------------6分

BD∩DF=D，∴DE⊥平面BDF.

又DE平面BDE，∴平面BDE⊥平面BDF. ----------------------8分

（Ⅲ）解: 设点E和点A到平面PBC的距离分别为和.

则--------------------------------------9分

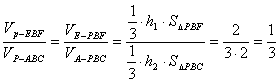∴----------------------11分

所以截面BEF分三棱锥P-ABC所成的两部分体积的比为1：2（或2：1）-----------12分

（21）解：由已知，直线l不过椭圆的四个顶点.

所以设直线l的方程为y=kx+m(k≠0).----------------------------------------------1分

代入椭圆方程，得.

化简后，得.-------------3分

　

由已知，得△=0.

即.①­--------------------------------6分

在直线方程y=kx+m中，

分别令y=0，x=0，求得 S(0，m).

令顶点P的坐标为（x，y）,

由已知，得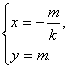　

解得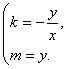　　  ­--------------------------------10分

代入①式并整理，得

即为所求.------------------------------------------12分

（22）解：（Ⅰ）由已知.

∴，∴--------------2分

，

当n≥2时，.

∴

（Ⅱ ）

当n=1时，，，有.-------------------6分

当n=2时，，，有---------------7分

当n=3时，有---------------8分

当n=4时，，有---------------9分

当n=5时，，有

猜想,当n≥4时，。证明如下：--------------------------------10分

证明

∵

∴只需证明

只需证明.

只需证明。

由平均值定理，有

∴只需证明.

只需证明.

此不等式当n≥4时成立.

所以当n≥4时成立.

综上，当n=1或n≥4，n∈N时, ；

 当n=2和n=3时，------------------14分