朝阳区高三数学第一次统一练习试卷
(理工农医类) 2002.4
(考试时间120分钟,满分150分)
成绩_____________
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题共60分)
参考公式:
三角函数积化和差公式
![]()
![]()
![]()
![]()
正棱台、圆台侧面积公式:
![]()
其中c′、c分别表示上、下底面周长,l表示斜高或母线长。
台体的体积公式:![]()
其中s′、s分别表示上、下底面积,h表示高。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡上将该选项涂黑。
(1)已知函数![]() 的定义域为M,
的定义域为M,![]() 的值域为N,则( )
的值域为N,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(2)直线![]() :ax+2y-1=0与直线
:ax+2y-1=0与直线![]() :
:![]() 平行,则a的值为( )
平行,则a的值为( )
A.-1 B.2 C.-1或2 D.0或1
(3)已知α、β是两个不同的平面,在下列条件中,可判断平面α与平面β平行的是( )
A.α、β都垂直于平面y
B.a、b是α内两条直线,且a//β,b//β
C.α内不共线的三个点到β的距离相等
D.a、b为异面直线,且a//α,b//α,a//β,b//β
(4)若以直角坐标系原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线
 (α为参数)的极坐标方程为 ( )
(α为参数)的极坐标方程为 ( )
A.![]() B.ρ=2sinθ C.ρ=sinθ
D.
B.ρ=2sinθ C.ρ=sinθ
D.![]()
(5)不等式![]() 的解集为(
)
的解集为(
)
A.{x-2≤x<2} B.{x-1<x<2}
C.{x0≤x<2} D.{xx<2}
(6)函数![]() 的最小正周期为(
)
的最小正周期为(
)
A.3π B.2π
C.π D.![]()
(7)某房地产开发商在销售一幢23层的商品楼之前接下列方法确定房价:由于首层与顶层均为复式结构,因此首层价格为![]() ,顶层由于景观好价格为
,顶层由于景观好价格为![]() ,第二层价格为
,第二层价格为![]() ,从第三层开始每层在前一层价格上加价
,从第三层开始每层在前一层价格上加价![]() ,则该商品房各层的平均价格为(
)
,则该商品房各层的平均价格为(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(8)若奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则不等式f(x-1)<0的解集为( )
A.{xx<0或1<x<2} B.{xx<-1或0<x<1}
C.{xx<-2或-1<x<0} D.{xx<0}
(9)高中一年级8个班协商级建年级篮球队,共需10名队员,若每个班至少出一名,则不同的名额分配方式有( )
A.224种 B.62种 C.36种 D.28种
(10)如图,三棱台![]() 中,上底面
中,上底面![]() 面积为
面积为![]() ,侧面
,侧面![]() 面积为2,点B到上底面
面积为2,点B到上底面![]() 及侧面
及侧面![]() 的距离均为1,则三棱台
的距离均为1,则三棱台![]() 的体积为(
)
的体积为(
)

A.![]() B.
B.![]()
C.![]() D.2
D.2
(11)已知z∈C,z=1,当arg(z-2i)取得最大值时所对应的复数z为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(12)设![]() ,
,![]() (c>0)是椭圆
(c>0)是椭圆![]() 的两个焦点,P是以
的两个焦点,P是以![]() 为直径的圆与椭圆的一个交点,且
为直径的圆与椭圆的一个交点,且![]() ,则该椭圆的离心率为(
)
,则该椭圆的离心率为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4个小题,每小题4分,共16分,把答案填在题中横线上。
(13)设数列![]() 的前n项和为
的前n项和为![]() ,则
,则![]() _____________.
_____________.
(14)已知圆台的体积为28π,高为3,上、下底面半径之比为1:2,则圆台的侧面积为_____________。
(15)抛物线型拱桥顶距离水面2米,水面宽4米,当水下降1米后,水面宽_____________米。
(16)若对n个复数![]() 存在n个不全为零的实数
存在n个不全为零的实数![]() 使得
使得![]() 成立,则称
成立,则称![]() 为“线性相关”,依此规定,能使
为“线性相关”,依此规定,能使![]() “线性相关”的实数
“线性相关”的实数![]() 依次可以取_____________。(写出一组数值即可,不必考虑所有情况)
依次可以取_____________。(写出一组数值即可,不必考虑所有情况)
三、解答题:本大题共6个小题,共74分,解答应写出文字说明,证明过程式演算步骤。
(17)(本小题满分12分)
△ABC中,角A、B、C的对边分别为a、b、c,且a、b、c成等差数列。
(Ⅰ)求证:![]() ;
;
(Ⅱ)求![]() 的值。
的值。
(18)(本小题满分12分)
解关于x的不等式:![]()
(19)(本小题满分12分)
已知直三棱柱![]() 中,直线
中,直线![]() 与面ABC成45°的角,
与面ABC成45°的角,![]()
∠ABC=90°,E、F分别为AB、![]() 的中点。
的中点。
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]()
(Ⅲ)求三棱锥![]() 的体积。
的体积。

(20)(本小题满分12分)
在西部,待开发的某地B所需要的汽油要由地处A地的炼油厂从公路运输,已知A、B两地的运输距离为S千米,汽车从A地运汽油到B地往返一次的油耗恰好等于其满载汽油的千克数W,故无法将汽油直接运到B地,为解决问题,决定在途中选定C地建设临时中转油库,先由往返于A、C之间的汽车将油运至C地,再由往返于C、B之间的汽车将油运至B地。
(Ⅰ)问汽车每千米耗油多少千克?
(Ⅱ)设A、C两地的返输距离为x千米,问一辆汽车往返于A、C之间一次可为中转油库运去多少千克油?
(Ⅲ)在(Ⅱ)条件下,问中转油库设在A、B之间何处时,运油率P最大、最大值是多少?[运油率P=(B地收到的油)÷(A地运出的油)]
(21)(本小题满分13分)
已知动双曲线的右顶点在抛物线![]() 上,实轴长恒为4,又以y轴为右准线。
上,实轴长恒为4,又以y轴为右准线。
(Ⅰ)求动双曲线的中心的轨迹方程;
(Ⅱ)求离心率取最小值时的双曲线方程。
(22)(本小题满分13分)
已知函数![]() ,g(x)=4(x-1),数列
,g(x)=4(x-1),数列![]() 满足
满足![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)求证:![]() ;
;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若![]() ,求
,求![]() 的最大项和最小项。
的最大项和最小项。
参考答案:
一、选择题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | B | D | C | A | C | B | A | C | B | C | A |
二、填空题:
(13)(理)![]() ,(文)2n;
,(文)2n;
(14)![]() ;
;
(15)![]() ;
;
(16)-4,2,1等等。
三、解答题:
(17)(Ⅰ):∵a+c=2b, …………………………(理)2分
∴sinA+sinC=2sinB=2sin(A+C),………………(理)4分(文)3分
∴![]() 。…………(文、理)6分
。…………(文、理)6分
∵![]() ,∴
,∴![]() ………………(文、理)8分
………………(文、理)8分
(Ⅱ)解:由(Ⅰ)得![]() ,
,
![]() ,…………(文、理)10分
,…………(文、理)10分
∴![]() ,∴
,∴![]() 。……………………(文、理)12分
。……………………(文、理)12分
(18)解:(理)原不等式![]() ……………………2分
……………………2分
![]() ……………………4分
……………………4分
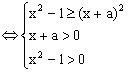 ………………6分
………………6分
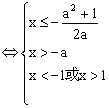 (※)………………9分
(※)………………9分
∵-a<-1,
又![]() ,
,![]() ,
,
∴![]()
∴(※)![]() ,
,
∴解集为![]() 。…………12分
。…………12分
(文)原不等式![]() ,……………………2分
,……………………2分
![]() (※),……………………………4分
(※),……………………………4分
a>1时:(※)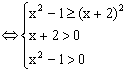

![]() ………………7分
………………7分
0<a<1时:(※)

![]() 或x>1………………10分
或x>1………………10分
综上,a>1时,解集为![]() ;0<a<1时,解集为
;0<a<1时,解集为![]() 。
。
………………12分
(19)(理)(Ⅰ)证:∵![]() 为直三棱柱,∴
为直三棱柱,∴![]() 底面ABC。
底面ABC。
∵![]() 面ABC,∴
面ABC,∴![]() 。……………………2分
。……………………2分
又AB⊥BC,BC⊥面![]() 。
。
又![]() 面
面![]() ,∴
,∴![]() 。……………4分
。……………4分
(Ⅱ)证:∵![]() 面ABC,
面ABC,
∴![]() 为
为![]() 与面ABC所成的角。
与面ABC所成的角。
∴![]() ………………………………5分
………………………………5分
∵![]() ,∠ABC=90°,
,∠ABC=90°,
∴![]() ,
,![]()
∵![]() 面ABC,且
面ABC,且![]() 面
面![]() ,
,
∴面ABC⊥面![]() 。
。
过E作EH⊥AC,垂足为H,
∴EH⊥面![]() ,过H作
,过H作![]() ,垂足为G,连EG,
,垂足为G,连EG,
∴![]() ,
,
∴∠EGH是二面角![]() 的平面角。………………8分
的平面角。………………8分
∵△AEH∽△ABC,
可求得![]() ,
,![]() ,
,
∴![]() 。
。
即二面角![]() 的正切值为
的正切值为![]() 。………………9分
。………………9分
(Ⅲ)∵![]() ,…………………………11分
,…………………………11分
由(Ⅱ)知EH⊥面![]() ,
,
∴![]() 。………12分
。………12分
(文)(Ⅰ)同理科(Ⅰ)。
(Ⅱ)证:∵![]() 面ABC,
面ABC,
∴![]() 为
为![]() 与面ABC所成的角。
与面ABC所成的角。
∴![]() ……………………5分
……………………5分
∴![]() ,
,
又![]() 面ABC,过B作BH⊥EC,垂足为H,连
面ABC,过B作BH⊥EC,垂足为H,连![]() ,
,
∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角。………………7分
的平面角。………………7分
∵△EBH∽△EBC,可求得![]() ,
,
∴![]() …………9分
…………9分
(Ⅲ)∵![]() ……………………11分
……………………11分
![]() ……………………12分
……………………12分
(20)(理)解:(Ⅰ)∵AB=S千米,每车载油量为w千克,
∴汽车每千米油耗为![]() 千克。………………4分
千克。………………4分
(Ⅱ)∵AC=x,∴CB=S-x,
∴自A地往返C地一次,汽车油耗为![]() 千克。……………………6分
千克。……………………6分
∴一辆汽车自A地到C地余下的油量为![]() 千克………………8分
千克………………8分
(Ⅲ)由(Ⅱ)结论可知,为使中转油库得到一车油,必须从A地运出![]() 千克油,从中转油库满载一车油到B地,B地可收到的油为
千克油,从中转油库满载一车油到B地,B地可收到的油为![]() 千克………10分
千克………10分
∴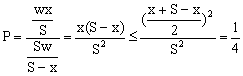 ……………………(文)12分
……………………(文)12分
当且仅当x=S-x,即![]() 地
地![]() 。
。
∴当油库设在两地运输道路的中点时运油率P最大,最大值为![]() ……………(理)12分(文)13分
……………(理)12分(文)13分
(文)(Ⅰ)(Ⅱ)见理科(22)题(Ⅰ)(Ⅱ)
(Ⅲ)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ………………12分
………………12分
(21)解:(理)(Ⅰ)设双曲线的中心为(x,y),依题意x<0,
∵a=2,∴双曲线右顶点为(x+2,y)……………………2分
依条件点(x+2,y)在![]() 上,∴
上,∴![]() ………………4分
………………4分
∴双曲线中心的轨迹方程为![]() ………………5分
………………5分
(Ⅱ)∵a=2,∴c最小题,e最小。
设双曲线方程为![]() ,……………………6分
,……………………6分
![]() 且准线方程为x=0,
且准线方程为x=0,
∴![]() ………………7分
………………7分
∴![]() 。
。
由(Ⅰ)知![]() ,
,
∴![]() ,
,
……………… 10分
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 当且仅当b=12时取等号,
当且仅当b=12时取等号,
此时![]() ,
,![]() ,
,
所求双曲线方程为![]() ………………13分
………………13分
(文)见理科20题
(22)(理)(Ⅰ)∵![]() ………………1分
………………1分
又![]() ,
,![]()
∴![]() ,
,
∵![]() ,∴
,∴![]() ………………3分
………………3分
(Ⅱ)∵![]() ,
,![]() ,
,![]() ,
,
猜测![]() 为等比数列。………………(文科20题)6分
为等比数列。………………(文科20题)6分
证明: ,
,
∴![]() 是首项为1、公比为
是首项为1、公比为![]() 的等比数列,
的等比数列,
∴![]() 。………………(理)6分(文科20题)9分
。………………(理)6分(文科20题)9分
(Ⅲ)由(Ⅱ)知,
![]() ,
,
![]() ……………………7分
……………………7分
![]() ,……………………10分
,……………………10分
设![]() ,函数
,函数![]() ,当x≥0时,
,当x≥0时,![]() ,
,
∵![]() 为减函数,
为减函数,
∴当![]() 时,y为增函数,
时,y为增函数,
当![]() 时,y为减函数,
时,y为减函数,
∴![]() 的最大项为
的最大项为![]() 。……………………11分
。……………………11分
又当n=2时,![]() ,
,
当n=3时,![]() ,
,
当n=4时,![]() ,
,
∵![]() ,
,
∴n=3时,![]() 最小。
最小。
∴![]() 的最小项为
的最小项为![]() 。……………………13分
。……………………13分
(文)(Ⅰ)同理科21(Ⅰ)
(Ⅱ)设双曲线的中心为(![]() ),
),
∵a=2,∴![]() …………6分
…………6分
且准线方程为x=0,
∴![]() ,……………………8分
,……………………8分
∴![]() 。
。
由(Ⅰ)知
![]() ,
,
∴![]() ……11分
……11分
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴半虚轴长的取值范围是![]() ………13分
………13分
(如有其它解法请酌情给分)
