朝阳区高三数学第二次统一练习试卷 （理工农医类）

2002．5

 

（考试时间120分钟，满分150分）

参考公式：

三角函数积化和差公式

正棱锥、圆锥侧面积公式：

其中c表示底面周长，l表示斜高或母线长。

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷（选择题共60分）

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡上将该选项涂黑。

（1）设全集

I={-2，-1，，，，1，2，3}，

A={，，1，2，3}，

B={-2，2}

则集合{-2}等于（）

（A）　　 （B）A∩B

 (C)　　(D)

（2）直线 与直线所成的角的大小是（）

（A）　　　 （B）　　

（C）　　（D）

（3）是a<-1成立的（）

（A）充分不必要条件　　

（B）必要不充分条件

（C）充分且必要条件　　

（D）既不充分不必要条件

（4）已知圆锥的体积为，中截面面积为π，则圆锥的侧面积为（）

（A）　　 （B）　　

（C）　 （D）

（5）函数　的反函数是（）

（A）　　

（B）

（C）　

 (D)

(6)若幂函数满足f(2)=4，那么函数的图象为（）

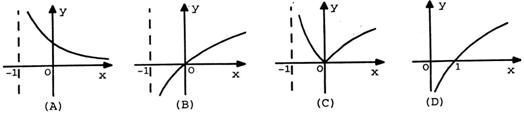
（7）如图，正四面体S—ABC中，D为SC的中点，则BD与SA所成角的余弦值是（）

（A）　　　 （B）

（C）　　　　（D）

（8）函数周期为（）

（A）π　　　 (B)

（C）2π 　　（D）3π

（9）某单位准备用不同花色的装饰石材分别装饰办公楼中的办公室、走廊、大厅的地面及楼的外墙。现有编号为1——6的6种不同花色石材可选择，其中1号石材有微量的放射性，不可用于办公室内，则不同的装饰效果可有

（A）350种　　（B）300种　　

（C）65种　 （D）50种

（10）已知椭圆右焦点为F，Q、P分别为椭圆上和椭圆外一点，且点Q分FP的比为1：2，则点P的轨迹方程为（）

（A）　 　

（B）

（C）　　

（D）

（11）已知是递增数列，且对任意n∈N都有恒成立，则实数λ的取值范是（）

（A）（+∞）　　（B）（0，+∞）

（C）（-2，+∞）　　 （D）（-3，+∞）

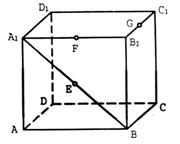
（12）已知棱长为1的正方体容器ABCD——中，在、、的中点E、F、G处各开有一个小孔，若此容器可以任意放置，则装水较多的容积是（小孔面积对容积的影响忽略不计）（）

（A）　　  （B）　

（C）　　　　（D）

第Ⅱ卷（非选择题）

二、填空题：本大题共4个小题，每小题4分，共16分，把答案写在题中横线上。

（13）二项式的展开式中，第3项的系数为_____________。

（14）已知数列的通项公式为，，则

。

（15）右焦点为F的椭圆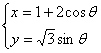（θ为参数）内有一点P（2，1），M为椭圆上一点，则MP+2MF的最小值为_______________.

（16）设K是由函数y=f(x )上任意两点连线的斜率组成的集合，试写出K是区间（0，1）时的一个函数______________（写出一个函数即可，不必考虑全部）。

三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。

（17）（本小题满12分）

已知函数f(x)=sin(x+θ)+cos(x-θ)的定义域为R。

（Ⅰ）当θ=0时，求f(x)的单调增区间；

（Ⅱ）若θ∈（0，π），且sinx≠0，当θ为何值时，f(x)为偶函数。

（18）（本小题满分12分）

设、，且。

（Ⅰ）若，，求和的值；

（Ⅱ）若，且，

求的最小值 。

（19）（本小题满分12分）

如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a，DC=a，F、G分别为EB和AB的中点。

（Ⅰ）求证：FD∥平面ABC；

（Ⅱ）求证：AF⊥BD；

（Ⅲ）求二面角B-FC-G的正切值。

（20）（本小题满分12分）

一种化工产品的单价随着其纯度的提高而提高，某化学公司计划要用单价为A元/千克的原料100千克进行提纯。每次提纯后产品的总价值按如下方法计算：每提纯一次，产品的重量将减少2%，随着产品纯度的提高，提纯后产品的“初步单价”（即未扣除加工费时的“单价”）是提纯前单价的1.3倍，在此计算结果的基础上每提纯一次需要扣除的加工费用是本次提纯前总价值的7.4%（注：本次提纯后的总价值=本次提纯后的重量×本次提纯后的单价）。

（Ⅰ）问第一次提纯后产品的总价值是多少元？

（Ⅱ）求使这种产品总价值翻一番的最小提纯次数n的值

（参考数据：lg2=0.3010，lg3=0.4771）。

（21）（本小题满分13分）

如图，已知动直线l经过点P（4，0），交抛物线于A、B两点，坐标原点O为PQ的中点，

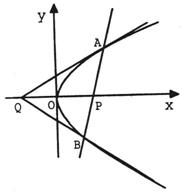
（Ⅰ）求证：∠AQP=∠BQP；

（Ⅱ）当m=2时，是否存在垂直于x轴的直线l′被以AP为直径的圆截得的弦长恒为定值？若存在，求出l′的方程；若不存在，请说明理由。

（22）（本小题满分13分）

已知函数f(t)满足对任意实数x、y都有f(x+y)=f(x)+f(y)+xy+1，且f(-2)=-2.

（Ⅰ）求f(l)的值；

（Ⅱ）证明：对一切大于1的正整数t，恒有f(t)>t

（Ⅲ）试求满足f(t)=t的整数t的个数，并说明理由。

高三数学第二次统一练习参考答案及评分标准　2002、5

一、选择题：

1.A  2.C　 3.B　 4.A　 5.D　 6.C　 7.C　 8.A　 9.B　 10.C　11.D　 12.B

二、填空题：

（13）；　

（14）1；

（15）3　

（16） ，等等。

三、解答题：

（17）（1）解：θ=0时，，…………2分

依条件有，…………………………4分

∴，

∴单调增区间为

即对每个k (k∈Z)，f(x)在区间为单调增函数…………6分

（Ⅱ）解：设f(-x)=f(x),

∴sin(-x+θ)+cos(-x-θ)=sin(x+θ)+cos(x-θ)…………………………8分

sin(x+θ)+sin(x-θ)=cos(x+θ)-cos(x-θ)

∴2sinxcosθ=-2sinxsinθ………………………………………………10分

∵sinx≠0,∴cosθ=-sinθ，∴，∴

依条件令k=1，即时，f(x)为偶函数………………………………12分

（18）解：（1）∵，……（文、理）3分

∴……（文）5分

∴………………………………………………（理）5分

（Ⅱ）（理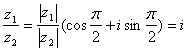）∵……………………7分

∴……9分

∴……11分

当且仅当，即时，取等号，

∴……………………………………12分

（文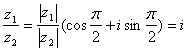）∵………………………………7分

∴……9分

∴…………11分

当且仅当，即cosθ=1时取等号，

∴………………………………12分

（19）（Ⅰ）证：∵F、G分别为EB、AB的中点，∴ 又EA、DC都垂于面ABC，（∴FG⊥面ABC……文2分）∴FG=DC…………（文4分）理2分

∴四边形FGCD为平行四边形，∴FD∥GC，

又，∴FD∥面ABC。……………………（文5分）理4分

（Ⅱ）证：∵AB=EA，且F为EB中点，

∴AF⊥EB　①　又FG∥EA，EA⊥面ABC

∴FG⊥面ABC　∵G为等边△ABC，AB边的中点，∴AG⊥GC…………6分

∴AF⊥GC又FD∥GC，∴AF⊥FD　②

由①、②知AF⊥面EBD，又，∴AF⊥BD…………8分

（Ⅲ）由（Ⅰ）、（Ⅱ）知FG⊥GB,(…文7分)GC⊥GB，∴GB⊥面GCF…………（文9分）

过G作GH⊥FC，垂足为H，连HB，∴HB⊥FC

∴∠GHB为二面角B-FC-G的平面角。……………………（文、理）10分

易求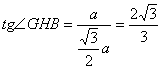，∴……………………（文、理）12分

（20）解（Ⅰ）设第一次提纯后产品的总价值为元，…………2分

∴

元……5分

（Ⅱ）设第n次提纯后产品的总价值为元。其中为第n次提纯后产品的重量，为n次提纯后产品的单价。

则…………7分

∵，，

∴……9分

依条件有，即，

∴……11分

∵n∈N，∴n≥4，即n的最小值为4……………………12分

（21）（Ⅰ）（理）证：设，），B（，），∵O为PQ中点，

∴①但当l⊥x轴时，由抛物线的对称性可知∠AQP=∠BQP…………2分

  ②当l不垂直于x轴时，设l：y =k(x-4) (k≠0),

由，得……………………4分

∴　

∵，同理，

∴………………6分

∴即tg∠AQP=-tg(∠BQP)，∴∠AQP=∠BQP……7分

（文）证：①当l不垂直于x轴时，设l的方程为y=k(x-4),

由得……2分

设，），B（，），

∴

∴　

∴………………4分

，即 ∴AO⊥BO…………5分

②当l⊥x轴时，∵，，∴

 ∴AO⊥BO…………………………7分

（Ⅱ）解：设AP的中点为C，垂直于x轴的直线l′的方程为x=a，

以AP为直径的圆交l′于D、E两点，DE的中点为H。

∵，

  ，

∴……9分

……………………11分

∴令a=3，则对任意满足条件的，都有（与无关），

即为定值。

∴所求直线l′存在，其方程为x=3…………13分

（22）解：（Ⅰ）令x=y=0,得f(0)=-1

令x=y=-1, ∵f(-2)=-2, ∴f(-1)=-2………………2分

令x=1,y=-1, ∴f(0)=f(1)+f(-1),即f(1)=1…………3分

（Ⅱ）令x=1, ∴f(y+1)=f(y)+y+2

即f(y+1)-f(y)=y+2　　 ※……………………（文5分）

∴当y∈N时，有f(y+1)-f(y)>0…………（文7分）理5分

由f(y+1)>f(y), f(1)=1可知，

对一切正整数y都有f(y)>0……………………（文9分）理7分

∴当y∈N时，f(y+1)=f(y)+y+2=f(y)+1+y+1>y+1（文12分）

于是对于一切大于1的整数t，恒有f(t)>t………………………（文13分）理9分

（Ⅲ）由※及（Ⅰ）可知f(-3)=-1, f(-4)=1………………10分

（下面证明当整数t≤-4时，f(t)>t）

∵t≤-4, ∴-(t+2)≥2>0 由※得f(t)-f(t+1)= -(t+2)>0,

即f(-5)-f(-4)>0,同理f(-6)-f(-5)>0,…，

f(t+1)-f(t+2)>0, f(t)-f(t+1)>0，将诸不等式相加得

f(t)>f(-4)=1>-4　∵t≤-4, ∴f(t)>t………………12分

综上，满足条件的整数只有t=1,-2.………………13分

（如有其它解法请酌情给分）