浙江东阳中学02-03年下学期高二数学期中考试
一、选择题(每小题4分)
1.下列方程中表示相同曲线的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.直线![]() 的倾斜角是( )
的倾斜角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.点P(2,-2)及圆![]() 上一动点Q,则PQ最小值是( )
上一动点Q,则PQ最小值是( )
A.37
B.![]() C.3
D.1
C.3
D.1
4.两焦点的坐标是(-2,0)和(2,0),并且经过点P(![]() 的椭圆方程为( )
的椭圆方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
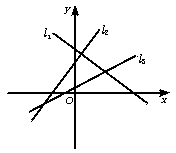 5.若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
5.若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.不等式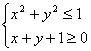 表示平面区域的面积是( )
表示平面区域的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知椭圆![]() 的两个焦点为F1和F2,若椭圆上一点P,P到左准线的距离为2.5,则P到右焦点的距离为( )
的两个焦点为F1和F2,若椭圆上一点P,P到左准线的距离为2.5,则P到右焦点的距离为( )
A.10
B.8
C.![]() D.
D.![]()
8.与双曲线![]() 有共同的渐近线,且经过(2,2)的双曲线方程为( )
有共同的渐近线,且经过(2,2)的双曲线方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.已知圆M:![]() 与y轴相交于A、B,圆心为M,若∠AMB=
与y轴相交于A、B,圆心为M,若∠AMB=![]() ,则m等于( )
,则m等于( )
A.-3
B.![]() C.3
D.8
C.3
D.8
10.已知点A(2,-3),B(-3,-2),若直线l过点P(1,1)且与线段AB相交,则l的斜率上的范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.到定点A(5,0)及定直线l:![]() 的距离之比为5﹕4的轨迹方程是( )
的距离之比为5﹕4的轨迹方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.若点P(m,n)在圆![]() 上运动,则点Q(m+n,2mn)的轨迹方程是( )
上运动,则点Q(m+n,2mn)的轨迹方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每小题3分)
13.若![]() 表示双曲线,则m的取值范围是
.
表示双曲线,则m的取值范围是
.
 14.直线x-2y+2=0绕点(-2,0)逆时针旋转
14.直线x-2y+2=0绕点(-2,0)逆时针旋转![]() 所得的直线方程为
.
所得的直线方程为
.
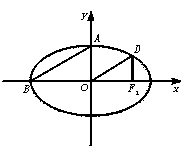
15.如图A、B是椭圆的顶点,O是中心,F1是右焦点,D是椭圆上一点且DF1⊥BO,AB∥DO,则其离心率为 .
16.点P(8,1)平分双曲线x2-4y2=4的一条弦,则这条弦所在的直线方程是 .
三、解答题(每小题8分)
17.△ABC的三个顶点A(-3,0)、B(2,1)、C(-2,3),求①BC边的中线AD所在直线方程;②BC边的垂直平分线DE的方程.
18.下表为X、Y、Z三种食品的维生素,含量及成本
| X | Y | Z | |
| 维生素A(单位/kg) | 400 | 600 | 400 |
| 维生素B(单位/kg) | 800 | 200 | 400 |
| 成本(元/kg) | 6 | 5 | 4 |
某人欲将X、Y、Z三种食品混合成100kg的混合物,要求混合物至少含有44000单位维生素A和48000单位的维生素B,问采用何种配比成本最低.
19.直线l:y=2x+b和两定直线l:2x-3y+1=0,l2:x+4y-5=0,分别交于点A、B,在b变化的情况下,求线段AB中点的轨迹方程.
20.已知一圆与y轴相切,在直线y=x上截得的弦长为![]() ,圆心在直线
,圆心在直线![]() 上,求此圆的方程.
上,求此圆的方程.
21.已知椭圆以双曲线![]() 的焦点为焦点,直线y=4是椭圆的一条准线.
的焦点为焦点,直线y=4是椭圆的一条准线.
①求椭圆的方程;
②又设点P在椭圆上,且![]() .
.
