湖 北 省 十 一 校 大 联 考
数 学 试 题
![]()
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试用时120分钟。
第Ⅰ卷 (选择题 共60分)
一、选择题:a
(本大题共12小题,每小题5分共 60分,在每小题的四个选项中,只有一项是符合题目要求的)
1.设集合A =![]() , B=
, B=![]() ,则A∩B= ( )
,则A∩B= ( )
A. ![]() B.
B.![]()
C. ![]() D.
D.
![]()
2.在锐角三角形ABC中设x = (1+sinA) (1+sinB) , y = (1+cosA) (1+cosB) ,则x 、y大小关系为 ( )
A.x≤y B.x < y C.x≥y D.x > y
3.下列不具有周期性的函数是 ( )
A.f (x) = 3 B.f (x) = lg sinx
C.f (x) = sinπx +cos x D.f (x) = (-1)x (x∈z)
4.已知圆C1:
x2 + y2 + 2x-2y + 1 = 0,圆C2: x2 + y2-4x-2y +1 = 0.圆心分别为C1,C2,两圆外公切线交于点P,若![]() = λ
= λ![]() 则λ等于
( )
则λ等于
( )
A.![]() B.-
B.-![]() C.-2
D. 2
C.-2
D. 2
5.在边长为1的等边三角形ABC中,设![]() =
= ![]() ,
,![]() =
= ![]() ,
,![]() =
= ![]() ,则
,则
![]() ·
·![]() +
+![]() ·
·![]() +
+![]() ·
·![]() 等于
( )
等于
( )
|
6.根据科学测算,运载神舟六号飞船的长征系列火箭,在点火后一分钟上升的高度为1km,以后每分钟上升的高度增加2km,在达到离地面240km高度时船箭分离,则从点火到船箭分离大概需要的时间是 ( )
A.20分钟 B.16分钟 C.14分钟 D.10分钟
7.函数f (x) = lg (![]() )的值域是R,则
)的值域是R,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
8.数列![]() 满足
满足 若
若![]() 则
则![]() 的值为
( )
的值为
( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
9.(文)定义在R上的偶函数y = f (x )满足f ( x+2 ) = ![]() f (x )对所有实数x都成立,且在[
f (x )对所有实数x都成立,且在[![]() 2,0 ]上单调递增,
2,0 ]上单调递增,![]() 则下列成立的是 ( )
则下列成立的是 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
(理)![]() 的定义域为
的定义域为![]() 则实数
则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.若把一个函数y =f (x)的图像按![]() 平移后得到函数y = cosx的图像, 则y = f (x)的解析式是 ( )
平移后得到函数y = cosx的图像, 则y = f (x)的解析式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
11.直线![]() 与圆
与圆![]() 切于点P
切于点P![]() ,则
,则![]() 的值为
( )
的值为
( )
A.![]() B.1
C.
B.1
C.![]() D.3
D.3
![]() 12.实系数方程
12.实系数方程![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() 则
则![]() 的
的
取值范围是 ( )
|
第Ⅱ卷(非选择题 共90分)
二、填空题:
(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)
13.函数f (x) = ![]() 的定义域是
的定义域是
14.双曲线![]() +
+![]() =1的离心率e = 2 ,则k的值为
=1的离心率e = 2 ,则k的值为
15.设函数y = f (x)存在反函数且y = f ( x +3 )过点A (1 , 2 ) , 则y = f -1 (x+3)的 反函数必经过的点的坐标是
16.设PQ是抛物线 y2 = 2px(p>0)上过焦点F的一条弦,L是抛物线的准线,给定下列命题:①以PF为直径的圆与y轴相切 , ②以QF为直径的圆与y轴相切, ③以PQ为直径的圆与准线L相切, ④以PF为直径的圆与y 轴相离 , ⑤以QF为直径的圆与y轴相交, 则其中所有正确命题的序号是:
三、解答题. (本大题共6个小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本题12分)已知f (x ) =
2cos2x +2![]() sinx cosx + a
(a为常数)
sinx cosx + a
(a为常数)
 (1)求f (x)的最小正周期 (2)求f (x)的单调递增区间
(1)求f (x)的最小正周期 (2)求f (x)的单调递增区间
(3)若f (x)在[![]() ,
, ![]() ]上最大值与最小值之和为3,求a的值.
]上最大值与最小值之和为3,求a的值.
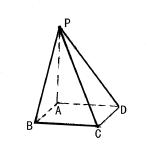
18.(本题12分)在四棱锥P-ABCD中,底面ABCD是边长为a的正方形, PA⊥平面ABCD,且PA = 2AB.
(1)求证:平面PAC⊥平面PBD
(2)求二面角B- PC - D的大小
19.(本题12分)设a为常数f (x ) = ![]() , 如果对 任意x∈R,不等式f (x ) + 4
≥0恒成立,求实数a的取值范围.
, 如果对 任意x∈R,不等式f (x ) + 4
≥0恒成立,求实数a的取值范围.
20.(本题12分)刘先生购买了一部手机,欲使用中国移动的“智慧”卡或加入中国联通网,经调查收费标准如下:
| 网络 | 月租 | 本地话费 | 长途话费 |
| 甲:联通 | 12元 | 0.3元/分钟 | 0.6元/分钟 |
| 乙:移动 | 无 | 0.5元/分钟 | 0.8元/分钟 |
|
(1)设刘先生每月通话时间为x分钟,求使用甲、乙两种入网方式所需话费的函数
f (x), g (x).
(2)请你根据刘先生每月通话时间为刘先生选择一种较为省钱的入网方式.
21.(本题12分)(文)已知函数f (x)
= a·bx的图像过点A(1, ![]() ), B (2 ,
), B (2 , ![]() )
)
(1 ) 求函数f ( x ) 的解析式.
(2)设![]() , n∈N+, Sn 是数列
, n∈N+, Sn 是数列![]() 前n项和,求S20.
前n项和,求S20.
(3)在(2 )的条件下,若 ![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(理)已知数列![]() 中各项为:
中各项为:
|
|
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn .
22.(本题14分)(文)已知A、B、D三点不在一条直线上,且A(-2 ,0) ,
B(2 ,0),![]() = 2 ,
= 2 ,![]()
(1)求点E的轨迹方程;
(2)过点A作直线L交以A、B为焦点的椭圆于M、N两点。线段MN的中点到y轴距离为![]() 且直线MN与点E的轨迹相切,求椭圆的方程.
且直线MN与点E的轨迹相切,求椭圆的方程.
(理)在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①![]() , ②
, ②![]() =
= ![]() =
= ![]() ③
③![]() ∥
∥![]()
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(![]() , 0) ,已知
, 0) ,已知![]() ∥
∥![]() ,
, ![]() ∥
∥![]() 且
且![]() ·
·![]() = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
|
参 考 答 案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | D | C | B | A | B | C | C | B | D | D | A |
二、填空
13.![]() 14. -12 15. (4 ,-1) 16.①②③
14. -12 15. (4 ,-1) 16.①②③
简析:2.![]() sinA>cosB,
sinB>cosA
sinA>cosB,
sinB>cosA ![]()
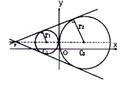 4.圆C1:(x
+ 1)2 + (y-1)2 = 1 , 圆C2:(x-2)2 + (y-1)2 = 4,
4.圆C1:(x
+ 1)2 + (y-1)2 = 1 , 圆C2:(x-2)2 + (y-1)2 = 4,
两圆外切 如图可知PC1 = C1C2 = 3
![]()
![]() 故选B
故选B
7.令t =3x+3-x-a 则tmin=2-a≤0 ![]() a ≥2
a ≥2
9.(文)由f (x+2) = -f (x) 有f (x + 4) = f
(x) ![]() T = 4
T = 4
而f (x)在R上为偶函数又在[-2,0]上单调递增,所以f (x)在[0,2]上单调递减
![]() ,
, ![]() ,
, ![]()
![]()
![]() 故选B
故选B
9.(理)由3 + a·![]() ≥0 a·
≥0 a·![]() ≥-3
≥-3
当a≥0时定义域为R不合条件 ![]() a < 0
a < 0
x≤![]()
![]()
![]() = 2 ,
= 2 , ![]() a =
a = ![]()
12.设f (x) = x2 + ax + 2b,方程x2 + ax +2b = 0两根满足 0 < x1 < 1< x2 < 2的充要条件
 是
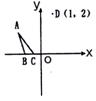
是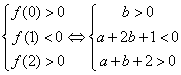 记A(-3,1) B(-2,0)
记A(-3,1) B(-2,0)
C(-1,0)则动点(a , b)表示△ABC内部的点集;而![]()
表示点(a ,b)与D(1 ,2)连线的斜率
KAD = ![]() , KCD = 1
, KCD = 1 ![]() 故选 A
故选 A
15.由已知得2 = f (4) , ![]() 4 =
4 = ![]() (2 ) ,
(2 ) , ![]() y =
y = ![]() (x + 3 )过点(-1,4)
(x + 3 )过点(-1,4)
所以 y =![]() (x + 3)的反函数过点(4,-1)
(x + 3)的反函数过点(4,-1)
三、解答题
17.解:f (x) =![]() sin2 x + cos2 x + a + 1 = 2sin (2 x +
sin2 x + cos2 x + a + 1 = 2sin (2 x +![]() ) + a +1……………………(2分)
) + a +1……………………(2分)
(1)T = π…………………………………………………………………………… (4分)
(2)由2kπ-![]() ≤2x +
≤2x +![]() ≤2 kπ+
≤2 kπ+![]() 得kπ-
得kπ-![]() ≤x≤kπ+
≤x≤kπ+![]()
![]() f (x)单调递增区间为[kπ-
f (x)单调递增区间为[kπ-![]() , kπ+
, kπ+![]() ] (k∈ z ) ……………………………(8分)
] (k∈ z ) ……………………………(8分)
(3)由(2)知f (x)在[-![]() ,
,![]() ]为增函数
]为增函数
![]() f (
f (![]() ) + f (-
) + f (-![]() ) = 3
) = 3
![]() a = 0 ……………………………………………………………………………(12分)
a = 0 ……………………………………………………………………………(12分)
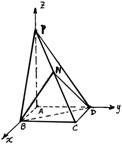 18. 解:(1)证明:
18. 解:(1)证明:![]() PA⊥平面ABCD
PA⊥平面ABCD![]() PA⊥BD
PA⊥BD
![]() ABCD为正方形
ABCD为正方形 ![]() AC⊥BD
AC⊥BD
![]() BD⊥平面PAC 又 BD在平面BPD内,
BD⊥平面PAC 又 BD在平面BPD内,
![]() 平面PAC⊥平面BPD ……………………(6分)
平面PAC⊥平面BPD ……………………(6分)
(2)解法一:在平面BCP内作BN ⊥ PC垂足为N,
连DN, ![]() Rt△PBC≌Rt△PDC,
由BN⊥PC得DN⊥PC;
Rt△PBC≌Rt△PDC,
由BN⊥PC得DN⊥PC;
![]() ∠BND为二面角B- PC-D的平面角.
∠BND为二面角B- PC-D的平面角.
在△BND中,BN = DN = ![]() a ,BD =
a ,BD =![]() a
a
![]() cos∠BND =
cos∠BND = 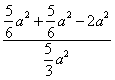 =
= ![]() …………………………………(10分)
…………………………………(10分)
![]() 二面角B-PC-D大小为π- arc cos
二面角B-PC-D大小为π- arc cos ![]() . (或arc cos (
. (或arc cos (![]() )) …………(12分)
)) …………(12分)
解法二:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间坐标系如图
在平面BCP内作BN⊥PC垂足为N连DN
|
|
![]() ∠BND为二面角B-PC-D的平面角………………………………(8分)
∠BND为二面角B-PC-D的平面角………………………………(8分)
设![]() ,
,![]()
![]()
![]() BN⊥PC
BN⊥PC ![]()
即 ![]()
![]()
![]() ,
,![]() ………………………(10分)
………………………(10分)
![]() cos∠BND =
cos∠BND =![]() =
=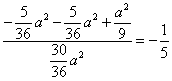
![]() 二面角B-PC-D大小为
二面角B-PC-D大小为![]() - arccos
- arccos![]() ……………………………………(12分)
……………………………………(12分)
解法三:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴,建立如图空间坐标系,作AM⊥PB于M、AN⊥PD于N,易证AM⊥平面PBC、AN⊥平面PDC,
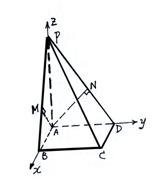 设
设![]()
![]()
![]()
![]()
![]()
![]()
![]() AM⊥PB,
AM⊥PB, ![]() ·
·![]() = 0
= 0
![]()
![]() =
= ![]()
![]() , 同理
, 同理 ![]()
cos∠MAN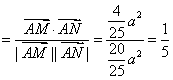 ………………………………………(10分)
………………………………………(10分)
![]() 二面角B-PC-D大小为
二面角B-PC-D大小为![]() -arc cos
-arc cos![]() ……………………………………(12分)
……………………………………(12分)
|
19.
解: f (x) + 4≥0![]() cos2x - (a2-3a)cosx-3≤0
cos2x - (a2-3a)cosx-3≤0
设t = cosx则-1≤t≤1
![]() g (t) = t2-(a2-3a)t-3≤0 对-1≤t≤1所有t都成立. ………… (4分)
g (t) = t2-(a2-3a)t-3≤0 对-1≤t≤1所有t都成立. ………… (4分)
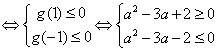 …………………………………………(8分)
…………………………………………(8分)
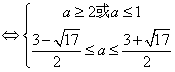 ………………………………………………(10分)
………………………………………………(10分)
![]() 或
或![]() ……………………………………(12分)
……………………………………(12分)
解法二:
同解法一得:g (t) = t2-(a2-3a) t-3≤0对-1≤t≤1的所有t均成立……(4分)
则当![]() ≥0即a≥3或a≤0时,g (-1)≤0
≥0即a≥3或a≤0时,g (-1)≤0
a2-3a-2≤0 , ![]() ≤a≤
≤a≤![]()
![]() 3≤a≤
3≤a≤![]() 或
或![]() ≤a≤0 ………………………………(7分)
≤a≤0 ………………………………(7分)
当![]() <0即0 < a < 3时,g (1)≤0
<0即0 < a < 3时,g (1)≤0
a2-3a + 2≥0 ,a≥2或 a≤1 ![]() 0 < a≤1或2≤a < 3 …………………(10分)
0 < a≤1或2≤a < 3 …………………(10分)
综合得![]() ≤a≤1或2≤a≤
≤a≤1或2≤a≤![]() ………………………………… (12分)
………………………………… (12分)
20
解:(1)因刘先生本地电话时间为长途电话的5倍,所以本地通话时间与长途通话时间分别为![]() ,
, ![]() . ……………………………………………………………(2分)
. ……………………………………………………………(2分)
|
![]() f ( x ) = 0.35 x + 12 ………………………………………………………… (4分)
f ( x ) = 0.35 x + 12 ………………………………………………………… (4分)
g ( x ) = 0.5×![]() + 0.8×
+ 0.8×![]()
![]() g ( x )=0.55 x
………………………………………………………………(6分)
g ( x )=0.55 x
………………………………………………………………(6分)
(2 ) ![]() g ( x )-f ( x ) = 0.2x-12 = 0.2 (x-60)
g ( x )-f ( x ) = 0.2x-12 = 0.2 (x-60)
①当x > 60时,g ( x ) > f (x ) 刘先生采用联通网络较省钱。 ………………(8分)
②当0 < x < 60时, g ( x ) < f ( x ) 刘行生采用移动网络较省钱。 ……(10分)
③当x = 60时 g (x ) = f ( x ) 刘先生任选其中一种均可 ……………………(12分)21。解:(文)(1)因图像过点A(1,![]() ), B(2,
), B(2, ![]() )
)
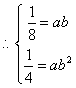
解之得 a = ![]() , b = 2 …………………………………………………………(2分)
, b = 2 …………………………………………………………(2分)
![]() f (x) ==
f (x) == ![]() ……………………………………………………… (4分)(2)
……………………………………………………… (4分)(2)![]()
![]() 是首项为-3公差为1的等差数列………………………………………(6分)
是首项为-3公差为1的等差数列………………………………………(6分)
![]() Sn = -3n+
Sn = -3n+![]() =
= ![]() n (n-7)
n (n-7)
![]()
![]() = 130 …………………………………………………………………(8分)
= 130 …………………………………………………………………(8分)
(3)![]()
Tn = -3·![]() + (-2)· (
+ (-2)· (![]() )2 + …… + (n- 4) (
)2 + …… + (n- 4) (![]() ) n
…………①
) n
…………①
![]()
![]() Tn = (-3)· (
Tn = (-3)· (![]() )2 + …… + (n-5) (
)2 + …… + (n-5) (![]() ) n + (n-4 ) (
) n + (n-4 ) (![]() )n+1
……②
)n+1
……②
①-②得:![]() Tn = -3·
Tn = -3·![]() + (
+ (![]() )2 + …… + (
)2 + …… + (![]() )n-(n-4) (
)n-(n-4) (![]() )n+1
)n+1
|
(理)(1)![]() ……………………………… (2分 )
……………………………… (2分 )
![]()
![]() …………………………………(4分)
…………………………………(4分)
|
![]()
![]() = A (A+1) , 得证 ………………………………………………………( 6分) (2)
= A (A+1) , 得证 ………………………………………………………( 6分) (2) ![]() ………………………………………………… (8分)
………………………………………………… (8分)
![]()
![]() ……………………………………………(12分)
……………………………………………(12分)
22.。解:(文)(1)设E ( x , y ),
![]()
![]()
又![]()
![]() x2+ y2 = 1 (y≠0) ………………………………………………………… (6分)
x2+ y2 = 1 (y≠0) ………………………………………………………… (6分)
(2)设椭圆方程为:![]() , 直线L:y = k (x + 2)
, 直线L:y = k (x + 2)
由于直线L与圆E相切,![]()
![]() ,
,![]()
![]()
|
![]()
![]()
![]()
![]() 5 a2 =
6 b2 + 2 a2 ,
5 a2 =
6 b2 + 2 a2 , ![]() a2 = 2
b2 ………………(12分)
a2 = 2
b2 ………………(12分)
又c 2 =
4 ![]() b2 = 4
, a2 = 8 椭圆方程为
b2 = 4
, a2 = 8 椭圆方程为![]() …………………(14分)
…………………(14分)
(理)(1)设C ( x , y ), ![]()
![]() ,由①知
,由①知![]() ,
,![]() G为
△ABC的重心 ,
G为
△ABC的重心 , ![]() G(
G(![]() ,
,![]() ) …………………………………………(2分)
) …………………………………………(2分)
由②知M是△ABC的外心,![]() M在x轴上
M在x轴上
由③知M(![]() ,0),
,0),
由![]() 得
得![]()
化简整理得:![]() (x≠0 )………………………………………… (6分)
(2)F(
(x≠0 )………………………………………… (6分)
(2)F(![]() ,0 )恰为
,0 )恰为![]() 的右焦点
的右焦点
设PQ的斜率为k≠0且k≠±![]() ,则直线PQ的方程为y = k ( x -
,则直线PQ的方程为y = k ( x -![]() )
)
由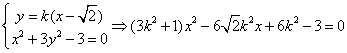
设P(x1
, y1) ,Q (x2 ,y2
) 则x1 + x2 = ![]() , x1·x2 =
, x1·x2 =![]() …… (8分)
…… (8分)
|
= ![]() ·
·![]()
= ![]()
![]() RN⊥PQ,把k换成
RN⊥PQ,把k换成![]() 得 RN =
得 RN = ![]() ………………………( 10分)
………………………( 10分)
![]() S =
S =![]() PQ · RN
PQ · RN
=![]()
=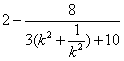 )
)
![]()
![]() ≥2 ,
≥2 , ![]() ≥16
≥16
![]() ≤ S < 2 , (当 k = ±1时取等号) ……………………………………(12分)
≤ S < 2 , (当 k = ±1时取等号) ……………………………………(12分)
又当k不存在或k = 0时S = 2
综上可得 ![]() ≤ S ≤ 2
≤ S ≤ 2
![]() Smax = 2 , Smin =
Smax = 2 , Smin = ![]() ……………………………………………………… (14分)
……………………………………………………… (14分)
|