广西部分重点中学

2005—2006学年度上学期高三年级联合考试

数学（理科）

YC

本试卷分第Ⅰ（选择题）和第Ⅱ卷（非选择题）两部分．

第I卷（60分）

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是最符合题目要求的。

1．与直线垂直的直线的倾斜角为　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　D．

2．已知的值　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．－　　　　　　　　　 C．－　　　　　　　　　D．

3．已知α、β是不同的两个平面，直线aα，直线bβ，命题p:a与b无公共点；命题

　 q:a//β，则p是q的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．充分而不必要的条件　　　　　　　　　　　　　B．必要而不充分的条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要的条件

4．设，则锐角α为　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．30°　　　　　　　　　 B．60°　　　　　　　　　 C．45°　　　　　　　　　 D．75°

5．10张奖券中只有3张有奖，5个人购买，至少有1人中奖的概率是　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　　　D．

6．已知f(x)是R上的偶函数，对x∈R都有f(x+6)=f(x)+f(3)成立，若f(1)=2，则f(2005)等于

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．2005　　　　　　　　　 B．2　　　　　　　　　　　　C．1　　　　　　　　　　　　D．0

7．反函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．YCY　　　 B．

　　　 C．　　　　　　　D．

8．在等数列{a_n}中，满足3a₄=7a₇, 且a₁>0，若S_n取得最大值，则n=　　　　　　　　　　 （　　）

　　　 A．6　　　　　　　　　　　　B．7　　　　　　　　　　　　C．8　　　　　　　　　　　　D．9

9．设函数f(x)=a^－x(a>0, 且a≠1)，f(2)=4，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．f(－2)>f(－1)　　　B．f(－1)>f(－2)　　　C．f(1)>f(2)　　　　　　 D．f(－2)>f(2)

10．函数y=f(x)的图像如图甲所示，则函数y=f(1－x)的图像可能是　　　　　　　　　　　　（　　）

11．在2与7之间插入n个数，使这个以2为首项的数列成等差数列，并且S₁₆=56，则n=

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．23　　　　　　　　　　　B．24　　　　　　　　　　　 C．25　　　　　　　　　　　D．26

12．一张报纸的厚度为a，面积为b，现将报纸对折（即沿对边中点连线折叠）7次，这时报纸的厚度和面积分别为YCY　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　 B．　　　　　C．　　　 D．

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题4分，共16分，把答案填题中横线上。

13．函数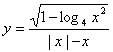的定义域为　　　　　　  ；

14．函数的单调递减区间是　　　　　   

15．在R上定义运算：xy=x(1－y)，若不等式(x－a) (x+a)<1对任意实数x恒成立，则实数a的取值范围是　　　　   

16．在等差数列{a_n}与等比数列{b_n}中，a₁=b₁>0，a_2n+1=b_2n+1>0(n=1,2,3,…)则a_n+1与b_n+1的大小关系是　　　　　  .

三、解答题：（本大题共6小题，满分74分。解答应写出文字说明证明过程或演算步骤）

17．（12分）已知集合.

　 （1）当a=2时，求A∩B；

　 （2）求使BA的实数a的取值范围.

18．（12分）已知等比数列{a_n}，a₅－a₁=15, a₄－a₂=6, a_n>0；

　 （1）求{a_n}的通项公式；

　 （2）令b_n=2·log₂a_n+3，求数列{b_n}的前n项和S­_n。

19．（12分）设函数的图象关于直线y=x对称.

　 （1）求m的值；

　 （2）若直线y=a(a∈R)与f(x)的图象无公共点，且，求实数t的取值范围.

20．（12分）某家用电器厂根据其产品在市场上的销售情况，决定对原来以每件2000元出售的一种产品进行调价，并按新单价的八折优惠销售。结果每件产品仍可获得实际销售价20%的利润。已知该产品每件的成本是原销售价的60%。

（1）求调价后这种产品的新单价是每件多少元？让利后的实际销售价是每件多少元？

（2）为使今年按新单价让利销售后的利润总额不低于20万元，今年至少应销售这种产品多少件？（每件产品利润=每件产品的实际销售价一每件产品的成本价）

21．（12分）设数列{a_n}的前n项和为S_n，已知a₁=1，且满足3

　 （1）求证：为等差数列

　 （2）设

22．（14分）设函数y=f(x)的定义域为（0，+∞），且对任意的正实数x, y，均有

f(xy)=f(x)+f(y)恒成立.已知f(2)=1，且当x>1时，f(x)>0。

　 （1）求f(1), f()的值；

　 （2）试判断y=f(x)在（0，+∞）上的单调性，并加以证明；

　 （3）一个各项均为正数的数列{a­_n}满足f(S_n)=f(a_n)+f(a_n+1)－1，n∈N*，其中S_n是数列{a_n}的前n项和，求数列{a_n}的通项公式；

　 （4）在（3）的条件下，是否存在正数M，使2ⁿ·a₁·a₂…a_n≥M·.(2a₁－1)·(2a₂－1)…(2a_n－1)对于一切n∈N*均成立？若存在，求出M的范围；若不存在，请说明理由.

数学（理）参考答案

一、选择题：

　　1.B　　2.D　 3.B　 4.C　 5.D　　6.B　　7.B　　8.D　 9.A　 10.D　 11.B　 12.C

二、填空题：

13.;　 14. 　 15. 　　16.

17．解：（1）当a=2时，A=（2，7），B=（4，5）∴A∩B=（4，5）………………3分

　 （2）∵B=（2a,a²+1），当a<时，A=（3a+1，2）………………………………5分

　　　　要使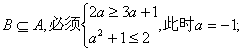……………………………… 7分

　　　　当a=时，A=φ，使BA的a不存在；………………………………… 9分

　　　　当a>时，A=（2，3a+1）

　　　　要使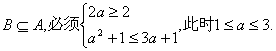…………………………11分

　　　　综上可知，使BA的实数a的取值范围为[1，3]∪{－1}……………… 12分

18．解：（1）设等比数列{a_n}的公比为q，则a_n=a₁q^n－1

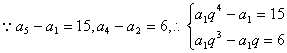………………………………… 1分

由①÷②得：，……………………………………………………… 2分

整理得2q²－5q+2=0，

解得：q=2或q=………………………………………………………………… 3分

当q=时，代入①有a₁=－16（与a_n>0矛盾，舍去）…………………………… 4分

当q=2时，代入①有a₁=1，……………………………………………………… 5分

∴a_n=2^n－1…………………………………………………………………………… 6分

（2）∵b_n=2log₂a_n+3, ∴b_n=2n+1……………………………………………………… 8分

∵b_n+1－b­_n=2(n+1)+1－(2n+1)=2

∴{b_n}是首项为3，公差为2的等差数列，………………………………… 10分

………………………………………………12分

19．解：（1）由…………… 2分

由已知得，………………4分

（2）由（1）知，…………6分

∴由已知得:a=1于是…………………………………………………………8分

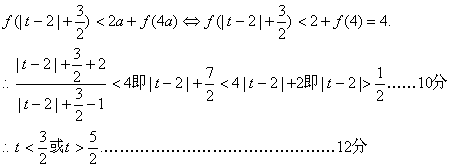
20．解：（1）设每件产品的新单价为x元…………………………………………1分

由已知：该产品的成本是2000×60%=1200元………………………………2分

由题意：x·80%－1200=20%（80%·x）……………………………………3分

解得：x=1875（元）……………………………………………………………4分

∴80%·x=1500元………………………………………………………………5分

所以，该产品调价后的新单价是每件1875元，让利后实际售价为每件1500元.……6分

（2）设今年至少应生产这种电器m件，则由题意，

得m(1500－1200)≥200000…………………………………………………… 8分

解得：m≥666……………………………………………………………… 9分

∵m∈N，∴m的最小值应为667件…………………………………………11分

答：今年至少售出667件产品，才能使利润总额不低于20万元.……… 12分

21．证明：（1）…………2分

………………………………………………………… 4分

所以，公差为3的等差数列………………………………6分

（2）

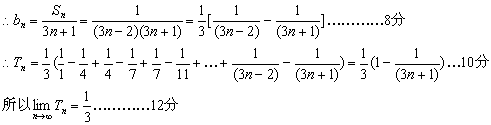
22．解：（1）∵f(2×1)=f(2)+f(1), ∴f(1)=0…………………………………………1分

　 又∵f(1)=f(2×)=f(2)+f(),且f(2)=1，∴f()=－1…………………………2分

（2）设…4分

∴函数y=f(x)在（0，+∞）上是增函数…………………………………………5分

（3）∵f(2)=1, ∴由f(S_n)=f(a_n)+f(a_n+1)－1(n∈N*)，得f(2S_n)=f[a_n(a_n+1)]

∵函数y=f(x)在（0，+∞）上是增函数，

∴2S_n=a_n(a_n+1)………………………………………………………………（1）7分

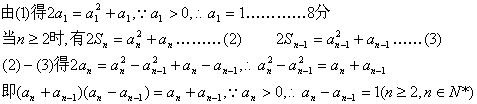
∴数列{a_n}是首项为1，公差为1的等差数列，从而有a_n=n……………………10分

（4）∵a_n=n，故不等式

可化为2ⁿ×1×2×3×…×n≥M×1×3×5×…×（2n－1），

即

则是单调递增……12分

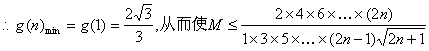对一切n∈N*都成立的正数M的范围是………………………………………………14分