温州市八校联考数学(文科)试卷答案

一、选择题：（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	A	D	C	B	D	C	A	C

二、填空题（本大题共4小题，每小题4分，共16分）

11.　　　　12.　　　[7，68]　

13.　 3/2或2/3 　　　　14.　　7/24　　　　

三、解答题(共84分)

15．(本题满分14分） 已知集合，集合，若，求实数的值.

解：　　　　　　 　 

　　　　　　　　　　　　　　　　　　　　

则有或　　　　   

16.（本题满分14分）且最长边为.

（1）求证：

（2）求△ABC最短边的长．

解（1）　　　　　　　　　　　　　  　　　

　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

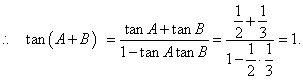
（2）∴ ∠C所对的边最长，∠B所对的边最短，　　　　 

　由，求得，　　　　　　　　　　　　　　  　　　　　 

由正弦定理　　

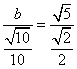
17. （本题满分14分）已知数列的前n项和为

　　　（1）求；　 （2）求数列的通项

解：（1）∵

∴当n=1时，=a₁ ∴a₁=；

当n=2时， ∴

　（2）∵∴

　　　　　　　　　　

 ∴ ∴ 　　又当n=1时，

∴{a_n}为等比数列，且首项与公比都为

∴

18.（本题满分14分）如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，M、N分别为BB₁、B₁C₁的中点，P为线段MN的中点.

　 （1）求DP和平面ABCD所成角的正切；

　 （2）设DP和AC­₁所成角为，求的值.

解：（1）过P作PH⊥BC，垂足为H，连DH

∵面BC₁⊥面AC，PH⊥面ABCD

∴DP和面ABCD所成角即为∠HDP

∵PH=，CH=

∴DH=

∴在Rt△PHD中，tan∠HDP=

　（2）以A₁为原点，A₁B₁为x轴，A₁D₁为y轴，A₁A为z轴建立空间直角坐标系，则A（0，0，1），C₁（1，1，0）

　　　 ∴　　　 D（0，1，1），P（1，，），

∴=（1，－，－）

　　  

19. （本题满分14分）经调查，若干年内某产品关税与市场供应量P的关系允许近似的满足：（其中t为关税的税率，且,x为市场价格，b、k为正常数），当t=时的市场供应量曲线如图

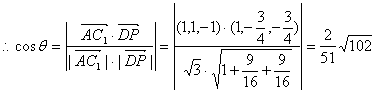
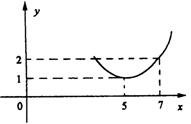
　 （1）根据图象求k、b的值；

　 （2）若市场需求量为Q，它近似满足.

当P=Q时的市场价格称为市场平衡价格.为使市

场平衡价格控制在不低于9元，求税率t的最小

值.

解（1）由图可知，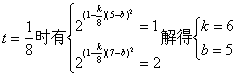

　 （2）当P=Q时，得

　　　　解得　　　　

　　　　

20.（本题满分14分）设函数f(x)=x(x－1)(x－a)(a>1).

　 （1）求导数，并证明f(x)有两个不同的极值点x₁、x₂

　 （2）若不等式f(x₁)+f(x₂)≤0成立，求a的取值范围.

解：（1）=3x²－2(1+a)x+a. 令=0得

　　　　方程3x²－2(1+a)x+a=0.

　　　　因△=4(a²－a+1)≥4a>0，故方程有两个不同实根x₁、x₂，

　　　　不妨设x₁<x₂，由=3(x－x₁)(x－x₂)可判别的符号如下：

　　　　当x<x₁时，>0；当x₁<x<x₂时，<0;

　　　　当x>x₂时，>0.因此x₁是极大值点，x₂是极小值点.

　 （2）因f(x₁)+f(x₂)≤0，

　　　　故得不等式

　　　　即(x₁+x₂)[(x₁+x₂)²－3x₁x₂]－(1+a)[(x₁+x₂)²－2x₁x₂]+a(x₁+x₂)≤0.

　　　　又由（1）知

　　　　代入前面不等式，两边除以（1+a），并化简得2a²－5a+2≥0.

　　　　解不等式得a≥2或a≤（舍去）.因此，当a≥2时，不等式f(x₁)+f(x₂) ≤0成立.