不等式
(山东省郓城第一中学 274700)张钟谊
不等式是中学数学的重点内容,是学习数学其它各部分知识所必不可少的工具,也是历年高考考查的重点内容。
复习提要
因为不等式的性质、不等式的证明、不等式的解法、含有绝对值的不等式是高考考试内容,因此必须:(1)掌握不等式的性质及其证明,掌握证明不等式的几种常用方法,掌握两个和三个(不要求四个和四个以上)正数的算术平均数不小于它们的几何平均数这两个定理。并能运用上述性质、定理和方法解决一些问题;(2)在熟练掌握一元一次不等式(组)、一元二次不等式的解法的基础上,初步掌握其他的一些简单的不等式的解法;(3)会用不等式![]()
例题及评注
例1 (1996年上海高考题)如果![]() ,那么
,那么![]() 间的关系是( )
间的关系是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
解:分别在同一坐标系中作![]() 的图像(如图1)便知应选(B)。
的图像(如图1)便知应选(B)。
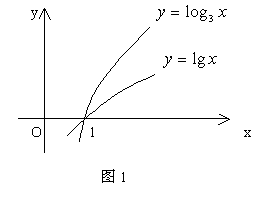
评注:利用特例分析法,并熟练掌握对数函数图像性质是确保解决对数问题的基本保证。
例2 不等式![]() 的解集为__________。(1995年全国高考题)
的解集为__________。(1995年全国高考题)
解:原不等式等价于![]() ,由指数函数
,由指数函数![]() 在R上单调递增可知:
在R上单调递增可知:![]() 。所以原不等式的解集为
。所以原不等式的解集为![]() 。
。
评注:指数函数性质的纯熟运用是解本题的关键。
例3 解不等式![]() (1985年全国高考题)
(1985年全国高考题)
解法1:原不等式等价:
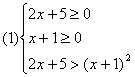
或![]()
解(1)、(2)得原不等式的解集为![]()
解法2:设![]() 且
且![]() ,则
,则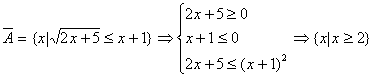 从而解得
从而解得![]() 。
。
评注:对于无理不等式的解法一般采用等价转化为不等式组来处理,注意分类讨论,同时还应采用正难则反的策略求解。
例4 已知![]() ,对于
,对于![]() 的
的![]() 的值都有
的值都有![]() 成立,则对这些
成立,则对这些![]() 的值都有
的值都有![]() 。
。
证明:令![]()
![]()
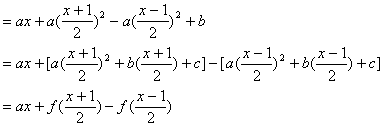
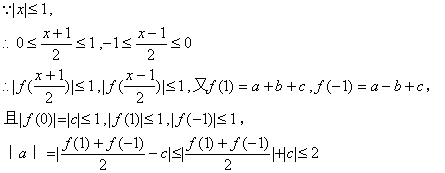
![]()
评注:本例论证突破的关键有两处:一是对![]() 的恒等变形;二是对
的恒等变形;二是对![]() 的恒等变形。在此基础上运用条件及绝对值不等式性质达到证明的目的。近年高考题中的高档题都考查到这些思想方法的运用。
的恒等变形。在此基础上运用条件及绝对值不等式性质达到证明的目的。近年高考题中的高档题都考查到这些思想方法的运用。
例5 已知![]() ,问是否存在正整数
,问是否存在正整数![]() ,使不等式
,使不等式![]() 恒成立?如果存在,求出所有
恒成立?如果存在,求出所有![]() 值;如果不存在,试说明理由。
值;如果不存在,试说明理由。
解:![]() ,
,![]() 原不等式等价于
原不等式等价于![]() ,此式恒成立的充要条件是
,此式恒成立的充要条件是![]()
![]() ,
,![]() 当且仅当
当且仅当![]() ,即当
,即当![]() 依次成(递减)等差数列时,上式取“=”号。
依次成(递减)等差数列时,上式取“=”号。
![]() ,而且
,而且![]() ,故存在正整数
,故存在正整数![]() ,使原不等式恒成立。
,使原不等式恒成立。
评注:这道探索问题较难求解,但适当拆分因式,用基本不等式求解,不但解法新颖,而且过程也简捷。
例6 过曲线![]() 的直线
的直线![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 。(1)用
。(1)用![]() ;(2)证明
;(2)证明![]() ;(3)若
;(3)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
解:(1)点![]() ,直线
,直线![]() 方程为
方程为![]() ,令
,令![]() 可解得
可解得![]()
(2)由![]()
欲证![]() ,只需证
,只需证![]() ,即
,即![]() ,只需证
,只需证![]() 。可用数学归纳法证明
。可用数学归纳法证明![]() 。
。
(3)![]()

要使![]() 恒成立,只需
恒成立,只需![]() 。
。
![]()
评注:这是一道不等式、数列、函数的综合问题,它以二次曲线为背景,以直线方程为基础,建立数列![]() 的递推关系式,进而证明不等式,并通过证明数列
的递推关系式,进而证明不等式,并通过证明数列![]() 是递减数列完成解不等式。
是递减数列完成解不等式。
诊断检测
(一)选择题
1. 若![]() ( )
( )
![]()
2. 已知![]() 中最大的为( )
中最大的为( )
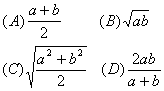
3. 设![]() ,则下列各式中正确的是( )
,则下列各式中正确的是( )
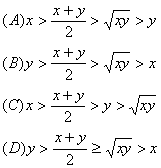
4. 与不等式![]() 解集相同的不等式( )
解集相同的不等式( )
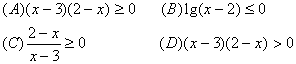
5. 已知![]() 都是不等于1的正数,则
都是不等于1的正数,则![]() 的最小值是( )
的最小值是( )
(A)3 (B)-3 (C)0 (D)不存在
(二)填空题
6. 设![]() 从小到大排列是_______________。
从小到大排列是_______________。
7. 使不等式![]() 都成立的
都成立的![]() 的关系式为________________。
的关系式为________________。
8. 不等式![]() 的解集为___________。
的解集为___________。
9. 不等式![]() 的解集为______________。
的解集为______________。
10. 若函数![]() 能取得负值,则实数
能取得负值,则实数![]() 的取值范围是____________。
的取值范围是____________。
(三)解答题
11. 已知![]() 。
。
12. 定义在(-2,2)上的奇函数![]() 是减函数,且
是减函数,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
13. 已知![]() 的最小值。
的最小值。
14. 设![]() 的最值。
的最值。
答案与提示:(一)1. D 2. C 3. A 4. B 5. D
(二)6. ![]() 7.
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]()
(三)11. 略证:(逆向运用公式)由![]() ,三式相加并注意
,三式相加并注意![]() ,则
,则![]() 。
。
12. 略解:首先考虑定义域有:

![]() ,因为
,因为![]() 上为减函数,所以
上为减函数,所以![]() 。
。
取两个范围的交集得![]() 。
。
注意:求解不等式问题切勿忽视函数的定义域。
13. 略解:![]() ,当且仅当
,当且仅当![]() 即
即![]() 时等号成立,所以
时等号成立,所以![]() 的最小值为9。
的最小值为9。
注意:若另解为:![]() ,
,![]()
![]() 最小值为8。这种解法是错误的,因为两次运用均值不等式,但取等号条件分别为
最小值为8。这种解法是错误的,因为两次运用均值不等式,但取等号条件分别为![]() 和
和![]() ,而这两式不能同时成立。
,而这两式不能同时成立。
14. 略解:设![]() ,即
,即![]() ,比较此式两边
,比较此式两边![]() 的系数,得
的系数,得![]() ,依题意,得
,依题意,得![]() ,
,
![]() 的最小值是5,最大值是10。
的最小值是5,最大值是10。
注意:有时变形是不可逆的,本题忽视这一点,易出错。
思想与方法
结合下面实例,挖掘解决不等式问题的思路与方法。
例7 (1985年上海市高考题)对于一切大于1的自然数![]() ,证明:
,证明:![]() 。
。
证法1:(1)当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,
,![]() 左边>右边,不等式成立。
左边>右边,不等式成立。
(2)假设![]() 时不等式成立,即
时不等式成立,即![]() ,两边乘以
,两边乘以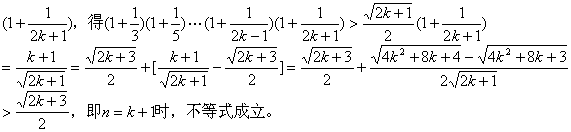 根据(1)、(2)对于大于1的自然数
根据(1)、(2)对于大于1的自然数![]() ,原不等式成立。
,原不等式成立。
证法2:设![]()
![]()
![]()
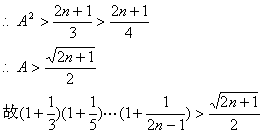
说明:证明不等式,常用的方法有比较法、综合法、分析法、数学归纳法和反证法。本题注意了根据欲证不等式的特点灵活选择,并恰当地“放缩代换”,这是证不等式不可忽视的两点。
例8 解不等式![]()
解法1:(转化为等价不等式组)原式等价于
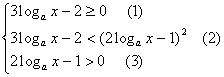
解(1)得![]() ,
,
![]() 解集为
解集为![]() 时,解集为
时,解集为![]() 。
。
解法2:(整体换元)令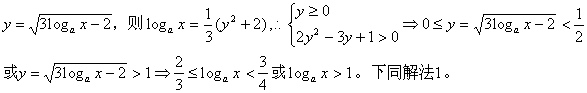 解法3:(通过局部换元后,用数形结合或讨论法求解)
解法3:(通过局部换元后,用数形结合或讨论法求解)
令![]()
![]() ,
,![]() ,由图像观察可得:
,由图像观察可得:![]()
说明:熟练掌握代数(有理、无理)及超越(指数、对数、三角)不等式的解法是高考中档试题的一个较为稳定的命题重点和热点,化高次为低次,化无理为有理,化多元为一元,化超越为代数,以及等价转化,分类讨论,数形结合,换元法等数学思想方法在本题多种解法中均有体现。
例9 二次函数![]() 的系数都是整数且
的系数都是整数且![]() ,在(0,1)内有两个不等的根,求最小的正整数
,在(0,1)内有两个不等的根,求最小的正整数![]() 。
。
解:令![]() 的两根为
的两根为![]() ,且
,且![]() ,于是
,于是![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]() 。
。
同理![]() ,且等号不同时成立,所以
,且等号不同时成立,所以![]() ,
,![]() ,而
,而![]() ,所以
,所以![]() ,故最小的正整数
,故最小的正整数![]() 。
。
说明:实系数一元一次、一元二次方程的实根与系数的关系,构成了高考重点、难点、热点问题,这类问题的解决要运用实系数方程实根分布的理论,这也是中学数学的一个重要内容,它体现了函数与方程的思想及数形结合的方法,不等式与方程互化的思想,本题正是运用了这些思想方法,才使问题化繁为简,顺利获解。
例10 设![]() ,
,![]() ,
,![]() 为常数,
为常数,![]() ,试求
,试求![]() 的最小值。
的最小值。
解法1:显然![]() ,于是有
,于是有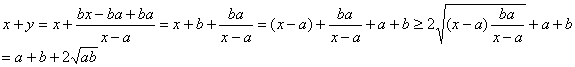 当
当![]() 时,
时,![]() 的最小值为
的最小值为![]() 。
。
解法2:本题也可用判别式法。
令![]() ,
,
![]() ,
,![]() 有最小值
有最小值![]() 。
。
解法3:用三角换元法
设![]() ,则
,则
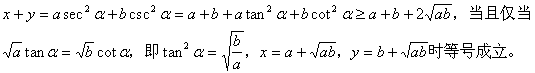
说明:最值问题也构成不等式在高考中的重点、难点、热点问题,掌握和运用两个和三个正数的算术平均数不小于它们的几何平均数定理是解决这类问题必不可少的基本技能与技巧。
强化训练
(一)选择题
1. 已知![]() 则( )
则( )
![]()
2. 若![]() 的最大值为( )
的最大值为( )
![]()
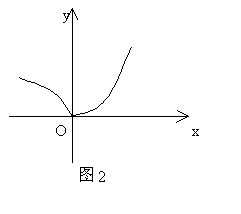
3. 已知函数![]() 的图像如图2,当
的图像如图2,当![]() 时,有
时,有![]() ,那么正确的结论是( )
,那么正确的结论是( )
4. 不等式![]() 的解集是( )
的解集是( )
![]()
5. 不等式组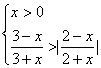 的解集是( )
的解集是( )
![]()
6. 不等式![]() 的解集是( )
的解集是( )
![]()
7. 母线长为1的圆锥体积最大时,其侧面展开图圆心角![]() 等于( )
等于( )
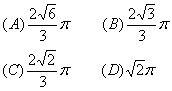
(二)填空题
8. 给出下列四个命题:(1)若![]() ;(3)若
;(3)若![]() ,则
,则![]() ;(4)若
;(4)若![]() ,其中真命题的序号是__________。
,其中真命题的序号是__________。
9. ![]() ,则
,则![]() 的大小关系为___________。
的大小关系为___________。
10. 若![]() ,使不等式
,使不等式![]() 在R上不是空集的
在R上不是空集的![]() 的取值范围是__________。
的取值范围是__________。
11. 不等式![]() 的解集是___________。
的解集是___________。
12. 设一长方体的体积为![]() ,则它的表面积的最小值为____________。
,则它的表面积的最小值为____________。
13. 若点![]() 在直线
在直线![]() 图像上(其中
图像上(其中![]() 为直角三角形三边长,
为直角三角形三边长,![]() 为斜边),则
为斜边),则![]() 的最小值为_____________。
的最小值为_____________。
14. 已知三个不等式:(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]() 。以其中两个作为条件,余下的一个作为结论,则可组成_______个正确的命题。
。以其中两个作为条件,余下的一个作为结论,则可组成_______个正确的命题。
(三)解答题
15. 设![]() ,解关于
,解关于![]() 的不等式,
的不等式,![]()
16. 给出函数![]() ,对任意
,对任意![]() ,且
,且![]() ,试比较
,试比较![]() 的大小关系。
的大小关系。
17. 若![]() 。
。
18. 在某两个正数![]() 之间,若插入一个数
之间,若插入一个数![]() ,使
,使![]() 成等差数列;若插入两个数
成等差数列;若插入两个数![]() 成等比数列,求证:
成等比数列,求证:![]() 。
。
19. 某工厂用平炉(主要使用焦炭,同时也用电)或电炉冶炼合金钢,用平炉冶炼每吨钢的费用为S元,用电炉冶炼每吨钢的费用为P元,若每吨焦炭为![]() 元,工业用电每百度为
元,工业用电每百度为![]() 元,则
元,则![]() 的关系为:
的关系为:![]() ,如果平炉比电炉炼一吨的费用低或相同,则用平炉生产,否则用电炉生产。
,如果平炉比电炉炼一吨的费用低或相同,则用平炉生产,否则用电炉生产。
(1)如果平炉与电炉冶炼费用相同,试将每吨焦炭价格表示为百度电费价的函数;
(2)如果每百度工业用电的价格在60元以上,用平炉生产,那么每吨焦炭的最高限价是多少元?
20. 是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。
答案与提示:1. A 2. C 3. D 4. A 5. C 6. C 7. A
8. (1)(2)(3) 9. ![]() 10.
10. ![]() 11.
11. ![]()
12. ![]() 13. 4 14. 3
13. 4 14. 3
15. 解:原不等式等价于不等式组
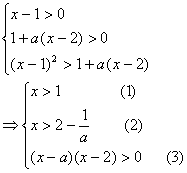
当![]() 且
且![]() 。
。
当![]() 。
。
当![]() ,故此时不等式组的解为
,故此时不等式组的解为![]() 。
。
16. 解:![]()
![]()
![]()
![]()
故![]()
17. 证明:要证![]() ,就是要证
,就是要证![]() ,即要证
,即要证![]() ,即证
,即证![]()
![]() ,
,![]() 成立。
成立。
![]() 成立。
成立。
18. 解:由题意可知: 用
用![]() ,应用均值不等式,得
,应用均值不等式,得
![]()
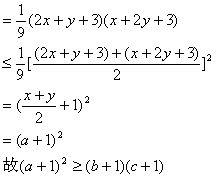
19. 解:本题是采用两种方式冶炼合金钢问题。
(1)由题意S=P,得![]() ;
;
(2)用平炉生产时,![]() ,即
,即![]() ,
,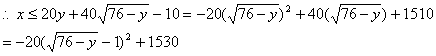

故若每百度工业用电的价格在60元以上,用平炉生产时每吨焦炭的最高价是1530元。
20. 略解:假设存在实数![]() ,使题中的不等式恒成立,即使
,使题中的不等式恒成立,即使![]() (1)恒成立。
(1)恒成立。
令![]() 取得最小值2,故要证(1)恒成立,需且只需
取得最小值2,故要证(1)恒成立,需且只需![]()
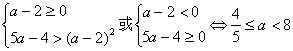 。
。
复习建议
1. 利用函数思想处理不等式有关问题
利用函数思想处理不等式问题,不但能提供有效的思路方法,而且对于提高知识的迁移能力,培养创造性思维也是大有裨益的。如:利用二次函数的图像讨论实系数一元二次方程根的分布问题,解(或证明)不等式问题。
例11 当![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
简析:对于这个含参数的不等式,若将不等式分离成含参数与不含参数两部分,把不含参数的部分视为一个函数,利用其最值处理,参数的取值范围将能快捷求出。
解:由![]()
![]()
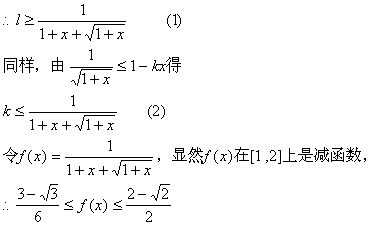
要使原不等式在[1,2]上恒能成立,即不等式(1)、(2)在[1,2]上恒成立,只需![]() 。
。
例12 正数![]() 。
。
分析:容易看出![]() 互为倒数,右式的
互为倒数,右式的![]() 暗示我们不能用均值不等式来证明,但正数“
暗示我们不能用均值不等式来证明,但正数“![]() ”,
”,![]() 又暗示我们可能要用到均值不等式,此时若能利用函数思想来处理,将会得到简捷的证明。
又暗示我们可能要用到均值不等式,此时若能利用函数思想来处理,将会得到简捷的证明。
事实上,由于函数![]() 上是增函数,且
上是增函数,且![]() 。
。
证明:(略)
总之,复习中应重视利用函数思想处理不等式有关问题,以培养和提高自身的数学素质。
2. 重视不等式的应用
不等式在方程、函数、参数及最值(值域或范围)中的广泛应用,几乎渗透到高中数学的各个章节,在解应用题中应用也十分广泛,近年来高考试题中的不等式的分数比重居高不下,特别是均值不等式的应用出现的频率很高,因而复习中应特别注意。
例13 (2000年全国新教材高考题)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求它的最大容积。
分析:本题的原解法是用导数知识实施的,但据题意及列式特点,配凑“和”为定值,借用均值不等式仍可获简解。
解:设容器的底面短边长为![]() ,则长边长为
,则长边长为![]() ,其高为
,其高为
![]() 。
。
于是,长方体的容积为:
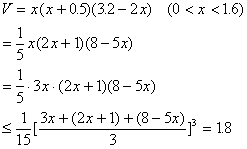
当且仅当![]() ,故所制作的容器的高是1.2m时,其容积取得最大值
,故所制作的容器的高是1.2m时,其容积取得最大值![]() 。
。
例14 某机关在“精减人员”中,对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的![]() 领取工资。该机关根据分流人员的特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,没有利润,第二年每人可获b元收入,从第三年起每人每年的收入可在上一年基础上递增50%。如果某人分流前工资收入每年
领取工资。该机关根据分流人员的特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,没有利润,第二年每人可获b元收入,从第三年起每人每年的收入可在上一年基础上递增50%。如果某人分流前工资收入每年![]() 元,分流后第
元,分流后第![]() 年总收入为
年总收入为![]() 元。
元。
(1)求![]() ;(2)当
;(2)当![]() 时,这个人哪一年收入最少,最少收入是多少;(3)当
时,这个人哪一年收入最少,最少收入是多少;(3)当![]() 时,是否一定可以保证这个人分流后的年收入永远超过分流前的年收入。
时,是否一定可以保证这个人分流后的年收入永远超过分流前的年收入。
解:(1)由题意知![]() 。
。
所以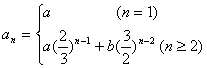
(2)![]()
![]()
![]() 。
。
要使上式等号成立,当且仅当![]() 。
。
解得![]() 元。
元。
(3)当![]()
![]() 。
。
上述等号成立,须![]() ,且
,且![]() 。
。
因![]() 不是自然数,因此等号不可能取到。所以当
不是自然数,因此等号不可能取到。所以当![]() 时,有
时,有![]() ,但当
,但当![]() 时,一定可以保证这个人分流一年后的年收入永远超过分流前的年收入。
时,一定可以保证这个人分流一年后的年收入永远超过分流前的年收入。
其它复习建议已渗透于以上各部分内容中,这里不再赘述。