高三数学第八章能力训练

 (一)选择题

1.给出下列命题：

①底面是正多边形的棱锥是正棱锥；

②侧棱都相等的棱锥是正棱锥；

③侧棱和底面成等角的棱锥是正棱锥；

④侧面和底面所成二面角都相等的棱锥是正棱锥，其中正确命题的个数是(　　)

A.0　　　　  B.1　　　　   C.2　　　　  D.3

2.两球体积和是12π，且两球大圆周长的和是6π，则这两个球半径的差是(　　)

A.3　　　　  B.2　　　　  C.1　　　　  D.0.5

3.地球表面北纬60°圈上有A、B两点，它们的经度差为180°，A、B两点沿纬度圈的距离与 地球表面A、B两点最短距离的比是(　　)

A.3：2　　　　  B.2：3　　　　  C.3：4　　　　  D.4：3

4.如图，已知圆台的轴截面ABCD，∠ABC＝60°，AB＝12，CD＝6 ，点E是下底面圆O上的一点，∠ABE＝30°，则DE与CO所成角α的正切的值等于(　 )

A.　　　　  B.　　　　  C.　　　　  D.

5.球O的半径R，A、B、C为球面上三点，A与B、A与C的球面距离为，B与C的球面距离为R，则球O在二面角B-OA-C内的 部分的体积是(　  )

A.πR³　　　　　　　　　  B.πR³

C.πR³　　　　　　　　　  D.πR³

6.三棱锥A-BCD的高AH=3a，且H是底面△BCD的垂心，若AB=AC，二面角A-B C-D为60°，G为△ABC的重心，则HG的长为(　　)

A.a　　B.a　　C. a　　D. a

7.底面半径为R，高为H的圆锥的内接正方体的棱长为(　　)

A.　　　　　 B.　　　 C.　　　 D.

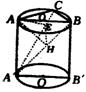
8.如下图，已知AA′B′B是圆柱的轴截面，C是底面圆周上一点，且 ∠CAB＝α，∠CA′B＝β，∠ABA′＝θ，则α、β、θ三个角之间的关第是(　　)

A.sinαcosθ=sinβ　　　　　　  B.cosαcosθ=cosβ

C.sinα=sinβcosθ　　　　　　  D.cosα=cosβcosθ

9.用一张半径为R的圆形滤纸，做一个容量最大的过滤器(圆锥体)，则将这个圆形滤纸剪去 一个扇形的中心角θ(弧度)应是(　　)

A.2π-π　　　　  B.2π-π　　　　  C.　　　　  D.

10.正四棱台ABCD-A₁B₁C₁D₁的上底边长：侧棱长：下底边长＝1∶2∶3，则其面对 角线AD₁与B₁C所成角的余弦值为(　　)

A.　　  B.　　　 C.-　　  D.

(二)填空题

11.圆锥的侧面展开图是一个半圆，有一个半球的底面恰好为该圆锥的底面，半球面将圆锥 侧面分成上、下两部分，这两部分面积分别是S₁、S₂，则S₁∶S₂＝　　　　　　 .

12.把一个大金属球 表面涂漆，需油漆2.4kg，若把这个金属球熔化， 制成 64个半径相等的小金属球(设损耗为零)，将这些小金属球表面涂漆，需用油漆　　　　　  .

13.如图，一块铁皮呈等腰梯形状，两底分别为4a，2a，高SC 为a，S是AA′的中点，将梯 形沿虚线折成一个四棱锥S-ABCD的侧面(如图)(A重合于A′)，该四棱锥的体积为　　　　  .

14.正四棱台ABCD-A₁B₁C₁D₁，上底AB=1，下底A₁B₁=2，侧棱AA₁与底面成60 °角，则侧面梯形ABB₁A₁的对角线BA₁与下底面所成的角为　　　　 .

15.如图，在正三角形ABC中，E、F分别是AB、AC的中点，AD⊥BC，EH⊥BC，FG⊥BC，D 、H、G为垂足，若将正△ABC绕AD旋转一周所得圆锥的体积记为V，则其中由阴影部分所产生 的旋转体的体积与V的比值是　　　 　 .

(三)解答题

16.设圆台的高为h，母线与下底所成的角为α，轴截面中一条对角线垂直于腰，求圆台的 侧面积.

17.已知球的外切圆台的体积是球体积的倍，求这个圆台的母线与底 面成角的大小.

18.求半径为R的球内接圆锥侧面积的最大值.

19.如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AB＝5cm， AD＝8cm，∠BAD＝60°，PA＝cm，且PA⊥平面ABCD，点E在PA上，且 PC∥平面BED.

①求这个四棱锥被截面BED分成两部分的体积；

②求顶点A到截面BED的距离。

20.如图，斜三棱柱ABC-A₁B₁C₁的底面是Rt△ABC，∠A＝90 °，且BC₁⊥AC，作C₁ H⊥底面ABC，垂足为H。①试判断H点的位置，并说明理由。②若AB＝AC＝2，AC₁＝2，侧棱与底面成60°角，求三棱柱ABC-A₁B₁C₁的体积.

21.已知AA′B′B是圆柱的轴截面，C是上底面圆周上不同于A，B的一点.①求证平面BA′ C⊥平面AA′C；②当棱锥A′-ABC的体积V′和圆柱的体积V的比是1：2，求 二面角B-AA′-C的大小；③设A-A′B-C为α，又∠CAB=β，∠CA′B=γ，求证sinα=.

参考答案：

(一)　1.A  2.C　3.A　4.C  5.C　6.B　7.C  8.A

9.B  10.D

提示：

5.可求得二面角B-OA-C的平面角就是∠BOC=60°，因此两个半圆面所夹的体积是球体积的.

 (二)11.1∶3　12.9.6kg　13. a³　14 .arctg　 15.5∶8

(三)16.设圆台的截面A₁ABB₁，上、下底半径分别为r和R， 母线长为l，A₁D⊥AB于

D，则A₁D＝h，∠A₁AB＝α，则BD＝h·tgα，而BD＝R+r，即BD＝R+r＝h·tgα，t=h· cscα.

S_侧＝π(R+r)l=πh²secα.

17.画出轴截面图，设圆柱上、下底半径分别为a、b，可依题设条件求得内切球半径R=，由得=，化简得b=2a，易知母线与底面所成角θ的正切值tgθ==2，因此母线与底面所成角为arctg2.

18.设圆锥顶角为2α，则母线l=2Rcosα，底面圆半径r=Rsinα，则 圆锥侧面积.

S=πγl= 2πR²sin2αcosα= 4πR²sinαcos²α

其中令y=sinαcos²α，则

y²=sin²αcos⁴α=sin²α(1-sin² α)²

=·2sin²α·(1-sin²α)(1-sin²α)

≤〔〕³=

当2sin²α=1-sin²α即sinα=时，等号成立，

∴y≤　∴S≤πR²

即圆锥侧面积的最大值是πR².

19.①如图，AB∩BD＝O，则OE是平面BED和平面APC的交线，由PC∥ OE　E是PA中点，从而EA＝。易知

V_E-ABD＝，V_EPBCD＝V_P-ABD＝ (cm³).

②作AF⊥BD，垂足为F，连EF，易证平面EAF⊥平面BED，作AH⊥AEF中，AE＝cm，AF＝cm，EF＝cm，可知∠FEA＝60°，因此AH＝AE。sin60°＝(cm)，即为所求A到平面BED的距离.

20.①C₁H⊥平面ABC，连结BH，则BH是BC₁是在平面ABC的射影。

BC₁⊥AC，BH⊥AC，又BA⊥AC，而在平面ABC内，过B只有一条直线垂直于AC，故BA，BH重 合，故H点在BA直线上。

②连结CH，则∠C₁CH＝60°，设C₁H＝x，则CH＝x，在Rt△CAH中，AH₁＝(x)²-2²，在Rt△C₁ HA中，AH₁＝(2)²-x²，x²-4＝28-x²，x ²＝24，x＝2，又S_△ABC＝×2×2＝2，V_棱柱＝2·2＝4。

21.①略.　②易知∠BAC是二面角B-AA′-C的平面角，设圆柱底半径为r，高为h，∠CAB=β，则V_{A ′-ABC}=·S_△ABC·h=··2sinβ·2rcosβ·h=r²s in²β又圆柱体积V=πr²h，由V_A′-ABC：V=1:2，得sin2β=，2β=60°或120°，故二面角B-AA′-C，为60°或30°.

③由①得平面BA′⊥平面AA′C，作AE⊥A′C，则AE⊥平面BA′C，作EH⊥A′B，连结AH，可 知∠AHE是二面角A-A′B-C的平面角，∠AHE=α，sinα=，其中AE= AC·cos∠AA′C=2rcosβ·；AH=AB·cos∠AA′B=2r·，∴，即sinα=.