西安中学高三年级第一学期期中考试

数学试题

一、选择题（本大题共有12小题，每小题5分，共60分）

1．已知M={xy=x，x∈R}，，则M∩N等于（　 ）

A．{（0，0），（1，1）}　　　　　 B．{ xx∈R }

C．{yy≥0}　　　　　　　　　　  D．φ

2．已知集合A={a，b，c}，集合B={m，n}，设映射f：A→B。如果集合B中的元素都是A中元素在f下的象，那么这样的映射f有（　　）

A．8个　 　　 B．6个　　　 C．4个　　　 D．2个

3．奇函数y=f(x)（x∈R）有反函数，则必在的图象上的点是（　　）

A．（-f(a)，-a）　　　　 B．

C．（-f(a)，a ）　　　　 D．

4．已知f(x)是定义在R上的奇函数，当x<0时，，那么的值是（　　）

A．　　　　 B．　　　　C．　　　　D．9

5．函数的单调递减区间是（　　 ）

A．　　　　　 B．

C．　　　　　  D．

6．定义在R上的函数f(x)、g(x)都是奇函数，函数F(x)=af(x)+bg(x)+3在区间（0，+∞）上的最大值为10，那么函数F(x)在（-∞，0）上的最小值为（　 ）

A．-10　　　 B．7　　　　C．-7　　　D．-4

7．若把函数y=f(x)的图象做平移，可以使图象的点P（1，0）变换成点Q（2，2），则函数y=f(x)的图象经过此变换后所得图象对应的函数为（ 　 ）

A．y=f(x-1)+2　　　　　　　 B．y=f(x-1)-2

C．y=f(x+1)+2　　　　　　　 D．y=f(x+1)-2

8．若直线a∥平面α，直线b∥平面α，那么a与b不可能（　　）

A．相交　　　　B．异面　　　 C．平行　　　D．垂直

9．圆台上、下底面面积分别为，平行于底面的截面面积为，那么截面到上、下底面距离之比为（　　）

A．2：1　　　　B．1：2　　　 C．3：1　　　 D．1：3

10．圆锥的高h=8，它的侧面展开图的圆心角是216°，那么这个圆锥的全面积是（　　）

A．96π　　B．24π　　  C．84π　　　D．60π

11．正四棱台下底面为ABCD，上底边长：侧棱长：下底边长=1：2：3，侧面对角线所成角的余弦值为（　　）

A．　　　 B．　　 C．　　  D．

12．三棱锥A-BCD的高，H为底面△BCD的垂心，若AB=AC，二面角A-BC-D等于60°，G为△ABC重心，则HG的长为（　　）

A．　　　　B．　　  C．　　　 D．

二、填空题（本大题共有4道小题，每小题4分，共16分）

13．若（x≤0），则=_______________。

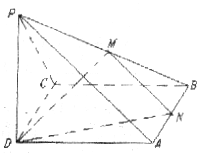
14．（如右图）矩形ABCD边长分别为15，20，PA⊥平面ABCD，则点P到CD边的距离为_______________；点P到BD的距离为_______________。

15．（理科做）球外切圆台的上、下底半径分别为1和3，则球的体积是_______________。

（文科做）二面角内有一点，它到两个面的距离相等，并且等于它到棱的距离的一半，这个二面角的度数为_______________。

16．若f(x)是定义在R上的奇函数，且f(x-2)=-f(x)，给出下列四个结论：

①f(2)=0；

②f(x)是以4为周期的函数；

③f(x)的图象关于直线x=0对称；

④f(x+2)=f(-x)。

其中所有正确结论的序号是_______________。

三、解答题（本大题共有6道小题，17-21题每小题12分，22题14分，共74分）

17．已知函数f(x)是奇函数，而且在（0，+∞）上是增函数，那么f(x)在（-∞，0）上是增函数还是减函数？写出你的推理过程。

18．如图，三棱锥P-ABC的底面△ABC内接于圆O，PA垂直于圆O所在的平面。

（1）求证：平面PAC⊥平面PBC。

（2）若PA：PB=4：3，，求直线PB和PAC所成角的大小。

19．已知关于x的方程lg(x-1)+lg(3-x)=lg(a-x)有实数解，求实数a的取值范围。

20．已知四棱锥P-ABCD的底面是边长为4的正方形，PD⊥底面ABCD，若PD=6，M，N分别是PB，AB的中点。

（1）求证：MN⊥CD；

（2）求三棱锥P-DMN的体积；

（3）求二面角M-DN-C的平面角。

（文科不做第（3）问）

21．有甲、乙两种商品，经营销售这两种商品所获的利润依次是P万元和Q万元，它们与投入资金x万元的关系可由经验公式给出：，今有3万元资金投入经营甲、乙两种商品，为获得最大利润，对甲、乙两种商品的资金投入分配应为多少才能获得最大利润？

22．（理科做）已知函数（0<a≠1，k∈R）。

（1）当0<a<1时，若f(x)在[1，+∞]内有意义，求k的取值范围；

（2）当a>1时，若f(x)的反函数就是它本身，求k的值；

（3）在（2）的条件下，解方程。

（文科做）设函数y=f(x)满足lg(lgy)=lg(3x)+lg(3-x)，

（1）求f(x)的表达式；

（2）求f(x)的值域；

（3）求f(x)的单调区间。

参考答案：

一、选择题（每小题5分，共60分）

1．C　2．B　3．A　4．C　5．D　6．D　7．A　8．C　9．A　10．A　11．D　12．B

二、填空题（每小题4分，共16分）

13．0

14．；15

15．；60°

16．①②④

三、解答题（共6道小题，17-21题每小题12分，22题14分，共74分）

17．解：设，则

∵f(x)在（0，+∞）上是增函数，

∴

又f(x)是奇函数，

∴

∴

故f(x)在（-∞，0）上是增函数

18．证（1）∵PA⊥平面ABC，

∴PA⊥BC

又∵AB是⊙O的直径

∴BC⊥AC

∴BC⊥平面PAC

又

∴平面PAC⊥平面PBC

（2）∵BC⊥平面PAC

∴∠BPC为PB和平面PAC所成的角

设PA=4k，AB=3k，则PB=5k

∵，

∴

在Rt△PCB中，

∴∠BPC=30°为所求

19．解：原方程等价于

由其图象易得当时，

原方程有解

20．（1）∵PD⊥平面ABCD

∴PD⊥CD

又CD⊥DA，

∴CD⊥平面PDA

∴CD⊥PA

又∵M、N分别是PB、AB的中点

∵MN∥PA

∴MN∥CD

（2）设AC∩BD=0，连MO、PN

∵MO∥PO

∴MO⊥平面ABCD且

∵N是AB的中点，

∴

∴

（3）过O作DN作垂线OK，垂足为K，连ON，MK

则MK⊥ND

∴∠MKO是二面角M-DN-C的平面角

∵

又

∴

∴

∴为所求。

21．解：设投入乙种商品的资金为x万元，则投入甲种商品的资金为（3-x）万元。

依题意，甲种商品可获利万元，乙种商品可获利万元，共获利为

当，即时

（万元）

答：甲种商品投入0.75万元，乙种商品投入2.25万元，可获得最大利润1.05万元。

22．（理科）解：f(x)在[1，+∞）内有意义，

即时x∈[1，+∞）均成立，

即时x ∈[1，+∞）均成立

∵0<a<1，∴

∴在[1，+∞）上是增函数，

当x=1时，其最小值为1，

∴当k<1时，f(x)在[1，+∞）内有意义

（2）显然k≠0，

从而

∴

为使对f(x)定义域内的一切x都成立，

则，

整理得对定义域中的一切x都成立

∴

此时（x<1）

（3）由a>1，及x<1得

∴原方程有唯一解x=-1

（文科）解：（1）（0<x<3）

（2）令，当x∈（0，3）时，

∴

（3）f(x)在上递增，在上递减。