综合练习 (五)

　　　　班级：______________，姓名：___________________, 成绩：________________

一. 选择题：(每小题4分，共4×10 = 40分)将正确答案填入下表中

1. 若集合A = {y y = x², xÎR}, B = {y y = x³, xÎR}，则AB =
　　　(A) R　　(B) [0, +¥)　　(C) { (1, 1) }　　(D) { (0, 0), (1, 1) }

2. 若函数f (x) = ()^1－x，则其反函数的图象是

　　

　　　  (A)　　　　　　　  (B)　　　　　　　　  (C)　　　　　　　 (D)

3. 已知复数z = 2 +i，把z对应的向量分别依顺时针和逆时针方向旋转，得到的向量分别对应复数z₁, z₂，那么z + z₁ + z₂等于
　　　(A) z　　(B)－z　　(C) 0　　(D) 2z

4. 使tgx < ctgx成立的 一个区间是
　　　(A) [, p)　　(B) (p,]　  (C) [－, 0)　  (D) [－,－]

5. (理)方程(r为参数，q为常数且 q <)所表示的曲线是
　　　(A)以点(0,－1)为圆心，r为半径的圆　　(B)以点(0,－1)为圆心，r为半径的一段圆弧

　　　(C)过点(0,－1)，倾斜角为q的直线　　　(D)过点(0,－1)，倾斜角为－q的直线

　 (文)圆x² + y² + 4x－2y－4 = 0上的点到点P(1, 5)的最近距离为
　　　(A) 3　　(B) 5　　(C) 1　　(D) 2

6. 一棱锥被平行于底面的平面截成一个小棱锥和一个棱台. 若小棱锥及棱台的体积分别为y和x，则y关于x的函数的图象的形状大致为

　　　　

　　　 (A)　　　　　　 (B)　　　　　　 (C)　　　　　　 (D)

7. 在轴截面为直角三角形的圆锥内有一个内接圆柱，若圆柱的全面积等于圆锥的侧面积，则圆柱的高与圆锥的高之比为
　　　(A)　　(B)　　(C)　　(D)－1

8. 已知数列{a_n}的前n项和S_n = 1－a_n，则S_n =
　　　(A) 1　　(B) 　　(C) 　　(D)

9. 若f (x)在集合D上有定义，且存在M > 0，使得对任意xÎD都有f (x) < M，称函数f (x)在D上是有界的. 则下列函数中无界的是
　　　(A) y = sinx + cosx　(B) y =　 (C) y =　(D) y =

10. 某金库设在一占地10000m²的正方形城堡内，周围每隔25m设立一个哨位. 现因人员紧张保卫部门在每个班次只能派出9人，为确保安全，城堡的每一面至少应有三个哨位有人值守，则不同的派驻方法(只考虑哨位，不考虑人员情况)共有
　　　(A) 216种　　(B) 432种　　(C) 324种　　(D) 648种

二. 填空题：(每小题4分，共4×4 = 16分)

11. 不等式－3 < 1的解集是______________________________ .

12. 以椭圆x² + 4y² = 4的长轴的一个顶点为直角顶点作一个内接于椭圆的等腰直角三角形，则该三角形的面积是______________ .

13. 正四棱锥S－ABCD，截面CEFG与SD, SA, SB分别相交于E, F, G，则当截面CEFG满足条件________________时，有GE^SC .

14. 三个数6、3、－1排成一排，在6与3之间插入二个实数a, b；在3和－1之间插入一个实数c，使6, a, b三个数成等差数列，3, c, －1三个数也成等差数列，且a, b, c三个数成等比数列，那么a, b, c这三个数的和可能是：①；②3；③；④7. 其中正确的序号是_______________ .

三. 解答题：(共44分)

15. 已知复数z满足z－3`z =－4 + 4i. (1)求复数z；(2)设a = argz，计算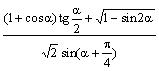的值.

16. 解关于x的不等式：log_a (x²－x－2) > log_a (x－) + 1 (a > 0且a¹1)

17. 已知AB是椭圆+= 1 (a > b > 0)的一条弦，M(2, 1)是弦AB的中点，以M为焦点，椭圆的右准线为相应准线的双曲线与直线AB交于N (4,－1). (1)设双曲线的离心率为e，试用椭圆的半长轴长表示e；(2)当椭圆的离心率是双曲线离心率的倒数时，求椭圆的方程；(3)求椭圆长轴长的取值范围.

18. 已知二次函数f (x) = ax² + bx + c (a, b, cÎR)满足f (1) = 1且f (－1) = 0，对于任意实数x都有f (x) > x. (1)证明：a > 0, c > 0；(2)设函数g (x) = f (x)－mx (xÎR)，求m的取值范围，使函数g (x)在区间[－1, 1]上是单调函数.

参考答案：

一．

1	2	3	4	5	6	7	8	9	10
B	A	C	B	D	B	B	A	D	D

二. 11. (6, 18); 12. 16/25; 13. CG = CE或SA^平面CEFG或SE = SG, ……; 14.①④;

三.　15. (1). z = 2 + i; (2)tga = 1/4, aÎ(0, p/4)，原式= 1/(1+tga) = 2/3;

16. 0<a<1时，解集为Æ；a > 1时，解集为{x x > a + 1};

17. (1) e = 2/a - 2Ö2; (2)x²/18 + y²/9 = 1; (3) (2Ö6, 4Ö2)È(4Ö2, 4+4Ö2);

18. (1)由f (1) = 1且f (-1) = 0∴a + c = b = 1/2∵对于任意实数x都有f (x) - x > 0∴1/4 - 4ac < 0且a > 0∴a > 0, c > 0; (2) ∵a + c > 2Ö(ac) ∴ac < 1/16，又ac > 1/16∴ac = 1/16∴a = c = 1/4∴f (x) = 1/4x² + 1/2x + 1/4, g (x) = 1/4[x² + (2 - 4m)x + 1]. 要使g (x)在[-1, 1]上单调，则(4m - 2)/2 > 1，解得m < 0或m > 1.