上海市南汇区2005学年度第一学期期未考试

高三数学试卷

（满分：150分，完卷时间：120分钟）

考生注意：本试卷为文、理合卷，题首标有“文”、“理”分别是文科生、理科生做的题目，没有标记的是共同做的题目。

题号	1-12	13-16	17	18	19	20	21	22	总分
得分

一、填空题：（本题满分48分，每小题4分）

1、已知集合A=,B=,则AB=。

2、若sin= -,则cos 2=。

3、方程的解是

4、已知函数f(x)的图象与函数的图象关于直线y=x对称，则f(9)=__2__。

5、复数的共轭复数＝

6、在数列中a= -13,且3a=3a -2,则当前n项和s取最小值时n的值是__20__。

7．集合，在A中任取一元素m和在B中任取一元素 n,则所取两数m>n的概率是_0.6_。

8、在△ABC中三边之比a:b:c=2:3:,则△ABC中最大角=。

9、（理）在的展开式中，的系数是和的系数的等差中项，若实数，那么.

（文）设实数x,y满足条件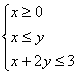则的最大值是_1_。

10、在棱长为4厘米的正方体ABCD-A₁B₁C₁D₁中，E，F分别是AB，BC的中点，那么点B到平面B₁EF的距离是厘米。

11、在R上定义运算△：x△y=x(1 -y) 若不等式(x-a)△(x+a)<1,对任意实数x恒成立，则实数a的取值范围是　　。

12、已知数列，，把数列

的各项排成三角形状，如图所示．记　

表示第m行，第n列的项，则

=

二、选择题：（本题满分16分，每小题4分）

13、设a,b,c表示三条直线，表示两个平面，下列命题中不正确的是（ D　）

(A)　　　(B)　

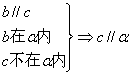(C)　　(D)　

14、函数y=cos 2x的图象的一个对称中心是（　B　 ）

(A )()　　 (B) ()　　(C )(-)　　(D) (0,0)

15、函数y=　 （　B　 ）

(A)在(-,+)上单调递增。　　

(B)在上是减函数，在上是增函数。

(C)在上是增函数，在上是减函数。

(D)在上是减函数，在上是增函数。

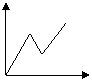
16、某人骑自行车沿直线匀速旅行，先前进了千米，休息了一段时间，又沿原路返回千米（，再前进千米，则此人离起点的距离与时间的关系示意图是（　C  ）

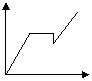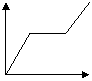　 （A）　　　　  （B）　　　　  （C）　　　　  （D）

三、解答题：

17、（12分）设为虚数，且满足2，求。

解：设，　　　  ______2分

则　　  _________6分

由已知得，∴=0　 　 ________8分

∴ 　　　________10分

∴=1　　　　　　 _______12分

18、（13分）已知向量，

定义函数f(x)=。（1）求函数f(x)的最小正周期。

（2）xR时求函数f(x)的最大值及此时的x值。

解：f(x)=-1=2sinx×cosx+2cosx-1

=sin2x+cos2x=2sin(2x+)　　　　 ——7分

（1）T==　　　 ——9分

（2）f(x)=2sin(2x+)

∴当2x+=+2k (kZ)

即x=+k (kZ)时，f(x)取最大值为2

∴当x=+k (kZ)时f(x)=2　　　——12分

19、（本题满分13分）（文）直三棱柱ABC-A₁B₁C₁的底面为等腰直角三角形，BAC=90⁰，AB=AC=2，AA=2，E_, F分别是BC、AA₁的中点。求（1）异面直线EF和A₁B所成的角。（2）直三棱柱ABC-A₁B₁C₁的体积。

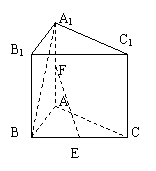解：（1）方法一：（略解）取AB的中点D，连DE、DF，

　　　　则∥，

∴∠DFE即为所求。——2分

由题意易知，，，

由DE⊥AB、DE⊥A A₁得DE⊥平面ABB₁A₁

∴△DEF为直角三角形，∠EDA=90⁰

∴tan∠DFE= ——9分

∴,即异面直线EF和A₁B所成的角为。——10分

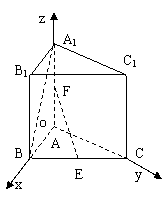方法二：

以A为坐标原点以AB、AC、

AA₁所在直线分别x轴、y轴、

Z轴建立如图所示的直角坐标系，

则A (o,o,2)　B (2,0,0)

E、F分别是BC、AA₁中点

∴E(1,1,0) F(0,0,)　 ——5分

∴

　 

设的夹角为∴cos=

　∴ 　　 ——9分

∴异面直线EF和AB所成的角为　　 ——10分

（2）直三棱柱ABC-A₁B₁C₁的体积 ——13分

（理）如图，直四棱柱中，底面是直角梯形，，，异面直线与互相垂直。（1）求直棱柱棱的长；（2）若点在线段上，，求直线与平面所成的角的大小。

解：（1）方法1:

以A为坐标原点以AB、AD、

AA₁所在直线分别x轴、y轴、

Z轴建立直角坐标系，

设棱的长为

则A (0,0,0)，B (5,0,0)，

C(5,2,0),D(0,8,0),

A₁(0,0,a), B₁(5,0,a), C₁(5,2,a),D₁(0,8,a).

∴，——3分

又， ——6分

得，∴棱的长为4。——8分

方法2 、设棱的长为在A₁D₁ 上取点E₁，使A₁E₁=2，则点E₁即为点C₁在平面AA₁D₁D上的射影，AE₁⊥A₁D。连C₁E、AE₁,易知A₁D⊥平面AC₁E₁，

在平面AA₁D₁D中，由Rt△AA₁D～Rt△AA₁E

∴，即。∴∴棱的长为4。——8分

（2）由（1）知，M点即为AE₁与A₁D的交点，由题意显然∠MAD即为所求。——10分

又∠MAD=∠AE₁A₁

∴　——12分

∴直线与平面所成的角的大小是。——13分

20、（本题满分14分）某自来水厂的蓄水池存有400吨水，水厂每小时可向蓄水池中注水60吨，同时蓄水池又向居民小区不间断供水，小时内供水总量为吨，（）

（1）从供水开始到第几小时时，蓄水池中的存水量最少？最少水量是多少吨?　　　

（2）若蓄水池中水量少于80吨时，就会出现供水紧张现象，请问：在一天的24小时内，有几小时出现供水紧张现象。

解：（1）设小时后蓄水池中的水量为吨，

则； ——3分

令＝；则，即；——5分

∴当，即时，，

即从供水开始到第6小时时，蓄水池水量最少，只有40吨。—8分

（2）依题意，得 ——11分

解得，，即，；

即由，所以每天约有8小时供水紧张。——14分

21、（本题满分16分）已知数列的前n项和S=50n-n(n)

（1）求证是等差数列。

（2）设b=,求数列的前n项和T_n

（3）求()的值

解：（1） ，因此，当时有

 

所以　 ………………3分

　　　　 ∴，

故是首项为49，公差为的等差数列…………6分

（2）若，则　……………7分

设，当时，则，

此时，；　　……………………9分

当时，，

而

所以 　 

　　 综合所得 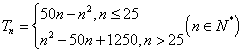 ………14分

　  （3）lim()=()= -1　…………16分

22、(本题满18分)

设函数f(x)=ax+bx+1（a,b为实数）,F(x)=

（1）若f(-1)=0且对任意实数x均有f(x)成立，求F(x)表达式。（2）在（1）的条件下,当x时,g(x)=f(x) -kx是单调函数，

求实数k的取值范围。

（理）（3）设m>0,n<0且m+n>0,a>0且f(x)为偶函数，求证：F(m)+F(n)>0。

解：（1）f(-1)=0

　　　 ∴由f(x)0恒成立 知

△=b-4a=(a+1)-4a=(a-1)0 ——（理）2分----(文)3分

∴a=1从而f(x)=x+2x+1　　 ——（理）4分----(文)6分

∴F(x)= —（理）6分-----(文)9分

（2）由（1）可知f(x)=x+2x+1

 ∴g(x)=f(x)-kx=x+(2-k)x+1—（理）8分-----(文)12分

由于g(x)在上是单调函数,知

-或- ——（理）10分---(文)16分

得k-2或k6 ——（理）12分-----(文)18分

（3）f(x)是偶函数

∴f(x)=f(x)而a>0∴在上为增函数

对于F(x)

当x>0时-x<0

F(-x)=-f(-x)=-f(x)=-F(x)　　——（理）14分

当x<0时-x>0

　　　  F(-x)=f(-x)=f(x)=-F(x)

∴F(x)是奇函数且F(x)在上为增函数—（理）16分

m>0,n<0由m>-n>0知F(m)>F(-n)

∴F(m)>-F(n)

∴F(m)+F(n)>0　　　　 ——（理）18分