高中数学必修1复习卷( C)

　　　　　　　  考号　　 班级　　　 姓名　　　　　 

一、选择题

（1）若集合A={1，3，x}，B={1，}，A∪B={1，3，x}，则满足条件的实数x的个数有（　 ）

（A）　1个　（B） 2个　 （C）3个　（D）　4个

（2）集合M={（x，y） x＞0，y＞0}，N={（x，y） x+y＞0，xy＞0}则（　）

（A）M=N　 （B）M  N　　 （C）M  N　 （D）MN=

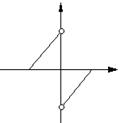
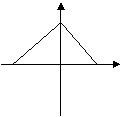（3）下列图象中不能表示函数的图象的是　（　）

　　  y　　　　　　　　　　　　　　　　 y　　　　　　　　　  y　

　　　o　　　x　　x　 o　　 x　　　 o　　 x　　　　

（A）　　　　　　　　 （B）　　　　（C）　　　　　　  (D)

（4）若函数y=f（x）的定义域是[2，4]，则y=f（）的定义域是（　 ）

（A） [，1]　（B） [4，16]　（C）[，]　（D）[2，4 ]

（5）函数的定义域为（　 ）

（A） （B）（-2，+∞） （C） （D）

（6）设偶函数f（x）的定义域为R，当时f（x）是增函数，则的大小关系是（　）

（A）＞＞　（B）＞＞

（C）＜＜　（D）＜＜

（7），，，那么（　　 ）

（A）a＜b＜c　　（B）a＜c＜b　（C）b＜a＜c　（D）c＜a＜b

（8）已知函数，其中nN，则f（8）=（　）　 C

（A）6　　（B）7　 （C）　2　　（D）4

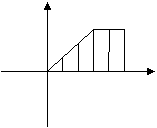
（9）某工厂今年前五个月每月生产某种产品的数量C（件）关于时间

t（月）的函数图象如图所示，则这个工厂对这种产品来说（　）　　　　　　 O　一二 三 四五 t

（A）一至三月每月生产数量逐月增加，四、五两月每月生产数量逐月减少

（B）一至三月每月生产数量逐月增加，四、五月每月生产数量与三月持平

（C）一至三月每月生产数量逐月增加，四、五两月均停止生产　　　　　　　　

（D）一至三月每月生产数量不变，四、五两月均停止生产

（10）若函数f（x）和g（x）都为奇函数，函数F（x）=af（x）+bg（x）+3在（0，+∞）上有最大值10，则F（x）在（-∞，0）上有（　　）

（A）　　  最小值 -10　（B）最小值 -7　（C）最小值 -4 （D）最大值 -10

（11）若函数的定义域和值域都是[0，1]，则a=（　）

 （A）　　 （B）　（C）　　 （D）2

（12）如果二次函数f（x）=3x²+bx+1在（-∞，上是减函数，在，+∞）上是增函数，则f（x）的最小值为（　 ）

（A）　 （B）　 （C）　　  （D）

二、填空题

（13）函数的定义域为　　　　　　 　　  .

（14）若集合M={x x²+x-6=0}，N={x kx+1=0}，且NM，则k的可能值组成的集合为　　　　　　   .

（15）设函数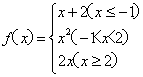　，若f（x）=3，则x= 　　　　 .

（16）有以下4个命题：

　　①函数f（x）= a^x（a＞0且a≠1）与函数g（x）=log _aa^x（a＞0且a≠1）的定义域相同；

②函数f（x）=x³与函数g（x）=3 ^x的值域相同；

③函数f（x）=（x-1）²与g（x）=2 ^{x -1}在（0，+∞）上都是增函数；

④如果函数f（x）有反函数f ^-1（x），则f（x+1）的反函数是f ^-1（x+1）.

其中的题号为　　　　　　   .

三、解答题

（17）计算下列各式

（Ⅰ）　（Ⅱ）  

（18）定义在实数R上的函数y= f（x）是偶函数，当x≥0时，.

（Ⅰ）求f（x）在R上的表达式；

（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）.

（19）已知二次函数f（x）图象过点（0，3），它的图象的对称轴为x = 2，

且f（x）的两个零点的平方和为10，求f（x）的解析式.

（20） 已知函数 ，（x∈（- 1，1）.

（Ⅰ）判断f（x）的奇偶性，并证明；

（Ⅱ）判断f（x）在（- 1，1）上的单调性，并证明.

（21）　商场销售某一品牌的羊毛衫，购买人数是羊毛衫标价的一次函数，标价越高，购买人数越少。把购买人数为零时的最低标价称为无效价格，已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件，商场以高于成本价的相同价格（标价）出售. 问：

（Ⅰ）商场要获取最大利润，羊毛衫的标价应定为每件多少元？

（Ⅱ）通常情况下，获取最大利润只是一种“理想结果”，如果商场要获得最大利润的75%，那么羊毛衫的标价为每件多少元？

2009届六安二中高三必修1复习卷( C)

一、选择题　 CADCC　　ACBBC　　AD

二、填空题

 （13） （0，1）　　　　　  （14）{0，，}

 （15）　　　　　　　　　（16） ②③④

三、解答题

（17）解：（Ⅰ）原式=lg²2+（1- lg2）（1+lg2）—1

　　　　　　　　　 =lg²2+1- lg²2- 1=0　　　　　　　　

（Ⅱ）原式=

　　　　  =2²×3³+2 — 7— 2— 1 =100　　　　　　　

（18）解：（Ⅰ）设x＜0，则- x＞0， 　∵f（x）是偶函数，

∴f（-x）=f（x） ∴x＜0时，

　 所以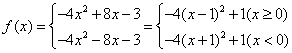　

（Ⅱ）y=f（x）开口向下，所以y=f（x）有最大值f（1）=f（-1）=1

　　 函数y=f（x）的单调递增区间是（-∞，-1和[0，1]

　　　　　　　　　 单调递减区间是 [-1，0]和[1，+∞　

（19）解：设f（x）= ax²+bx+c （a≠0）

　　 因为f（x）图象过点（0，3），所以c =3　　　　　　

　　 又f（x）对称轴为x=2，  ∴　=2即b= - 4a

所以　　　　　　　　　　

设方程的两个实根为 x₁，x₂，

则

∴ ，所以

得a=1，b= - 4　　　　　　  所以　　 

（20）证明：（Ⅰ）

又x∈（-1，1），所以函数f（x）是奇函数　　　　　 

（Ⅱ）设 -1＜x＜1，△x=x₂- x₁＞0

　

因为1- x₁＞1- x₂＞0；1+x₂＞1+x₁＞0

所以 　　　　　　　　　　　　　　 

所以

所以函数在（- 1，1）上是增函数　　

（21）（Ⅰ）设购买人数为n人，羊毛衫的标价为每件x元，利润为y元，

则

 

∵k＜0，∴x=200时，y_max= - 10000k，

即商场要获取最大利润，羊毛衫的标价应定为每件200元.　　　

（Ⅱ）由题意得，k（x- 100）（x- 300）= - 10000k·75%

所以,商场要获取最大利润的75%,每件标价为250元或150元.