高中数学必修2模块测试试卷B
一、选择题 :(本大题共16小题 ,每小题5分,共80分)
1.若直线![]() 经过原点和点A(-2,-2),则它的斜率为( )
经过原点和点A(-2,-2),则它的斜率为( )
A.-1 B.1 C.1或-1 D.0
2、三个平面把空间分成7部分时,它们的交线有( )
A、1条 B、2条 C、3条 D、1或2条
3.各棱长均为![]() 的三棱锥的表面积为( )
的三棱锥的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
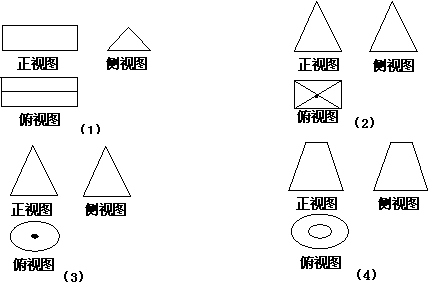 4. 如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
4. 如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
A.三棱台、三棱柱、圆锥、圆台 B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台 D.三棱柱、三棱台、圆锥、圆台
5.经过两点(3,9)、(-1,1)的直线在x轴上的截距为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
6.已知A(1,0,2),B(1,![]() 1),点M在
1),点M在![]() 轴上且到A、B两点的距离相等,则M点坐标为( )
轴上且到A、B两点的距离相等,则M点坐标为( )
A.(![]() ,0,0) B.(0,
,0,0) B.(0,![]() ,0) C.(0,0,
,0) C.(0,0,![]() ) D.(0,0,3)
) D.(0,0,3)
7.如果AC<0,BC<0,那么直线Ax+By+C=0不通过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知圆心为C(6,5),且过点B(3,6)的圆的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
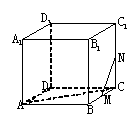 9.在右图的正方体中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
9.在右图的正方体中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30° B.45° C.90° D. 60°
10.给出下列命题
①过平面外一点有且仅有一个平面与已知平面垂直
②过直线外一点有且仅有一个平面与已知直线平行
③过直线外一点有且仅有一条直线与已知直线垂直
④过平面外一点有且仅有一条直线与已知平面垂直
其中正确命题的个数为( )
A.0个 B.1个 C.2个 D.3个
11、圆C1: ![]() 与圆C2:
与圆C2:![]() 的位置关系是( )
的位置关系是( )
A、外离 B 相交 C 内切 D 外切
12、圆:![]() 上的点到直线
上的点到直线![]() 的距离最小值是( )
的距离最小值是( )
A、 2 B、![]() C、
C、![]() D、
D、![]()
13.圆![]() 关于直线
关于直线![]() 对称的圆的方程是( )
对称的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.不论m取任何实数,直线![]() 恒过一定点,则该定点的坐标
恒过一定点,则该定点的坐标
是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15.点![]() 在圆
在圆![]() 内,则直线
内,则直线![]() 和已知圆的公共点的个数为( )
和已知圆的公共点的个数为( )
A.0 B.1 C.2 D.不能确定
16.若圆![]() 上至少有三个不同点到直线
上至少有三个不同点到直线![]() :
:![]() 的距离为
的距离为![]() ,则直线
,则直线![]() 的倾斜角的取值范围是 ( )
的倾斜角的取值范围是 ( )
A.[![]() ]
B.[
]
B.[![]() ]
C.[
]
C.[![]() D.
D.![]()
二. 填空题(每小题4分,共24分)
17.已知圆的圆心在点(1,2),半径为1,则它的标准方程为 .
18.已知球的直径为4,则该球的表面积积为 .
19. 已知圆![]() -4
-4![]() -4+
-4+![]() =0的圆心是点P,则点P到直线
=0的圆心是点P,则点P到直线![]() -
-![]() -1=0的距离是
.
-1=0的距离是
.
20.圆![]() 截直线
截直线![]() 所得的弦长为 。
所得的弦长为 。
21.求过点(2,3)且在x轴和y轴截距相等的直线的方程 .
22.已知圆![]() -4
-4![]() -4+
-4+![]() =0上的点P(x,y),求
=0上的点P(x,y),求![]() 的最大值 .
的最大值 .
三.解答题(本大题共4小题,总分46分)
23.已知两条直线![]() :
:![]() 与
与![]() :
:![]() 的交点
的交点![]() ,求满足下列条件的直线方程
,求满足下列条件的直线方程
(1)过点P且过原点的直线方程;
(2)过点P且垂直于直线![]() :
:![]() 直线
直线![]() 的方程;(10分)
的方程;(10分)
24.已知圆 ![]() 和圆外一点
和圆外一点 ![]() ,求过点
,求过点 ![]() 的圆的切线方程。(10分)
的圆的切线方程。(10分)
25. 如图,ABCD是正方形,O是正方形的中心,PO
如图,ABCD是正方形,O是正方形的中心,PO![]() 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。![]()
求证:(1)PA∥平面BDE
(2)平面PAC![]() 平面BDE
平面BDE
(3)求二面角E-BD-A的大小。(12分)
26.已知方程![]() .
.
(1)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(2)若(1)中的圆与直线![]() 相交于M,N两点,且OM
相交于M,N两点,且OM![]() ON(O为坐标原点)求
ON(O为坐标原点)求![]() 的值;
的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.(14分)
2009届六安二中高三文1、2、8班必修2模块测试试卷B参考答案
一.选择题
BCDCA CCADB DCCBAB
二.填空题
17.![]()
18.16![]()
19.解:由已知得圆心为:![]() ,由点到直线距离公式得:
,由点到直线距离公式得:![]() ;
;
20.![]()
21.x-y+5=0或2x-3y=0
22.![]()
三.解答题
23.解:由![]() 解得
解得![]()
∴ 点P的坐标是(![]() ,2)
,2)
(1)所求直线为y=-x
(2)∵ 所求直线![]() 与
与![]() 垂直,
垂直,
∴ 设直线![]() 的方程为
的方程为 ![]()
把点P的坐标代入得 ![]() ,得
,得![]()
∴ 所求直线![]() 的方程为
的方程为 ![]()
24.![]() 或
或![]()
25.证明(1)∵O是AC的中点,E是PC的中点,∴OE∥AP,
又∵OE![]() 平面BDE,PA
平面BDE,PA![]() 平面BDE,∴PA∥平面BDE
平面BDE,∴PA∥平面BDE
(2)∵PO![]() 底面ABCD,∴PO
底面ABCD,∴PO![]() BD,又∵AC
BD,又∵AC![]() BD,且AC
BD,且AC![]() PO=O
PO=O
∴BD![]() 平面PAC,而BD
平面PAC,而BD![]() 平面BDE,∴平面PAC
平面BDE,∴平面PAC![]() 平面BDE。
平面BDE。
(3)135°
26. 解:(1)![]()
D=-2,E=-4,F=![]()
![]() =20-
=20-![]()
![]()
![]() …………2分
…………2分
(2)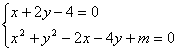
![]() 代入得
代入得
![]() ………..3分
………..3分
![]() ,
,![]() ……………4分
……………4分
∵OM![]() ON
ON
得出:![]() ……………5分
……………5分
∴![]()
∴![]() …………….7分
…………….7分
(3)设圆心为![]()
![]() …………….8分
…………….8分
半径![]() …………9分
…………9分
圆的方程![]() ……………10分
……………10分