高中数学必修五综合练习4
考号 班级 姓名
一.选择题(本大题共10个小题,每小题5分,满分50分,)
1.不在 3x+ 2y < 6 表示的平面区域内的一个点是
A(0,0) B(1,1) C(0,2) D (2,0)
2.如果a、x1、x2、b成等差数列,a、y1、y2、b成等比数列,那么![]() 等于
等于
A ![]() B
B ![]() C
C
![]() D
D ![]()
3.若![]() ,则
,则
A ![]() B
B
![]() C
C ![]() D
D
![]()
4.数列![]() 则
则![]() 是该数列的
是该数列的
A 第6项 B 第7项 C 第10项 D 第11项
5.抛物线y=ax2+bx+c与x轴的两个交点为(![]() , 0), (
, 0), (![]() , 0),则ax2+bx+c>0的解的情况是
, 0),则ax2+bx+c>0的解的情况是
A ![]() <x<
<x<![]() B x>
B x>![]() 或x<
或x<![]() C x≠±
C x≠±![]() D 不确定,与a的符号有关
D 不确定,与a的符号有关
6. 若![]() 且
且![]() ,则下列四个数中最大的是
,则下列四个数中最大的是
 A
A ![]() B
B![]()
![]() C 2ab D
C 2ab D![]()
7.如图,为了测量隧道两口之间AB的长度,对给出的四组数据,计算时要求最简便,测量时要求最容易,应当采用的一组是
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
8.已知![]() ,则
,则![]() 的最小值为
的最小值为
A 8
B 6
C ![]() D
D ![]()
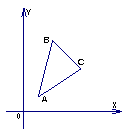 9.给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3),若使目标函数
9.给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3),若使目标函数![]() 取得最大值的最优解有无穷多个,则a的值是
取得最大值的最优解有无穷多个,则a的值是
A ![]() B 1 C
4 D
B 1 C
4 D ![]()
10.下列函数中,最小值为4的有多少个?
① ![]() ②
② ![]()
![]() ③
③ ![]() ④
④ ![]()
A.4 B.3 C.2 D.1
二.填空题(本大题共4个小题,每小题5分,满分20分,把答案填在答题卷中相应的空格中)
11.不等式![]() 的解集是
,
的解集是
,
12.在![]() 中,
中,![]() ,则最短边的长是
,
,则最短边的长是
,
13.约束条件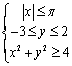 构成的区域的面积是
平方单位,
构成的区域的面积是
平方单位,
14.等差数列{an}中,Sn是它的前n项之和,且S6<S7,S7>S8,则
①比数列的公差d<0 ②S9一定小于S6
③a7是各项中最大的一项 ④S7一定是Sn中的最大值
其中正确的是 (填入你认为正确的所有序号)
三.解答题(满分80分)
15.(本小题12分)在等比数列![]() 中,
中,![]() ,公比
,公比![]() ,前
,前![]() 项和
项和![]() ,求首项
,求首项![]() 和项数
和项数![]() .
.
16.(本小题13分)若不等式![]() 的解集是
的解集是![]() ,求不等式
,求不等式![]() 的解集.
的解集.
17.(本小题13分)某工厂要建造一个无盖长方体水池,底面一边长固定为8![]() ,最大装水量为72
,最大装水量为72![]() ,池底和池壁的造价分别为
,池底和池壁的造价分别为![]() 元
元![]() 、
、![]() 元
元![]() ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
18.(本小题14分)某工厂要制造A种电子装置41台,B种电子装置66台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2㎡,可做A、B的外壳分别为2个和7个,乙种薄钢板每张面积5㎡,可做A、B的外壳分别为7个和9个,求两种薄钢板各用多少张,才能使总的用料面积最小?

19.(本小题14分)在等差数列![]() 中,
中,![]() ,前
,前![]() 项和
项和![]() 满足条件
满足条件![]() ,
,
(1)求数列![]() 的通项公式和
的通项公式和![]() ;
;
(2)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]()
![]()
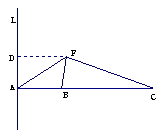
20.(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.
(1)设A到P的距离为![]() km,用
km,用![]() 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求![]() 值;
值;
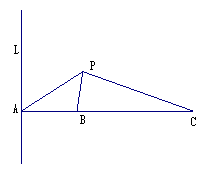 (2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)。
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)。
文1、2、8专用必修五综合练习4参考答案及评分标准
一.选择题(每小题5分,满分50分,把正确答案的代号填在答题卷的相应表格中)
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | C | B | D | B | A | C | A | D |
二.填空题(每小题5分,满分20分,把答案填在下面的空格中)
11 ![]() , 12 2 ,13
, 12 2 ,13 ![]() ,14 ①②④ 。
,14 ①②④ 。
三.解答题(满分80分)
15.(本小题12分)
解:由已知,得
|
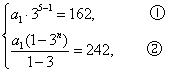
由①得![]() ,解得
,解得![]() . …………9分
. …………9分
将![]() 代入②得
代入②得![]() ,
,
即
![]() ,解得 n=5. ………11分
,解得 n=5. ………11分
∴数列![]() 的首项
的首项![]() ,项数n=5. ………12分
,项数n=5. ………12分
16.(本小题满分13分)
解:由已知条件可知![]() ,且
,且![]() 是方程
是方程![]() 的两个根,…3分
的两个根,…3分
由根与系数的关系得 ,解得
,解得![]() ……………………………6分
……………………………6分
所以![]() 变为
变为![]() …………………………8分
…………………………8分
![]() ………………………10分
………………………10分
![]() ……………………12分
……………………12分
即不等式![]() 的解集是
的解集是![]() ………………13分
………………13分
17.(本小题13分)
解:设池底一边长为![]() ,水池的高为
,水池的高为![]() ,池底、池壁造价分别为
,池底、池壁造价分别为![]() ,则总造价为
,则总造价为
![]() ………………………2分
………………………2分
由最大装水量知![]() ,
,![]() ………………………3分
………………………3分
![]() ………………………5分
………………………5分
![]() ………………………7分
………………………7分
![]()
![]()
![]() ………………………10分
………………………10分
当且仅当![]() 即
即![]() 时,总造价最低,
时,总造价最低,![]() …………12分
…………12分
答:将水池底的矩形另一边和长方体高都设计为![]() 时,总造价最低,最低造价为
时,总造价最低,最低造价为![]() 元。
………………………13分
元。
………………………13分
18.(本小题14分)
解:设甲乙两种薄钢板各用![]() 张,用料总面积为
张,用料总面积为![]() ,则目标函数为
,则目标函数为
![]() ,
………………………2分
,
………………………2分
约束条件为 : ………………………5分
………………………5分
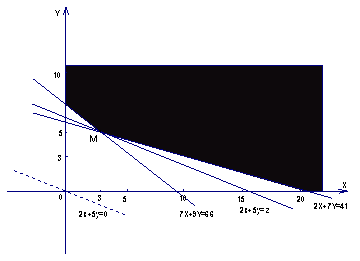 作出约束条件的可行域如图:
作出约束条件的可行域如图:
………………………………………………8分
作直线![]() :
:![]() ,平移,观察知,当
,平移,观察知,当![]() 经过点
经过点![]() 时,
时,![]() 取到最小值。……10分
取到最小值。……10分
解方程组![]() ,得
,得![]() 点坐标为
点坐标为![]() ………………………12分
………………………12分
所以![]() ㎡
………………………13分
㎡
………………………13分
答:甲种钢板用3张,乙种钢板用5张,能够使总的用料面积最小。 ……14分
19.(本小题14分)
解:(1)设等差数列![]() 的公差为
的公差为![]() ,由
,由![]()
得:![]() ,所以
,所以![]() ,且
,且![]() , …………………3分
, …………………3分
所以![]()
![]() …………………5分
…………………5分
![]() …………………………6分
…………………………6分
(2)由![]() ,得
,得![]()
![]()
所以![]() , ……①………………8分
, ……①………………8分
![]() , …… ②…………10分
, …… ②…………10分
①-②得
![]() ……………12分
……………12分
![]()
![]() ………………………………13分
………………………………13分
所以
![]() ……………………………………14分
……………………………………14分
20.(本小题14分)
解:(1)依题意,
![]() (km),
…………2分
(km),
…………2分
![]() (km). …………4分
(km). …………4分
因此 ![]() ………………5分
………………5分
在△PAB中,AB= 20 km,
![]() ………7分
………7分
同理,在△PAC中,![]() ………………………8分
………………………8分
由于![]() ………………………9分
………………………9分
 即
即![]() 解得
解得![]() (km). …………………………10分
(km). …………………………10分
(2)作PD![]() L,垂足为D. 在Rt△PDA中,
L,垂足为D. 在Rt△PDA中,
PD =PAcos∠APD=PAcos∠PAB
=  …………12分
…………12分
![]() (km). ………………………13分
(km). ………………………13分
答:静止目标P到海防警戒线L的距离约为17. 71 km. …………………14分