高三理科数学上册期末试卷
命题、校对:孟伟强、陈连原
一、选择题:(本大题共10小题,每小题4分,共40分)
1.在复平面内,复数![]() 对应的点位于
( )
对应的点位于
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.“a=![]() ”的
( )
”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分条件也不是必要条件
3.已知![]() 为两条直线,则下列条件中可以判断平面
为两条直线,则下列条件中可以判断平面![]() 与平面
与平面![]() 平行的是
平行的是
A.![]() B.
B.![]() ( )
( )
C.![]() D.
D.![]()
4.设![]() , 则此函数在区间
, 则此函数在区间 ![]() 和
和![]() 内分别为 ( )
内分别为 ( )
A.单调递增,单调递增 B.单调递增,单调递减
C.单调递减,单调递增 D.单调递减,单调递减
5.在数列![]() 中,
中,![]() ,当n≥2时,
,当n≥2时,![]() ,且已知此数列有极限,则
,且已知此数列有极限,则![]()
等于 ( )
A.-2 B.
6.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D,
D,![]() ( )
( )
7.若![]() 且
且![]() ,那么
,那么![]() 的最小值是 ( )
的最小值是 ( )
A.2 B.![]() C.
C.![]() D.0
D.0
8.若函数![]() 满足
满足![]() , 且
, 且![]() 时
时![]() ,则函 数
,则函 数![]() 的图象与函数
的图象与函数![]() 的图象的交点个数为 ( )
的图象的交点个数为 ( )
A.16 B.
9.设![]() , 则对任意正整数
, 则对任意正整数![]() , 都成立的不等式
, 都成立的不等式
是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 10.若函数
10.若函数![]() 的图象如图所示,则m的范围为 ( )
的图象如图所示,则m的范围为 ( )
A.(-∞,-1)
B.(-1,2)
C.(1,2)
D.(0,2)
二、填空题:(本大题共4小题,每小题4分,共16分)
11.国家准备出台调整个人收入所得税方面的政策,各地举行各行业收入的入户调查.某住宅小区约有公务员120,公司职员200人,教师80人,现采用分层抽样的方法抽取容量为20人的样本进行调查,则公务员、公司职员、教师各
抽取的人数为 ;
12.函数![]() 的图象中相邻两条对称轴的距离是______
;
的图象中相邻两条对称轴的距离是______
;
13.若![]() ,则
,则
![]() .(用数字作答)
.(用数字作答)
14.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内
每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示.据图中提供的信息,回
为常数),如图所示.据图中提供的信息,回
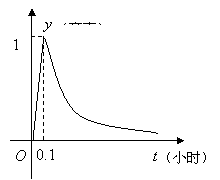 答下列问题:
答下列问题:
⑴从药物释放开始,每立方米空气中的含药量
![]() (毫克)与时间
(毫克)与时间![]() (小时)之间的函数关系
(小时)之间的函数关系
式为 ;
⑵据测定,当空气中每立方米的含药量降低到
![]() 毫克以下时,学生方可进教室,那么药
毫克以下时,学生方可进教室,那么药
物释放开始,至少需要经过 小时
后,学生才能回到教室.
三、解答题:(本大题共5题,满分44分)
15.(本题满分8分)从6名男同学和4名女同学中随机选出3名同学参加一项竞技测
试,每位同学通过测试的概率为0.7,试求:
⑴选出的三位同学中同学甲被选中并且通过测试的概率;
⑵设选出的三位同学中男同学的人数为![]() ,求
,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
16.(本题满分8分)已知函数![]() (
(![]() ) ,
) ,
⑴试确定![]() 的单调区间 , 并证明你的结论 ;
的单调区间 , 并证明你的结论 ;
⑵若![]() 时 , 不等式
时 , 不等式![]() 恒成立 , 求实数
恒成立 , 求实数![]() 的取值范围 .
的取值范围 .
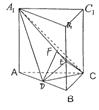
 17.(本题满分8分)在直三棱柱ABC—A1B
17.(本题满分8分)在直三棱柱ABC—A1B
⑴求证:CD⊥平面A1ABB1;
⑵求二面角C—A1E—D的大小.
18.(本题满分10分)已知数集序列{1}, {3, 5}, {7, 9,11}, {13, 15, 17, 19},……, 其中第n个集合有n个元素,每一个集合都由连续正奇数组成,并且每一个集合中 的最大数与后一个集合最小数是连续奇数;
⑴ 求第n个集合中最小数an的表达式;
⑵求第n个集合中各数之和Sn的表达式;
⑶令f(n)=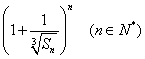 ,求证:2≤
,求证:2≤![]() .
.
19.(本题满分10分)设![]() 、
、![]() ∈R,常数
∈R,常数![]() ,定义运算“
,定义运算“![]() ”:
”:
![]() ,定义运算“
,定义运算“![]() ”:
”:![]() ;对于
;对于![]() 、
、
![]() ,定义
,定义![]() ;
;
⑴若![]() ≥0,求动点P(
≥0,求动点P(![]() ,
,![]() ) 的轨迹;
) 的轨迹;
⑵已知直线![]() 与(Ⅰ)中轨迹C交于
与(Ⅰ)中轨迹C交于![]() 、
、![]() 两点,若
两点,若![]() ,试求
,试求![]() 的值;
的值;
⑶若直线![]() 不过原点且与
不过原点且与![]() 轴交于点S,与
轴交于点S,与![]() 轴交于点T,并且与(1)中轨迹C交 于两点P、Q , 试求
轴交于点T,并且与(1)中轨迹C交 于两点P、Q , 试求![]() 的取值范围。
的取值范围。
参考答案
一、选择题:每小题4分,满分40分.
1.D 2.A 3.B 4.C 5.C
6.A 7.B 8.B 9.C 10.C
二、填空题:每小题4分,满分16分.
11.6、10、4 12.![]() 13.2008 14.
13.2008 14. 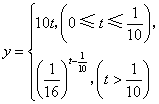 ;0.6
;0.6
三、解答题: 本大题共5小题,共44分.
15.解(1)同学甲被选中的概率为![]() ---------------2分
---------------2分
则同学甲被中且通过测试的概率为0.3×0.7=0.21 ----------4分
(2)根据题意,![]() 的可能取值为0、1、2、3,
的可能取值为0、1、2、3,
![]()
![]()
|
![]() ------------8分
------------8分
(注:分布列给3分,错一个扣1分)
16. 解:(1)当![]() 时 ,
时 , ![]() , ------------2分
, ------------2分
令![]() 可得
可得![]() ; 令
; 令![]() 可得
可得![]() .
.
∴函数![]() (
(![]() )在区间
)在区间![]() 上是增函数; 在区间
上是增函数; 在区间![]() 上是减函数 4分
上是减函数 4分
(2)由(1)得,函数函数![]() (
(![]() )在区间
)在区间![]() 上是增函数 ,
上是增函数 ,
∴当![]() 时,
时, ![]() .-------6分
.-------6分
∵不等式![]() 恒成立 , ∴
恒成立 , ∴![]() , 解之得
, 解之得 ![]() .-----8分
.-----8分
17.证明:(1)设AD=![]() ,则BD=
,则BD=![]() 从而
从而![]()
DE2=(![]()
由∠A1DE=90°,得![]()
|
∴D为AB的中点,于是CD⊥AB.--------4分
又平面ABC⊥平面A1ABB1,所以CD⊥平面A1ABB1.
解:(2)过D作DF⊥A1E,垂足为F,连结CF,则CF⊥A1E,
故∠CFD为二面角C—A1E—D的平面角.
∵![]() ∴∠CFD=45°.------8分
∴∠CFD=45°.------8分
18.解:(1)设第n个集合中最小数an , 则第![]() 个集合中最小数
个集合中最小数![]() ,
,
又第![]() 个集合中共有
个集合中共有![]() 个数, 且依次增加2 ,
个数, 且依次增加2 ,
∴![]() ,即
,即 ![]() ,
,
∴![]()
![]()
![]() ,
,
相加得![]() , 又
, 又![]() ∴
∴![]() --3分
--3分
(2)由(1)得![]() , 从而得
, 从而得![]() ------5分
------5分
(3)由(2)得![]() , ∴
, ∴
![]() ,
,
∵![]() ≥
≥![]() ---7分
---7分
又当![]() ≥2 时,
≥2 时, ![]() ≤
≤![]()
∴![]()
≤![]()
![]() .
.
∴ 2≤![]() -----------------------------------10分
-----------------------------------10分
19.解:(1) 设![]() ,
,
则![]() , 又由
, 又由![]() ≥0 ,
≥0 ,
可得P(![]() ,
,![]() ) 的轨迹为
) 的轨迹为![]() ; -----3分
; -----3分
(![]() 范围不写扣1分)
范围不写扣1分)
(2) 由已知可得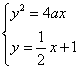 , 整理得
, 整理得![]()
由![]() 得
得![]() .
∵
.
∵![]() , ∴
, ∴![]() .
.
∴![]()
![]() , 解得
, 解得![]() ---------6分
---------6分
(3) ∵![]() ,
,
∴![]()
设直线![]() , 依题意
, 依题意![]() ,
, ![]() ,则
,则![]()
分别过P、Q作PP1⊥ y轴,1⊥ y轴,垂足分别为P1、Q1,
则![]()
![]() .
.
由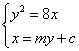 消去y ,得
消去y ,得![]() .
.
∴![]() ≥
≥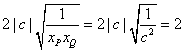 .
.
∵![]() 、
、![]() 可取一切不相等的正数,∴
可取一切不相等的正数,∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() )-10分
)-10分