高中数学必修2立体几何部分试卷2008-4-21

试卷满分100分。时间70分钟　考号　　　班级　　　 姓名　　　　 

第Ⅰ卷（选择题　共40分）

一、选择题：本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1、垂直于同一条直线的两条直线一定　（　　）

A、平行　　　　　 B、相交　　　　　　　C、异面　　　　  D、以上都有可能

2、过直线外两点作与直线平行的平面，可以作（　 ）

　  A．1个　 　　 B．1个或无数个　　C．0个或无数个 　 D．0个、1个或无数个

3、正三棱锥底面三角形的边长为，侧棱长为2，则其体积为　　　　　　　　　　　　　　（　　）

　　　A． 　　　　　　　　　　　B． 　　　　　　　　　C．　　　　　　　　　　　D．

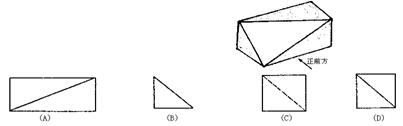
4、右图是一个实物图形，则它的左视图大致为　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

5、已知正四棱台的上、下底面边长分别为3和6，其侧面积等于两底面积之和，则该正四棱台的高是　　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．2　　　　　　　　　　　　B．　　　　　　　　　　　C．3　　　　　　　　　　　　D．

6、已知、是平面，m、n是直线，则下列命题不正确的是　　　　　　　　　 　（　　 ）

A．若，则　　　　  B．若，则

C．若，则　 D．若，则

7、正六棱柱ABCDEF－A₁B₁C₁D₁E₁F₁的侧面是正方形，若底面的边长为a，则该正六棱柱的外接球的表面积是　(　　 )

A．4πa²　　　　  B.5 πa²　　　　  C. 8πa²　　　　 D.10πa²

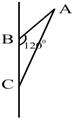
8、如右下图，在中，，，，如图所示。若将绕旋转一周，则所形成的旋转体的体积是（　　）　　　　　　　　　　　　　　　　　　 

（A） 　　　　（B）　　　　  （C）　　　　  （D）　

　　　　　　　　　　　　　　　　　　　　 （第8题图）

9、如左上图是由单位立方体构成的积木垛的三视图，据此三视图可知，构成这堆积木垛的单

　 位正方体共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．6块　　　　　　　　 B．7块　　 　　　　　C．8块　　 　　　　　　 D．9块

10、给出下列命题

①过平面外一点有且仅有一个平面与已知平面垂直

②过直线外一点有且仅有一个平面与已知直线平行

③过直线外一点有且仅有一条直线与已知直线垂直

④过平面外一点有且仅有一条直线与已知平面垂直

其中正确命题的个数为（　　）

A．0个　　　　　　 B．1个　 　　　　　　　　　　C．2个　　 　　　　　D．3个

第Ⅱ卷（非选择题　共60分）

二、填空题（每小题4分，共16分）

11、已知直线m、n及平面，其中m∥n，那么在平面内到两条直线m、n距离相等的点的集合可能是：①一条直线；②一个平面；③一个点；④空集。

其中正确的是　　　　　　　　　　。

12、一个正四棱柱的各个顶点在一个直径为2cm的球面上．如果正四棱柱的底面边长为1cm，那么该棱柱的表面积为　　　　　 cm．

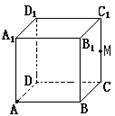
13、如右图．M是棱长为2cm的正方体ABCD-A₁B₁C₁D₁的棱CC₁的中点，沿正方体表面从点A到点M的最短路程是　　　 cm．

14、已知两条不同直线、，两个不同平面、，给出下列命题：

①若垂直于内的两条相交直线，则⊥；

②若∥，则平行于内的所有直线；

③若，且⊥，则⊥；

④若，，则⊥；

⑤若，且∥，则∥；

其中正确命题的序号是　　　　　　　　 ．（把你认为正确命题的序号都填上）

三解答题：（本题共4小题，共44分）

15、（本小题10分）已知在三棱锥S--ABC中，∠ACB=90⁰，又SA⊥平面ABC，

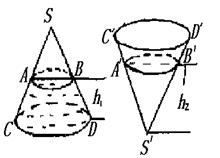
AD⊥SC于D，求证：AD⊥平面SBC，

16、（本小题10分）如图，圆锥形封闭容器，高为h，圆锥内水面高为若将圆锥倒置后，圆锥内水面高为

17、（本小题满分10分）

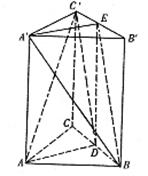
如图，在三棱柱—中，点D是BC的中点，欲过点作一截面与平面　平行，问应当怎样画线，并说明理由。

18、（本小题14分）已知四棱锥P-ABCD，底面ABCD是、边长为的菱形，又，且PD=CD，点M、N分别是棱AD、PC的中点．

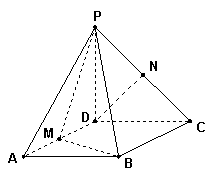　 （1）证明：DN//平面PMB；

　 （2）证明：平面PMB平面PAD；

　 （3）求点A到平面PMB的距离．

2009届六安二中高三文1、2、8班必修2立体几何部分试卷答案　

一.选择题（每小题4分，10个小题共40分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	D	C	D	A	D	B	D	B	B

二.填空题（每小题4分，4个小题共16分）

11.　 ①②④　 .　　　　　　　　　　　 12..

13..　　　　　　　　　　　　　　　 14. ①④　.

三.解答题（第15、16小题每小题10分, 第17题12分、18小题14分,共44分）

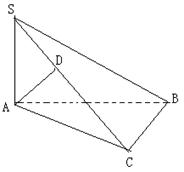15、（本小题10分）

证明：SA⊥面ABC， BC⊥面ABC，Þ BC ⊥SA；

又BC⊥AC，且AC、SA是面SAC内的两相交线，∴BC⊥面SAC；

又ADÌ面SAC，∴ BC⊥AD，

又已知SC⊥AD，且BC、SC是面SBC内两相交线，∴ AD⊥面SBC。

16、（本小题10分）

分析：圆锥正置与倒置时，水的体积不变，另外水面是平行于底面的平面，此平面截得的小圆锥与原圆锥成相似体，它们的体积之比为对应高的立方比.

　　　 解：

　　　　　　　　　　　　　　　　　　　

17、（本小题满分12分）

解：（Ⅰ）取的中点E，连结，

则平面∥平面……………………4分

∵D为BC的中点，E为的中点，∴

　　又∵BC∥，∴四边形为平行四边形，

　　　 ∴∥BE，……………………………………7分

连结DE，则DE　　，

∴DE　　,

∴四边形是平行四边形，

∴AD∥……………………………………………………………10分

又∵ 平面，，∴平面∥平面。………12分　　

18、（本小题14分）

解：（1）证明：取PB中点Q，连结MQ、NQ，因为

M、N分别是棱AD、PC中点，所以

　　　  QN//BC//MD，且QN=MD，于是DN//MQ.

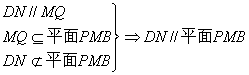.…　　　 …………………6分

　 （2）

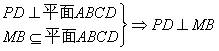
又因为底面ABCD是、边长为的菱形，且M为AD中点，

所以.又所以.

………………10分

　 （3）因为M是AD中点，所以点A与D到平面PMB等距离.

过点D作于H，由（2）平面PMB平面PAD，所以.

　　　 故DH是点D到平面PMB的距离.

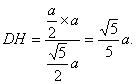所以点A到平面PMB的距离为.………14分