一、排列与组合
类型一、“数”的方面
（一）、选择题
一、【高考真题】
1（04年全国2卷）在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（ C ）
A．56个 B．57个 C．58个 D．60个
3（06年北京3）在1，2，3，4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有（B）
（A）36个 （B）24个 （C）18个 （D）6个
2（04年辽宁12）有两排座位，前排11个座位，后排12个座位，现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同排法的种数是（B）
A．234 B．346 C．350 D．363
3（05年湖北9）把一排6张座位编号为1，2，3，4，5，6的电影票全部分给4个人，每人至少分1张，至多分2张，且这两张票具有连续的编号，那么不同的分法种数是（ D ）
A．168 B．96 C．72 D．144
4（05年江西文7）将9个（含甲、乙）平均分成三组，甲、乙分在同一组，则不同分组方法的种数为（A）
A．70 B．140 C．280 D．840
5（02年北京9）5本不同的书，全部分给四个学生，每个学生至少1本，不同分法的种数为（B）
A．480 B．240 C．120 D．96
6（04年全国3卷12）将4名教师分配到3所中学任教，每所中学至少1名，则不同的分配方案有（C）
A．12种 B．24种 C．36种 D．48种
7（04年江苏3）从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法有（ D）
A．140种 B．120种 C．35种 D．34种
8（05年北京7）北京《财富》全球论坛期间，某高校有14名志愿者参加接待工作，若每天排早、中、晚三班，每4人，每人每天最多值一班，则开幕式当天不同的排班种数为（ A ）
A．
B．
C．
D．
9（04年福建6）某校高二年级共有六个班级，现从外地转入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为（ C ）
A．
B．
C．
D．
10。12名同学分别到三个不同的路口进行车流量的调查，若每个路口4人，则不同的分配方案共有（A）
A．
种 B．
种 C．
种 D．
种（02年北京9）
11（03年北京8）从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，不同的种植方法共有（ C ）
A．24种 B．18种 C．12种 D．6种
12．（03年北京春）某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目.如果将这两个节目插入原节目单中，那么不同插法的种数为（ A ）
A．42 B．30 C．20 D．12
13（05年福建9）从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一人游览，每人只游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有（ B ）
A．300种 B．240种 C．144种 D．96种
14一题作答，选甲题答对得100分，答错得－100分；选乙题答对得90分，答错得－90分.若4位同学的总分为0，则这4位同学不同得分情况的种数是（ B ）
A．48 B．36 C．24 D．18
|
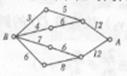
数字表示该段网线单位时间内可以通过的最大信息量.
现从结点A向结点B传递信息，信息可以分开沿不同
的路线同时传递，则单位时间内传递的最大信息量为（D）
（A）26 （B）24 （C）20 （D）1
16（01年江西9）某赛季足球比赛的计分规则是：胜一场，得3分；平一场，得1分；负一场，得0分.
一球队打完15场，积33分，若不考虑顺序，该队胜、负、平的情况共有（A）
（A）3种 （B）4种 （C）5种 （D）6种
二、【模拟试题】
.25人排成5×5方阵，从中选出3人，要求其中任意2人不同行也不同列，则不同的选出方法种数为（ A ）
（A）600 （B）300 （C）100 （D）60
9. 某公司新招聘进8名员工，平均分配给下属的甲、乙两个部门，其中两名英语翻译人员不能分在同一个部门，另外三名电脑编程人员也不能分在同一个部门，则不同的分配方案共有（ A ）
A. 36种 B. 38种 C. 108种 D. 24种
9．某旅馆有三人间，两人间，单人间三种房间各一间，有三位成人带两个小孩来此投宿，
小孩子不宜单住一间（必须有成人陪同），则不同的安排住宿方法有YC（ B ）
A．35种 B．27种 C．21种 D．18种
11．从5位男同学和4位女同学中选出3位同学分别担任数、语、外三科的科代表，要求选出的3位同学中男女都要有，则不同的选派方案共有（ C ）
A．210种 B．630种 C．420种 D．840种
6.8个人坐成一排，现要调换其中3个人中每一个人的位置，其余5个人的位置不变，则不同的调换方式有（ B ）
A．C
B.CA
C. CA
D.3C
8一条长椅上有9个座位，若3个人坐，要求相邻2人之间至少有2个空椅子，则共有（C）种不同的坐法。
A、84 B、72 C、60 D、48
10．对某种产品的6件不同正品和4件不同次品一一进行测试，到区分出所有次品为止，若所有次品恰好在第五次测试被全部发现，则这样的测试方法有（ C ）种.
A．24 B．96 C．576 D．720
10．现有A、B、C、D、E、F、G、H8位同学站成一排照像，要求同学A、B相邻，C、D相邻，而G、H不相邻，这样的排队照像方式有（ D ）
A．36种 B．48种 C．42种 D．1920种
7．有8辆不同型号的小轿车在车展上排成一排，英才苑其中甲、乙、丙三辆车不能同时相邻的排法数有（D）
A．
B．
C．
D．
8．某电视台邀请了6位同学的父母共12人，请这12位家长中的4位介绍教育子女的情况，那么这4位中至多一对夫妻的选择方法为（ D ）
A．15种 B．120种 C．240种 D．480种
（二）、填空题
一、【高考真题】
1（05年全国2卷15）在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被5整除的数共有 192 个.
2（04年天津16） 从1，3，5，7中任取2个数字，从0，2，4，6，8中任取2个数字，组成没有重复数字的四位数，其中能被5整除的四位数共有 300个.（用数字作答）
3（05年浙江14）从集合{O，P，Q，R，S}与{0，1，2，3，4，5，6，7，8，9}中各任取2个元素排成一排（字母和数字均不能重复）.每排中字母O、Q和数字0至多只出现一个的不同排法种数是8424（用数字作答）.
4（04年湖北14）将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子内，每个盒内放一个球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 240种.
5（05年辽宁15）用1、2、3、4、5、6、7、8组成没有重复数字的八位数，要求1和2相邻，3与4相邻，5与6相邻，而7与8不相邻，这样的八位数共有 576 个.（用数字作答）
15．从6种不同的蔬菜种子a、b、c、d、e、f中选出四种，分别种在四块不同的土壤A、B、C、D中进行试验，已有资料表明：A土壤不宜种a，B土壤不宜种b，但a、b两品种高产，现a、b必种的试验方案 84种.
二、【模拟试题】
16．从5名男生和4名女生中选出4人参加某活动，如果男生甲和男生乙至少有一人在内，女生丙必须在内，则选择种数是 36 .
15．三位数中，如果十位上的数字比个位上、百位上的数字都要小，则称这个数为凹数，如524、317等都是凹数，那么，各数位上无重复数字的三位凹数共有_240____个.
14．用0，1，2，3，4这五个数字组成没有重复数字的五位数，其中恰好有一个偶数数字夹在两个奇数数字之间的五位数的个数是（用数字作答） 28
对于各数互不相等的正数数组
（
是不小于
的正整数），如果在
时有
，则称
与
是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为此数组的“逆序数”。例如，数组
中有逆序“2，1”，“4，3”，“4，1”，“3，2”，其“逆序数”等于4。若各数互不相等的正数数组
的“逆序数”是2，则
的“逆序数”是 
。
13．⑴“渐升数”是指每个数字比其左边的数字大的正整数(如34689)，则五位“渐升数”共有______个。
⑵若把所有五位数渐升数按小到大的顺序排列，则第100个数为_________ .
答案：⑴C48＋C47＋C46＋C45+1=126 ⑵ 24789
8. 由三个数字1，2，3组成的五位数中, 1，2，3都至少出现
次, 这样的
位数共有 150 个.
（分类：出现一次，有 
；出现 二次，有
；出现三次，有 
．则这样的五位数共有 
个）
|
10．将1、2、3、……、8、9这九个数字填写在如图的9个空格子中，
要求每一行从左到右依次增大，每列从上到下也依次增大，当
数字4固定在中心位置时，则所有填写空格的方法有 种。
答案：12
类型二、“形”的方面
（一）选择题
一、【高考真题】
1（05年湖南文7）设直线的方程是
，从1，2，3，4，5这五个数中每次取两个不同的数作为A、B的值，则所得不同直线的条数是（ C ）
A．20 B．19 C．18 D．16
2（05年天津6）从集合{1,2,3…，11}中任选两个元素作为椭圆方程
中的m和n,则能组成落在矩形区域B={(x,y) x<11且y<9}内的椭圆个数为（ B ）
A．43 B． 72 C． 86 D． 90
3（04年北京7）从长度分别为1，2，3，4，5的五条线段中，任取三条的不同取法共有n种。在这些取法中，以取出的三条线段为边可组成的钝角三角形的个数为m，则
等于（B）
A．
B．
C． 
D． 
4（02年全国文12）从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有（B）
A．8种 B．12种 C．16种 D．20种
5（04年湖南10）从正方体的八个顶点中任取三个点为顶点作三角形，其中直角三角形的个数为（ C ）
A．56 B．52 C．48 D．40
6（05年江苏12）四棱锥的8条棱代表8种不同的化工产品，有公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共顶点的两条棱多代表的化工产品放在同一仓库是安全的，现打算用编号为①、②、③、④的4个仓库存放这8种化工产品，那么安全存放的不同方法种数为（ B ）
A．96 B．48 C．24 D．0
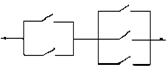
二、【模拟试题】
7．如图所示，断开一些开关使A到B的电路不通的不同方法共有（ C ）
A．6种 B．8种 C．11种 D．12种
10．已知三角形ABC的各边为互不相等的正整数，其中最长边为11，则满足条件的所有不同的三角形共有 （ B ）
A．18个 B．20个 C．25个 D．45个
10．已知直线
（a，b不全为0）与圆
有公共点，且公共点的横、纵坐标均为整数，那么这样的直线共有（ B ）
A．28条 B．32条 C．36条 D．40条
10．用四种不同的颜色给正方体ABCD—A1B1C1D1的六个面染色，要求相邻两个面涂不同的颜色，且四种颜色均用完，则所有不同的涂色方法共有（ C ）
A．24种 B．96种 C．72种 D．48种
11．将正方体ABCD－A1B1C1D1的各面涂色，任何相邻两个面不同色，现在有5个不同的颜色，并且涂好了过顶点A的3个面的颜色，那么其余3个面的涂色方案共有（ C ）
A．15种 B．14种 C．13种 D．12种
10．以正方体的顶点为顶点构成的四棱锥与三棱锥个数之差的绝对值为 （ A ）
A．10 B．22 C．34 D．46
6．球面上有七个点，其中四个点在同一个大圆上，其余再无三点共一个大圆，也无两点与
球心共线，那么经过这七个点的球的大圆有（ B ）
A．15个 B．16个 C．31个 D．32个
（二）填空题
一、【高考真题】
1（01年全国16）圆周上有2n个等分点（n>1）,以其中三个点为顶点的直角三角形的个数为 2n(n-1)
|
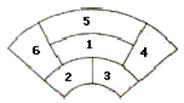
为6个部分（如图）.现要栽种4种不同颜色的花，每部分栽种一
种且相邻部分不能栽种同样颜色的花，不同的栽种方
|
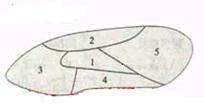
3（03年全国15）如图，一个地区分为5个行政区域，
现给地图着色，要求相邻区
域不得使用同一颜色，现有4种颜色可供选择，则不同
的着色方法共有 72 种.（以数字作答）
4（04年浙江15）设坐标平面内有一个质点从原点出发，沿x轴跳动，每次向正方向或负方向跳1个单位，经过5次跳动质点落在点（3，0）（允许重复过此点）处，则质点不同的运动方法共有5种（用数字作答）.
5（05年北京春13）从
这四个数中选三个不同的数作为函数
的系数，可组成不同的二次函数共有_18_个，其中不同的偶函数共有_6个．（用数字作答）
二、【模拟试题】
16．直线x=m, y=x将圆面x2+y2≤4分成若干块，现在用5种不同的颜色给这若干块涂色，每块只涂一种颜色，且任意两块不同色，若共有120种不同的涂法，则实数m的取值范围是