数学理科 模拟试卷二
一、选择题
1. 设集合M={1,2}, N={2,3},则满足P(M∪N)的集合P的个数是:( )
(A) 6个 (B) 7个
(C) 8个 (D) 9个
2. 有一分币3枚,两角币6张,十元币4张,可组成不同的币值( )
(A) 139种 (B)72种
(C) 444种 (D)1080种
3. 设α,β都是第二象限角,若sinα>sinβ, 则:( )
(A) tgα>tgβ (B) ctgα<ctgβ
(C) cosα>cosβ (D) secα>secβ
4. 已知
(1-2x)![]() 的展开式中,奇数项的二项式系数之和为32,则该二项式展
的展开式中,奇数项的二项式系数之和为32,则该二项式展
开式的中间项为:( )
(A) -160x![]() (B) 160x
(B) 160x![]()
(C) 240x![]() (D) -160x
(D) -160x![]() 与240x
与240x![]()
5. 直线![]()
![]() (t是参数)的倾角为( )
(t是参数)的倾角为( )
(A) π-arctg2 (B) arctg(-2)
(C) π-arctg![]() (D) arctg(-
(D) arctg(-![]() )
)
6. 函数 ![]() (x<0) ( )
(x<0) ( )
(A) 有最小值3
(B) 有最小值 ![]()
(C) 有最大值3 (D)
有最大值![]()
7. 平移坐标系,将坐标原点平移到曲线x![]() -3y
-3y![]() -4x-6y-2=0的中心,则在新坐标系中,
-4x-6y-2=0的中心,则在新坐标系中,
点(1,2)在原坐标系中的坐标为:( )
(A) (-1,3) (B) (-1,5)
(C) (3,1) (D) (3,-4)
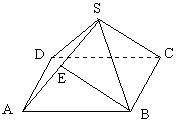
| 8. 设正四棱锥S-ABCD的侧棱之长为
BE与SC所成的角等于( ) |
(A) 30° (B) 45°
(C) 60° (D) 90°
9. 设在甲、乙、丙三个宿舍中,每个宿舍住3个同学,现从这9个中选出3名代表,
其中甲宿舍至少选1人,则一共有多少种不同的选法? ( )
(A) C![]() ·C
·C![]()
(B) C![]() ·C
·C![]()
(C) C![]() ·C
·C![]() ·C
·C![]()
(D) C![]() ·C
·C![]() +C
+C![]() ·C
·C![]() +C
+C![]()
10. 设在抛物线的顶点在原点,其焦点F在y轴上,又抛物线上的点(k, -2)与F点的距
离为4,则k等于:( )
(A) 4 (B) 4或-4
(C) -2 (D) 2或-2
11. 设 z![]() ,z
,z![]() 非零复数,则条件“
非零复数,则条件“![]() ·z
·z![]() i” 是“复数z
i” 是“复数z![]() 、z
、z![]() 所对应的向
所对应的向
量互相垂直”的( )
(A) 充分但不必要条件
(B) 必要但不充分条件
(C) 充分必要条件
(D) 既不充分也不必要条件
12. 在空间四边形的4条边所在的直线中,互相垂直的直线对最多可以有( )
(A) 2对 (B) 3对
(C) 4对 (D) 5对
13. 设等差数列的前4项之和为26,其末4项之和是110,又这个数列的所有的项
之和为187,则这个数列共有多少项? ( )
(A) 11项 (B) 22项
(C) 8项 (D) 项数不能确定
14. 设一个圆锥与一个圆柱的底面半径及高都对应相等,它们的侧面积分别为S![]() 、S
、S![]() ,
,
则必有:( )
(A) S![]() <S
<S![]() (B) S
(B) S![]() =S
=S![]()
(C) S![]() >S
>S![]() (D) 以上三种情况均有可能成立。
(D) 以上三种情况均有可能成立。
15. 已知函数f(x)=|2![]() -1|,a<b<c且f(a)>f(c)>f(b). 则必有( )
-1|,a<b<c且f(a)>f(c)>f(b). 则必有( )
(A) a<0, b<0, c<0 (B) a<0, b≥0, c>0
(C) 2![]() <2
<2![]() (D)
2
(D)
2![]() +2
+2![]() <2
<2
二、填空题
16. 函数 ![]() 的最大值是( )
的最大值是( )
(A) ![]() (B) -
(B) -![]()
(C) -![]() (D)
(D)![]()
17. 已知正三棱锥的侧棱与底面所成的角为30°,则其侧面与底面所成的二面角的大小
为( )
(A) arc ![]() (B) arc
(B) arc ![]()
(C) arc ![]() (D) arc
(D) arc ![]()
18. 圆ρ=2cosθ与圆ρ=2cosθ+4sinθ的圆心之间距离为( )
19. 设集合 An=|x|2![]() <x<2
<x<2![]() 且x=7m+1,m、n∈N,
且x=7m+1,m、n∈N,
则 A![]() 中各元素之和等于( )
中各元素之和等于( )
三、解答题
20. 已知 ctgθ=-![]() 且 -
且 -![]() <θ<
<θ<![]() , 求 sin2θ的值。( )
, 求 sin2θ的值。( )
(A) ![]() (B) -
(B) -![]()
(C) -![]() (D)
(D) ![]()
[解析]
21. 计算复数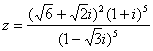 ( )
( )
(A) -1+i (B) -1-i
(C) 1-i (D) 1+i
并求argz. ( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[解析]
22. 设公比的绝对值小于1的无穷等比数列:1,x(1-x), x![]() (1-x)
(1-x) ![]() , ……,
, ……,
x![]() (1-x)
(1-x) ![]() .……各项的和S>1,试确定实数x的取值范围( )。
.……各项的和S>1,试确定实数x的取值范围( )。
(A) x<0 (B) 0<x<1
(C) x<0或x>1 (D) x>1
|
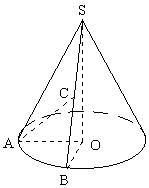
23.设SA、SB是圆锥SO的两条母线,O是底面圆心,底面半径为 10厘米,C是SB上一点。
(1) 求证:AC与平面SOB不垂直, |
[解析]
(2) 若∠AOB=60°,C是SB的中点,AC与底面成45°角,则这圆锥的体积是( )
(A) ![]() (B)
(B)
![]()
(D) ![]() (C)
(C) ![]()
[解析]
24. 甲工厂去年上交利税40万元,今后5年内计划每年平均增长10%,乙工厂去年上交利税比甲工厂少,今后5年内计划每年平均增长20%,这样从今年起,二年乙工厂上交利税就能超过甲工厂,但是要到第三年末,才能使从今年开始的三年内上交的总利税不少于甲工厂,求乙工厂去年大约上交利税多少万元? (只取到整数万元) ( $W*34$ )
[解析]
25. 设f(x)是定义在(-∞,+∞)上以2为周期的周期函数,且f(x)是偶函数在区间
[2,3]上,f(x)=-2(x-3)![]() +4
+4
(1) 求x∈[1,2]时,f(x)的解析表达式。( )
(A) y=2(x-1)![]() +4
(B) y=-2(x-1)
+4
(B) y=-2(x-1)![]() +4
+4
(C) y=2(x-1)![]() -4
(D) y=-2(x-1)
-4
(D) y=-2(x-1)![]() -4
-4
[解析]
(2) 若矩形ABCD的两个顶点A、B在x轴上,C、D在函数y=f(x)(0≤x≤2)
的图象上,求这个矩形面积的最大值是: ( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
[解析]
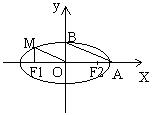
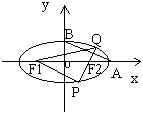
26. 从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点 F![]() ,且其长轴端点A及
,且其长轴端点A及
短轴端点B的连线AB平行于OM。
(1) 则椭圆的离心率是: ( )
|
(A) (C) |
[解析]
(2) 若Q是椭圆上任意一点,F![]() 是右焦点,求 ∠F
是右焦点,求 ∠F![]() QF
QF![]() 的取值范围: ( )
的取值范围: ( )
|
(A) (0, (C) (0, |
[解析]
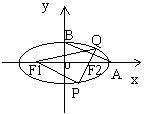
(3) 当 QF![]() ⊥AB 时,延长 QF
⊥AB 时,延长 QF![]() 与椭圆交于另一点P,若 △F
与椭圆交于另一点P,若 △F![]() PQ 的面积为
PQ 的面积为
20![]() .(Q是椭圆上的点),此时椭圆的方程: ( )
.(Q是椭圆上的点),此时椭圆的方程: ( )
|
(A) (C) |
[解析]
参 考 答 案
一、 1. B 2. A 3. C 4. A 5. A
6. B 7. C 8. C 9. D 10. B
11. A 12. B 13. A 14. D 15. D
二、16. D 17. B 18. 2 19. 891
三、20. C [解析]
∴ 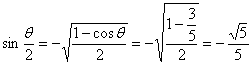
sin2θ=2sinθ.cosθ=2·(-![]() )·
)·![]() =-
=-![]()
21. B; D [解析]
z=-l-i ∴ argz=![]()
22. B
23. (1)[解析] 证明:假设AC⊥平面SOB 那么由SO⊥底面AOB
得平面SOB⊥底面AOB,其交线为BO 作AD⊥OB于D
则AD⊥平面SOB 又AC⊥平面SOB 故AD∥AC
这与“AD与AC相交于A点”矛盾,
因此原假设不对,即AC与平面SOB不垂直,
(2) A [解析]
作CK⊥OB于K ![]()
![]() (立方厘米)
(立方厘米)
24. ( 34 ) [解析]
设乙工厂去年大约上交利税x万元,那么,依条件
x(1+20%)![]() >40(1+10%)
>40(1+10%)![]()
即可得:![]() <x<35
<x<35
x(1+20%)![]() ≤40(1+10%)
≤40(1+10%)
![]() <
<![]()
依条件只取 x=34,
![]() ≥
≥![]()
故乙工厂去年大约上交利税34万元。
25. (1) B
[解析] f(x)=f(x-4)=-2[(x-4)+3]![]() +4
+4
=-2(x-1)![]() +4 (1≤x≤2)
+4 (1≤x≤2)
(2) A
[解析] 矩形ABCD的面积 S=|AB|·|BC| =2t(-2t![]() +4)=4t(2-t
+4)=4t(2-t![]() )
)
当![]() ∈[0.1]即
∈[0.1]即 ![]() 时,矩形ABCD的面积S有最大值
时,矩形ABCD的面积S有最大值![]()
26. (1) C [解析]
椭圆的离心率 ![]()
(2) B [解析]
∠F![]() QF
QF![]() ∈ [0,
∈ [0,![]() ]
]
(3) A [解析] 直线PQ方程为:![]() 即
即 ![]()
代入:x![]() +2y
+2y![]() =2c
=2c![]() 之中,得:x
之中,得:x![]() +4(x
+4(x![]() -2cx+c
-2cx+c![]() )=2c
)=2c![]()
即5x![]() -8cx+2c
-8cx+2c![]() =0
=0
|PQ|![]()
![]()
S△F![]() PQ=
PQ=![]() 且 c>0 因此所求方程为:
且 c>0 因此所求方程为:![]()