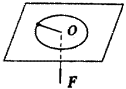
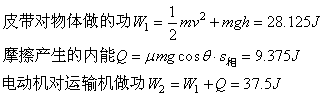第七章 机械能

一、基本概念

1、做功的两个必备因素是力和在力方向上的位移．而往往某些力与物体的位移不在同一直线上，这时应注意这些力在位移方向上有无分力，确定这些力是否做功．

2、应用公式W＝Fscosα计算时，应明确是哪个力或哪些力做功、做什么功，同时还应注意：

(1)F必须是整个过程中大小、方向均不变的恒力，与物体运动轨迹和性质无关．当物体做曲线运动而力的方向总在物体速度的方向上，大小不变，式中α应为0，而s是物体通过的路程．

(2)公式中α是F、s之间夹角，在具体问题中可灵活应用矢量的分解；一般来说，物体作直线运动时，可将F沿s方向分解；物体作曲线运动时，应将s沿F方向分解，

(3)功是标量，但有正负，其正负特性由F与s的夹角α的取值范围反映出来．但必须注意，功的正负不表示方向，也不表示大小，其意义是表示物体与外界的能量转换．

(4)本公式只是计算功的一种方法，今后还会学到计算功的另外一些方法，尤其是变力做功问题，决不能用本公式计算，那时应灵活巧妙地应用不同方法，思维不能僵化．

3、公式P=W/t求得的是功率的平均值。P=Fvcosα求得的是功率的瞬时值。当物体做匀速运动时，平均值与瞬时值相等。

4、P＝Fvcosα中的α为F与v的夹角，计算时一般情况下当物体做直线运动时，可将F沿v方向与垂直v方向上分解，若物体作曲线运动时可将v沿F及垂直F的两个方向分解．

5、P＝W/t提供了机械以额定功率做功而物体受变力作用时计算功的一种方法．

6、功和能的关系应从以下方面理解：不论什么形式的能，只要能量发生了转化，则一定有力做功；能量转化了多少，力就做了多少功．反之，只要有力做功，则一定发生了能量转化；力做了多少功，能量就转化了多少．所以功是能量转化的量度，但决不是能的量度．

7、功与能是不同的概念，功是一个过程的量，而能是状态量。正是力在过程中做了功，才使始末状态的能量不同，即能量的转化．说功转化为能是错误的．

8、“运动的物体具有的能叫动能”这句话是错误的．因为运动的物体除了动能外还有势能．

9、关于重力势能，应明确：(1)重力势能的系统性，即重力势能是物体和地球共有的，而不是物体独有的，“物体的重力势能”是一种不够严谨的习惯说法．(2)重力势能的相对性，势能的量值与零势能参考平面的选取有关．E_p=mgh中的h是物体到参考平面的竖直高度．通常取地面为参考平面．解题时也可视问题的方便随意选取参考平面．(3)重力势能的变化与参考平面的选取无关，只与物体的始末位置有关．

10、重力做功的特点：(1)与路径无关，只由重力和物体始、末位置高度差决定．(2)重力做功一定等于重力势能的改变．即W_G=E_p1-E_p2，当重力做正功时，重力势能减少；当重力做负功时，重力势能增加。

11、关于动能定理，要注意动能定理的表达式的等号左边是且仅是所有外力的功，等号右边是且仅是物体动能的改变量。在列动能定理方程时，不要考虑势能及势能的变化。

12、关于机械能守恒定律应明确：

(1)定律成立的条件是“只有重力做功或弹力做功”，不是“只有重力作用或弹力作用”．有其它力作用，但其它力不做功，而只有重力做功或弹力做功时，机械能仍守恒．

(2)定律表示的是任一时刻、任一状态下物体机械能总量保持不变，故可以在整个过程中任取两个状态写出方程求解．

(3)定律的表达式除了写成E_p1+E_p2=E_k1+E_k2外，还可写成ΔE_p=-ΔE_k，即在任一机械能守恒的过程中，重力势能的减少(增加)一定等于动能的增加(减少)。利用ΔE_p=-ΔE_k进行计算有时会显得简明．

13、应用机械能守恒定律解题时，只要考虑始末态下的机械能，无须顾及中间过程运动情况的细节。因此，对于运动过程复杂、受变力作用、作曲线运动等不能直接应用牛顿运动定律处理的问题，利用机械能守恒律会带来方便。

14、应用机械能守恒定律解题的一般步骤：

(1)认真审题，确定研究对象；

(2)对研究对象进行受力分析和运动过程、状态的分析，弄清整个过程中各力做功的情况，确认是否符合机械能守恒的条件；

(3)确定一个过程、两个状态(始末)，选取零势能参考平面，确定始末状态的动能、势能值或这个过程中ΔE_p和ΔE_k的值；

(4)利用机械能守恒定律列方程，必要时还要根据其它力学知识列出联立方程；

(5)统一单位求解．

解题的关键是准确找出始、末状态的动能和势能的值，尤其是势能值的确定．

二、恒力做功与变力做功问题

1、恒力做功

求解恒力功的方法一般是用功的定义式W=Fscosα，需要特别注意：

（1）位移s的含义：是力直接作用的物体对地的位移。当力在物体上的作用位置不变时，s就是力作用的那个质点的位移；当力在物体上的作用位置不断改变时，s应是物体的位移。如：一个不能视为质点的物体受到滑动摩擦力作用时，摩擦力的作用点时时变化，此时s就不是摩擦力作用点的位移，而是物体的位移。

例 如图示，质量为m、初速为v₀的小木块，在桌面上滑动。动摩擦因数为μ，求木块停止滑动前摩擦力对木块和桌面所做的功。

解 对木块：W₁=-fs=-μmg·v₀²/（2gμ）=-mv₀²/2

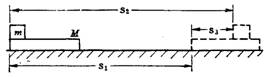对桌面：W₂=0

例 如图示，质量为m、初速为v₀的小木块，在一块质量为M的木板上滑动，板放在光滑水平桌面上，求木块和板相对静止前，摩擦力对木块和木板所做的功。

解 据动量守恒mv₀=（m+M）v得　　 

W₁=-fs₂=-μmg·M（M+2m）v₀²/（M+m）²2gμ=-Mm(M+2m)v₀²/2（M+m）²

W₂=fs₁=Mm²v₀²/2（M+m）²gμ

（2）一对相互作用力所做功之和不一定为零

如：人竖直向上跳起，地面对人的作用力对人做正功，人对地而不做功（地球位移视为零），总功为正；

一对静摩擦力，位移值一定相同，总功必为零；

一对滑动摩擦力，做功时必然发热，系统内能增加，总功必为负。转化为内能值为　　　　

2、判断做功正负的方法

（1）从力与位移或速度方向的关系进行判断。

如：“子弹打木块”问题，摩擦力对子弹做负功，对木块做正功。

例 如图所示，质量为M的木块静止在光滑水平面上，质量为m的子弹以水平速度射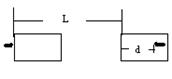中与木块一起以速度v运动，已知当子弹相对木块静止时，木块前进距离为L，子弹进入木块的深度为d，若木块对子弹的阻力F恒定，那么下列关系式中正确的是（　　）、、

A、　　　　　　　  B、

C、　D、

（2）从能量的增减进行判断

例 如图示，在质量不计、长度为L的直杆一端和中点分别固定一个质量都是m的小球A和B，试判断当杆从水平位置无摩擦地转到竖直位置的过程中，杆对A、B球做功的正负。

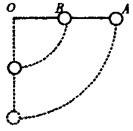解 A、B两球组成的系统的机械能守恒，由机械能守恒定律：

由于两球在同一杆上，角速度相等，故

解之得：，

与A、B球自由下落时的速度比较，，

可见，，故杆对A球做正功，对B球做负功。

3、变力做功

大小或方向变化的力所做的功，一般不能用功的公式W=Fscosα去求解．需变换思维方式，独辟蹊径求解。

(1)用功率定义式求解

将功率的定义式P=W/t变形，得W=Pt。在求解交通工具牵引力做功问题时经常用到此公式。

例 质量为m的汽车在平直公路上以初速度v₀开始匀加速行驶，经时间t前进距离s后，速度达最大值v_m，设在这段过程中发动机的功率恒为P，汽车所受阻力恒为f，则在这段时间内发动机所做的功为：

A、Pt　　　　　 B、fv_Mt

C、fs+mv_m²/2　　 D、mv_m²/2-mv₀²/2+fs

（答案：ABD）

(2)用动能定理求解变力做功

求解某个变力所做的功，可以利用动能定理，通过动能改变量和其余力做功情况来确定。

例 如图所示，把一小球系在轻绳的一端，轻绳的另一端穿过光滑木板的小孔，且受到竖直向下的拉力作用．当拉力为F时，小球做匀速圆周运动的轨道半径为R．当拉力逐渐增至4F时，小球匀速圆周运动的轨道半径为R／2．在此过程中，拉力对小球做了多少功?

解 此题中的F是一个大小变化的力，故我们不能直接用功的公式求解拉力的功．

根据F=mv²／R，我们可分别求得前、后两个状态小球的动能，这两状态动能之差就是拉力所做的功．

由F=mv₁²／R　 4F=mv₂²／0.5R

得W_F=mv₂²／2-mv₁²／2=FR/2

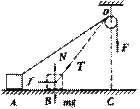
例 如图，用F＝20N的恒力拉跨过定滑轮的细绳的一端，使质量为10kg的物体从A点由静止沿水平面运动．当它运动到B点时，速度为3m／s．设OC＝4m，BC＝3m，AC＝9.6m，求物体克服摩擦力做的功．

解 作出物体在运动过程中的受力图。其中绳的拉力T大小不变，但方向时刻改变．N随T方向的变化而变化(此力不做功)．f随正压力N的变化而变化．因此对物体来说，存在着两个变力做功的问题．但绳拉力T做的功，在数值上应等于向下恒力F做的功．F的大小已知，F移动的距离应为OA、OB两段绳长之差．

由动能定理 W_F+W_f=ΔE_k　得：

W_f＝-63(J)

即物体克服摩擦力做了63J耳的功．

(3)用图象法求解变力做功

如果能知道变力F随位移s变化的关系，我们可以先作出F-s关系图象，并利用这个图象求变力所做的功．

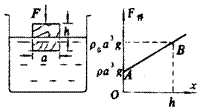[例]如图，密度为ρ，边长为a的正立方体木块漂浮在水面上(水的密度为ρ₀)．现用力将木块按入水中，直到木块上表面刚浸没，此过程浮力做了多少功?

解 未用力按木块时，木块处于二力平衡状态

F_浮=mg　即ρ₀ga²（a-h）=ρga³

并可求得：h=a（ρ₀-ρ）/ρ₀（h为木块在水面上的高度）

在用力按木块到木块上表面刚浸没，木块受的浮力逐渐增大，上表面刚浸没时，浮力达到最大值：F’_浮=ρ₀ga³

以开始位量为向下位移x的起点，浮力可表示为：

F_浮=ρga³+ρ₀ga²x

根据这一关系式，我们可作出F_浮-x图象(如图右所示)．在此图象中，梯形OhBA所包围的“面积”即为浮力在此过程所做的功。

W=（ρ₀ga³+ρga³）h/2=ga³h（ρ₀+ρ）/2

这里的“面积”为什么就是变力所做的功?大家可结合匀变速运动的速度图象中的“面积”表示位移来加以理解．即使F-x关系是二次函数的关系，它的图象是一条曲线，这个“面积”仍是变力在相应过程中所做的功．

三、重力功率与交通工具起动问题

1、重力的功率

（1）自由落体过程中重力的功率

（2）平抛运动中重力的功率

（3）沿斜面滑行的物体的重力的功率

例 质量为m的物体，由静止开始沿倾角为θ的光滑斜面下滑，求前3s内、第3s内、第3s末重力做功的功率。

解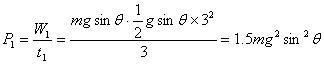

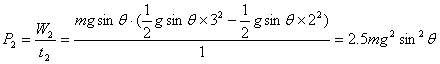
2、交通工具起动时的牵引力及功率

汽车等交通工具的起动方式有两种：一是以恒定功率起动，二是汽车以恒定的牵引力起动，具体分析如下：

（1）输出功率不变时的运动

由于牵引力F＝P／v，随着速度v的增大，牵引力F减小，则加速度a=（F-f）/m减小，但因a与v同向，汽车的速度v不断增大，F减小，a减小，直至a=0时，汽车作匀速运动，此时速度为最大值v_m＝P/F=P/f，在此之前，由牛顿第二定律得：（P/v）-f=ma，可知任一速度值均有与之相对应的一个确定的加速度值．由于汽车做变加速运动，所以不能用匀变速直线运动的公式求解，也不能对全过程应用牛顿第二定律，但动能定理是适用的，力和加速度瞬时对应关系也成立，因此解题时通常是对某一过程列动能定理方程，对某一瞬时列牛顿第二定律方程．

例 辆机车的质量为750T，沿平直轨道由静止开始运动．它以额定功率在5分钟内驶过2.5km，并达到10m／s的最大速度．求：(1)机车发动机的额定功率P和机车与轨道间的摩擦因数μ分别是多少?(2)当机车速度为5m／s时的加速度多大(g取10m／s²)

解 图所示，设机车在A处起动，因功率不变，故随着速度的增大，牵引力减小，加速度减小，机车做变加速运动．当牵引力减小到F=f的B处时，速度达到最大值v_m，以后机车做匀速运动．

(1)由动能定理得：Pt-μmgs=mv_m²/2　　　 ①

在B处：F=f=μmg，故有P=Fv=μmgv_m　　 ②

将②式代人①式、并代入数据可得：

μ=0.01

再将μ值代入②式得：

P=7.5×10⁵J

(2)设此时牵引力为F’,则

F’=P/v’=7.5×10⁵／5=1.5×10⁵N

再由F’-f=ma得

a=(F’-f)/m=0.1m／s²

例 出功率保持10kw的起重机起吊500kg的重物，当货物升高到2m时速度达到最大值，此最大速度是多少?此过程用了多长时间?(g取10m／s²)

解 重机以恒定的功率吊起重物的过程是加速度不断减小、速度不断增大的过程.当货物的速度达到最大时，起重机的牵引力与货物的重力相平衡，即：

F=mg=5×10³N，v_m＝P／F=2m／s．

求解这一段运动时间不能用匀变速运动的公式，我们可以货物为研究对象运用动能定理求解：

Pt-W_G=mv²/2,　t=(mv²/2+mgh)/P=1.1s

(2)牵引力不变时的运动

汽车以恒定的牵引力起动，则汽车开始一段时间作匀加速运动，由v=at及P=Fv=Fat可知，随时间的延长汽车的功率越来越大，直到达到其最大功率时，输出功率不能再增大，但此时由于牵引力仍大于阻力，汽车仍加速，则因受最大功率的制约，牵引力必须减小，汽车做加速度越来越小的匀加速运动，直至a=0时做匀速运动，故此种情形下，汽车前一阶段做匀加速运动，后一阶段做变加速运动。在汽车做匀加速运动阶段中, 我们既可以运用功的公式、动能定理来求解，也可以运用牛顿运动定律来求解．对变加速运动阶段,则必须用第(1)点的方法求解.

例 车的质量为m，它在运动中受到的阻力f恒定不变。汽车发动机的额定功率为P，求：(1)汽车在作匀加速运动时的长大速度是多少?(2)汽车从静止出发作加速度为a的匀加速运动的时间不应超过多少?

解 车受到的阻力一定，且又做的是匀加速运动，所以它受到的牵引力也是一定的．

F-f=ma

随着速度的增加,汽车的输出功率也在不断增大．当输出功率达到额定功率时，这时汽车行驶的速度不允许再增加了．此时有：

v_m=P/F=P/(ma+f)

再根据运动学公式，可求出这段过程所需时间：

t=v_m/a=P/[(ma+f)a]

四、动能定理

1、灵活选取适当过程，运用动能定理

例 量过为4kg的铅球，从离沙坑1.8m的高处自由落下.铅球落进沙坑后陷入0.2m深而停止运动，求沙坑对铅球的平均阻力(g取10m／²).

解 铅球在前一段作自由落体运动，后一段作匀减速运动．对前一段可用机械能守恒求解，后一段可用动能定理求解．但如果我们把开始下落到最终停止看成一个过程，运用动能定理列式，将很快得到结果：

由W=ΔE_k　可得：mg（h+s）-fs=0-0=0

f=（h+s）mg/s=（1.8+0.2）×4×10／0.2=400N

此题我们用动能定理列式时，把两段过程处理成一个过程，求解就便捷得多了．

2、结合隔离法，运用动能定理

例 质量为M的列车，沿平直轨道匀速前进，质量为m的末节车厢中途脱钩，当司机发觉时，机车已行驶L距离，于是他立即关闭油门，撤去牵引力。设车运动的阻力与重力成正比，机车的牵引力为定值，当列车的两部分都停止运动时，它们的距离是多少?

 解 此题牵涉机车和车厢这两个研究对象，它们又分别经历着不同的变速运动过程．如果从动力学、运动学角度去分析求解将非常麻烦．我们运用隔离法针对每一个研究对象运动的全过程分析其受力，画出其运动的示意图如图所示，并分别列出它们动能定理的表达式：

未脱钩时，整列车匀速前进，有：F=KMg　　(1)

脱钩后，两车分别作加速、减速运动

对机车：FL-K（M-m）gs₁=0-（M-m）v₀²/2　 (2)

对车厢：-Kmgs₂=0-mv₀²/2　　　　　　　　 (3)

将(1)代入(2)后再将等式两边分别与(3)相除，化简，得：

Δs=s₁-s₂=ML/（M-m）

3、结合运动分解，运用动能定理

例 如图所示，某人通过过一根跨过定滑轮的轻绳提升一个质量为m的重物，开始时人在滑轮的正下方，绳下端A点离滑轮的距离为H。人由静止拉着绳向右移动，当绳下端到B点位置时，人的速度为v，绳与水平面夹角为θ。问在这个过程中，人对重物做了多少功?

解 人移动时对绳的拉力不是恒力，重物不是做匀速运动也不是作匀变速运动，故无法用W=Fscosθ求对重物作的功，需从动能定理的角度来分析求解．

当绳下端由A点移到B点时，重物上升的高度为：

重力做功的数值为：

当绳在B点实际水平速度为v时，v可以分解为沿绳斜向下的分速度v₁和绕定滑轮逆时针转动的分速度v₂，其中沿绳斜向下的分速度v₁和5重物上升速度的大小是一致的，从图中可看出：v₁=vcosθ

以重物为研究对象，根据动能定理得：

4、动能定理与牛顿运动定律的比较

用牛顿运动定律解题涉及到的有关物理量比较多，如F、a、m、v、s、t等．对运动过程的细节变化也要掌握得比较充分，才可列式求解。而运用动能定理解题涉及到的物理量只有F、s、m、v．它对运动过程的细节及其变化也不要求了解，只需考虑始末两状态的动能和外力做的功，它还可把不同运动过程合并成一个全过程来处理，使解题过程简便．当然，如果题目中要求了解加速度a、运动时间t等细节，那就需要从动力学、运动学的角度去分析，不能直接求解了。

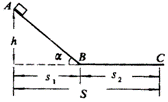例 如图所示，小滑块从斜面顶点4由静止滑至水平部分C点而停止．已知斜面高为h，滑块运动的整个水平距离为s．求小滑块与接触面间的动摩擦因数(设滑块与各部分的动摩擦因数相同)．

解 滑块从A点滑到C点，只有重力和摩擦力做功，设滑块质量为m，动摩擦因数为μ，斜面倾角为α，斜面底边长s₁，水平部分长s₂，由动能定理得：

得μ=h/s

由此题可见，用动能定理求解，回避了加速度a，不必考虑细节，解题过程简单很多．

五、重力做功与重力势能的改变

1、物体受到重力作用具有重力势能。它的表达式E_p＝mgh，适用于g不变的情况。式中h是相对于选定的零势能面的高度，所以重力势能和功、动能一样具有相对性。重力势能也是标量，有正、负、零之分。重力势能等于零，并不意味着物体不具有重力势能，零值势能比负势能大。因此，在比较势能大小时，既要选取同一参考面，又要注意它的符号，这跟功大小的比较是不一样的。

2、重力做功一定改变物体的重力势能，这是又一种重要的功能关系。在一个过程中，重力做多少功，重力势能就减少多少，克服重力做多少功，重力势能就增加多少，而跟零势能面的选取无关，跟物体做什么运动，是否有其它力做功以及物体动能是否变化等也无关，这是要特别注意的。

例 物体从A运动到B点的过程中，重力做功8J，推力做功2J，物体克服阻力做功10J。则：

A、物体重力势能一定减少8J　　 B、物体机械能一定减少10J

C、合力功为零　　　　　　　　 D、重力做功一定不改变物体的动能

（答案）AC

六、机械能守恒定律的应用

系统内力做功问题

凡符合“只有重力做功，其它力均不做功”这一条件的问题，用机械能守恒定律来求解是十分方便的。因为它只涉及到研究对象(某一物体或某一物体系统)的始末两状态的机械能，而不考虑运动过程的任何细节，也不考虑做功的数值，列式和求解都很便捷．

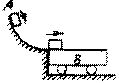对于单一物体，我们很容易判断它是否满足机械能守恒的条件对于某一系统来说，用隔离法考察系统内每一个物体，它们可能不符合机械能守恒的条件。但对整体，除重力外，无其它外力做功，且内力做功的代数和为零，则该系统的机械能也是守恒的。如图示，A和B在运动中除了重力做功外，绳子拉力对它们都做功，因而在A上升和B下降过程中，A和B各自的机械能不守恒，但如果把它们看成一个整体，则绳子拉力是它们之间相互作用的内力，拉力对A做正功的数值和拉力对B做负功的数值相等，就整体而言，内力不做功，故整个系统机械能守恒。

有些问题中，系统所受其它外力不做功，但系统内力做功的代数和不为零，则该系统的机械能就不守恒。如图示，滑块A滑上小车B粗糙的上表面后，A、B之间相互作用的内力（摩擦力）做功的代数和不为零，即使地面光滑，A、B系统的机械能也是不守恒的。

例 如图所示，在光滑的水平面上放有一质量为m、高为a的立方块．一根轻杆长4a，下端用铰链固定在地面上，上端固定一质量也为m的重球．开始杆与水平面成53°角静止，杆与木块无摩擦．释放后，当杆与水平面成30°角时，木块速度多大?

解 此题球与木块的运动过程复杂，有关力做功的情况又不清楚，放无法从动力学、动能定理求解．我们可把球和木块看成一个系统，对此系统来说，只有小球重力做功，内力做功代数和为零，系统的机械能是守恒的(杆的质量不计，其能量也不考虑)。

由机械能守恒定律，可得：

　　（1）

从图中看出，木块实际运动速度v_木可分解为沿杆向上的速度v₁和垂直于杆的速度v₂，且：

v₂=v_木sin30°＝v_木/2

小球的速度也垂直于杆的，它与v₂的比值等于转动半径之比：

，v_球=2v₂=v_木　　　（2）

把(2)式代入(1)即可得

七、动量守恒和机械能守恒

动量守恒和机械能守恒是力学中两个重要的守恒定律，它们有完全不同的守恒内容和各自严格的成立条件，必须学会区别和判定。

一物体被匀速提起，其动量守恒，动能也守恒，但重力势能增加，机械能不守恒，这是因为有重力以外的拉力做正功的原因。

单摆运动，显然动量不守恒，动能也不守恒，但绳拉力不做功，运动过程只有重力做功，所以机械能守恒。

做抛体运动的物体如果有受到空气阻力作用，物体的动量、动能、机械能都不守恒。

例 如图示，甲、丙是具有四分之一圆弧的光滑槽，乙是粗糙水平槽。三者相触置放于光滑水平面上，能让小球在其上平顺滑过。现让小球从高处落下恰能切入甲槽。下列说法正确的是：

A、球在甲槽上滑行时，取球和甲为系统，动量不守恒，系统机械能守恒。

B、球滑上乙后，取球乙、丙为系统，系统水平方向动量守恒，机械能不守恒。

C、球滑上丙后，取球、丙为系统，机械能守恒，水平方向的动量守恒。

D、取甲、乙、丙为系统，机械能守恒，动量也守恒。

（答案）ABC

例 如图，摆球质量m＝0.1kg，摆长L＝0.1m，球与水平面接触而无压力。两侧等远处有正对挡板，相距2m。另有质量M＝m的小滑块与水平面间摩擦因数为0.25，从左挡板处以初速的向小球方向运动。设滑块与小球，滑块与挡板的每次碰撞系统均无机械能损失。滑块静止前小球在竖直面内绕O点完成10次完整的圆周运动，求v₀的最小值。(g取10m／s²)

解 取滑块和小球为一系统，碰撞前后水平方向动量守恒。因M＝m，碰撞无能量损失，所以碰后二者交换速度，即滑块停于中点，小球作圆周运动。当小球反碰滑块时，小球停止，滑块继续向右，碰挡板后等值反向运动，重复上述过程。此外，滑块滑行过程克服阻力做功，动能减少，因此，小球圆周运动的速度也越来越小。第10次圆周运动小球在最高点的速率v₂应为＝1m/s。根据机械能守恒定律，这时小球在最低点速度v₁为m/s，这也就是滑块在小球完成10次圆周运动后具有的最小速度。容易推算，这之前滑块已来回滑行19米的路程，根据动能定理，设滑块的最小初速度为v₀，应有：

　　　　得v₀＝10m/s

八、一道含有弹簧的系统的机械能守恒问题

机械能等于动能与势能的代数和，而势能包括重力势能与弹性势能，即E＝E_k+E_p+E_p’，我们在学习过程中遇到的大多是关于动能与重力势能的问题。下面则是一道含有弹簧的机械能守恒问题，现在我们结合机械能解题的基本方法对该例题进行分析。

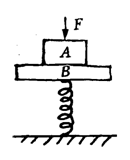例 如图，竖直向下的力F作用于质量为m₁的物体A上，物体A置于质量为m₂的物体B上，B与原长为L的直立于水平地面上的轻弹簧上端相连，平衡时弹簧的压缩量为x。现将F撤去．物体AB向上运动，且物体A向上运动达到最高点时离地面高度为h，求：①弹簧恢复原长时物体A的速度；⑨弹簧弹性势能的最大值。

[分析]（一）判断机械能是否守恒：(此类问题应首先考虑能量方法，其次才考虑其它方法)

在整个过程中(F撤消后)，只有重力及弹簧弹力对物体做功，所以物体AB与弹簧组成的系统机械能守恒。

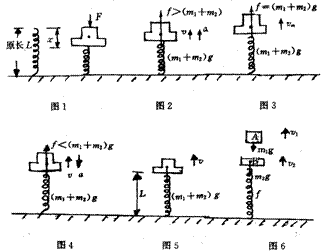（二）设想物理图景，分析各图景中的受力、运动及能量转化情况：(以下物理图景与分析步骤对应)

1、初始状态：物体AB处于平衡状态，对AB整体受力分析得：f=kx=F+（m₁+m₂）g。

2、力F撤消后，由于f>（m₁+m₂）g，物体AB受到的合力方向向上，AB将开始向上运动。因此弹簧压缩量x减小；弹力f减小F_合=f-（m₁+m₂）g也随之减小，加速度a也减小，所以物体AB将向上做加速度逐渐减小的变加速运动。该过程中，弹簧弹性势能转化为物体AB的动能与重力势能。

3、当f=（m₁+m₂）g时，F_合=0，即a=0，物体AB向上的速度达到最大值v_max。

4、物体AB继续向上运动，弹力f=kx继续减小，此时f<（m₁+m₂）g，AB受到合力方向向下，大小F_合=（m₁+m₂）g-f，由于f减小，F_合增大，a增大，因此物体AB向上做加速度增大的减速运动，速度逐渐减小。该过程仍为弹簧弹性势能转化为AB的动能与重力势能。

5、当弹簧恢复原长时，f=0，物体AB此刻有相同向上速度v。

6、物体AB继续向上运动，物体A受重力m₁g，而B由于弹簧被拉伸还受到向下的弹簧弹力f，因此弹簧恢复原长后，物体A与B脱离。物体A做竖直上抛运动，机械能守恒；物体B由于弹簧作用将做上下往复运动，B与弹簧组成的系统机械能也守恒。

以上对整个运动过程作了较详细分析后，解题思路就清晰了。

解 ①弹簧恢复原长后，(图6)向上做上抛运动，机械能守恒，即：m₁gL+m₁v²/2=m₁gh

所以：

②弹簧弹性势能E_p’最大，(即图1中弹性势能E_p’)当力F撤消后，图l至图5中，弹性势能转化为AB的动能与重力势能，至弹簧恢复原长，弹性势能为0，此过程系统机械守恒：

E_pmax’=（m₁+m₂）v²/2+（m₁+m₂）gx

=（m₁+m₂）g(h-L-x)

九、功能关系和能量守恒

1、能的转化和守恒守律：能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为别的形式，或者由一个物体转移到别的物体，而在这种转化和转移中保持能的总量不变。

2、功能关系：做功的过程就是能的转化的过程，做了多少功，就有某种形式的能转化成等量的其它形式的能，即功是能的转化的量度(功不是能，也不是能量大小的量度)。重力做功是重力势能变化的量度；合力做功是动能变化的量度。如果只有重力做功，减少的重力势能等量地转化为动能，机械能是守恒的。在实际问题中，常常遇到除重力做功以外，还有牵引力、阻力等其它外力做功的情况。这时，物体的机械能就发生变化。如果重力以外的力做功的代数和是正的．机械能增加；重力以外的力做功的代数和是负的，机械能减少。重力以外的力做功是机械能变化的量度，即：重力以外的其余力做功等于机械能的改变。

功能关系跟动能定理是一致的。某些问题，物体机械能的变化是显而易见的，这时利用功能关系求其它力做功就十分方便。

例 如图所示，有底面积为S的蓄水池，内蓄半池水，池深H。现在岸上用抽水机将水抽上，设水从抽水机管中以恒定速率v流出，水密度为ρ，求抽水机抽完水所做的功。

解 显然，研究对象是半池水，其质量m＝SHρ/2。可假设初态机械能为零。抽上地面后其机械能应为。这一机械能的增量即等于抽水机所做的功。

3、功和能是两个不同概念的物理量。功是过程物理量，能是状态物理量。功能关系揭示的是能量状态的改变可以通过做功的过程来实现，并用做功的多少来量度。能的转化和守恒定律揭示的是不同形式能量之间的等量转化或转移。应用功能关系和能的转化和守恒定律解题时，一定要区别功和能，不要混同起来。

例 一物体在电动机牵引下沿斜面向下运动，在一段过程中，牵引力做功8kJ，重力做功10kJ，物体克服摩擦力做功12kJ。则：

A、重力势能减少10kJ　　 B、故动能增加6kJ

C、机械能减少4kJ　　　　D、内能增加12kJ

（答案）ABCD

十、综合应用

单个物体：动量定理（涉及时间）、动能定理（涉及位移）

相互作用的两个物体：动量守恒定律（碰撞等问题）、能量守恒定律（有相对位移）

例 在光滑水平面上，静放着质量为M的木块。若木块固定，质量为m的子弹以水平速度射击木块，恰好穿透。若木块可自由移动，该子弹以相同速度射击木块，则射入的深度等于多少?(设木块厚度为d，两次射击，子弹在木块中所受阻力不变。)

解　第一次

第二次：

　　　　　　　　　　　　　　　　　　　　　

　　　　∴

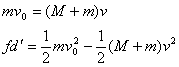
十、关于传送带问题

传送带类分水平、倾斜两种：按转向分顺时针、逆时针转两种。

（1）受力和运动分析：

受力分析中的摩擦力突变（大小、方向）——发生在V_物与V_传相同的时刻；运动分析中的速度变化——相对运动方向和对地速度变化。分析关键是：一是 V_物、V_带的大小与方向；二是mgsinθ与f的大小与方向。

(2)传送带问题中的功能分析

①功能关系：W_F=△E_K+△E_P+Q

②对W_F、Q的正确理解

（a）传送带做的功：W_F=F·S_带　 功率P=F×V_带（F由传送带受力平衡求得）

（b）产生的内能：Q=f·S_相对

（c）如物体无初速，放在水平传送带上，则在整个加速过程中物体获得的动能E_K，因为摩擦而产生的热量Q有如下关系：E_K=Q=

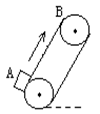例 如图所示，倾角为30°的皮带运输机的皮带始终绷紧，且以恒定速度v＝2.5m/s运动，两轮相距L_AB＝5m，将质量m＝1kg的物体无初速地轻轻放在A处，若物体与皮带间的动摩擦因数μ＝．(取g＝10m/s²）

①物体从A运动到Ｂ,皮带对物体所做的功是多少?

②物体从A运动到B共需多少时间?

③ 在这段时间内电动机对运输机所做的功是多少?

解:第一阶段,物块匀加速运动a=μgcosθ－gsinθ=2.5

,传送带