§2.5几种速度的特殊求法
2.5.1、相关的速度
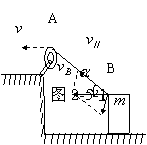 当绳端在做既不沿绳方向,又不垂直于绳方向的运动时,一般要将绳端的运动分解为沿绳方向和垂直于绳方向二个分运动。
当绳端在做既不沿绳方向,又不垂直于绳方向的运动时,一般要将绳端的运动分解为沿绳方向和垂直于绳方向二个分运动。
如图2-5-1所示的情况,绳AB拉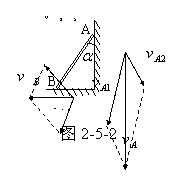 着物体m在水平面上运动,A端以速度v做匀速运动,问m做什么运动?有的同学会将绳的速度v分解成竖直
着物体m在水平面上运动,A端以速度v做匀速运动,问m做什么运动?有的同学会将绳的速度v分解成竖直
分速度vsina和水平分速度vcosa,以为木块的速度![]() (u<v).这是错误的。因为实际上木块并没有一个向上的分速度。应该将绳端B实际上的水平速度
(u<v).这是错误的。因为实际上木块并没有一个向上的分速度。应该将绳端B实际上的水平速度![]() 分解成沿绳方向的分速v∥=
分解成沿绳方向的分速v∥=![]() 和垂直于绳的分速v⊥=
和垂直于绳的分速v⊥=![]() ,v∥使绳子缩短,所以v∥=v,v⊥使绳子围绕滑轮转动。因此
,v∥使绳子缩短,所以v∥=v,v⊥使绳子围绕滑轮转动。因此![]() ,而且
,而且![]() 随着a的增大而越来越大。
随着a的增大而越来越大。
如图2-5-2所示,杆AB沿滑下,A、B二端的速度![]() 和
和![]() 也是二个相关的速度。将
也是二个相关的速度。将![]() 分解成沿杆方向的分速
分解成沿杆方向的分速![]() 和垂直于杆的分速
和垂直于杆的分速![]() 。由于杆的长度不会发生变化,所以
。由于杆的长度不会发生变化,所以![]() ,即
,即![]() ,即
,即
![]()
 2.5.2、两杆交点的运动 两杆的交点同时参与了二杆的运动,而且相对每一根杆还有自己的运动,因而是一种比较复杂的运动。
2.5.2、两杆交点的运动 两杆的交点同时参与了二杆的运动,而且相对每一根杆还有自己的运动,因而是一种比较复杂的运动。
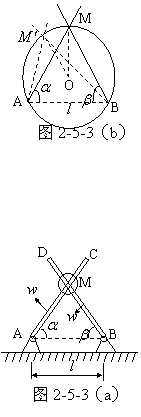
图2-5-3(a)中的AC、BD两杆均以角速度![]() 绕A、B两固定轴在同一竖直面内转动,转动方向如图示。当
绕A、B两固定轴在同一竖直面内转动,转动方向如图示。当
t=0时,![]() 60º,试求t时刻两棒交点M点的速度和加速度。t=0时,△ABM为等边三角形,因此AM=BM=
60º,试求t时刻两棒交点M点的速度和加速度。t=0时,△ABM为等边三角形,因此AM=BM=![]() ,它的外接圆半径R=OM=
,它的外接圆半径R=OM=![]() ,图2-5-3(b)。二杆旋转过程中,
,图2-5-3(b)。二杆旋转过程中,![]() 角增大的角度一直等于
角增大的角度一直等于![]() 角减小的角度,所以M角的大小始终不变(等于60º),因此M点既不能偏向圆内也不能偏向圆外,只能沿着圆周移动,因为∠
角减小的角度,所以M角的大小始终不变(等于60º),因此M点既不能偏向圆内也不能偏向圆外,只能沿着圆周移动,因为∠![]() 和∠
和∠![]() 是对着同一段圆弧(
是对着同一段圆弧(![]() )的圆心角和圆周角,所以∠
)的圆心角和圆周角,所以∠![]() =2∠
=2∠![]() ,即M以2
,即M以2![]() 的角速度绕O点做匀速圆周运动,任意时刻t的速度大小恒为
的角速度绕O点做匀速圆周运动,任意时刻t的速度大小恒为
![]()
向心加速度的大小恒为
![]()
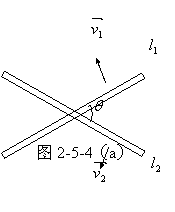
再看图2-5-4(a),一平面内有二根细杆![]() 和
和![]() ,各自以垂直于自己的速度
,各自以垂直于自己的速度![]() 和
和![]() 在该平面内运动,试求交点相对于纸平面的速率及交点相对于每根杆的速率。
在该平面内运动,试求交点相对于纸平面的速率及交点相对于每根杆的速率。
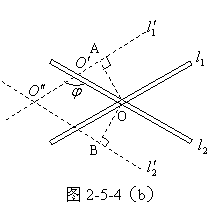
参考图2-5-4(b),经过时间![]() 之后,
之后,![]() 移动到了
移动到了![]() 的位置,
的位置,![]() 移动到了
移动到了![]() 的位置,
的位置,![]() 和
和![]() 的原位置交于
的原位置交于![]() 点,
点,![]() 和
和![]() 交于
交于![]() 点。
点。
![]() =
=![]()
![]()
 在
在![]() 中:
中:
![]()
因为![]() 角和
角和![]() 角互补,所以
角互补,所以
![]()
![]()
因此两杆交点相对于纸平面的速度
![]()
![]()
不难看出,经过![]() 时间后,原交点在
时间后,原交点在![]() 上的位置移动到了A位置,因此交点相对
上的位置移动到了A位置,因此交点相对![]() 的位移就是
的位移就是![]() ,交点相对
,交点相对![]() 的速度就是:
的速度就是:
![]()
=![]()
![]()
用同样的方法可以求出交点相对![]() 的速度
的速度
![]()
因为![]() 可以取得无限小,因此上述讨论与
可以取得无限小,因此上述讨论与![]() 是否为常量无关。如果
是否为常量无关。如果![]() 是变量,上述表达式仍然可以表达二杆交点某一时刻的瞬时速度。
是变量,上述表达式仍然可以表达二杆交点某一时刻的瞬时速度。
如果![]() 和
和![]() 的方向不是与杆垂直,这个问题应该如何解决?读者可以进行进一步的讨论。
的方向不是与杆垂直,这个问题应该如何解决?读者可以进行进一步的讨论。
