第二轮重点突破(3)——平抛运动专题
连城一中 林裕光
当物体初速度水平且仅受重力作用时的运动,被称为平抛运动。其轨迹为抛物线,性质为匀变速运动。平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动这两个分运动。广义地说,当物体所受的合外力恒定且与初速度垂直时,做类平抛运动。
 1、平抛运动基本规律
1、平抛运动基本规律
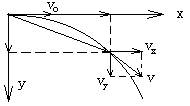
① 速度:![]() ,
,![]()
合速度
![]() 方向 :tanθ=
方向 :tanθ=![]()
②位移x=vot y=![]() 合位移大小:s=
合位移大小:s=![]() 方向:tanα=
方向:tanα=![]()
③时间由y=![]() 得t=
得t=![]() (由下落的高度y决定)
(由下落的高度y决定)
④竖直方向自由落体运动,匀变速直线运动的一切规律在竖直方向上都成立。
应用举例
 (1)方格问题
(1)方格问题
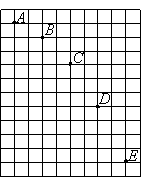
【例1】平抛小球的闪光照片如图。已知方格边长a和闪光照相的频闪间隔T,求:v0、g、vc
(2)临界问题
典型例题是在排球运动中,为了使从某一位置和某一高度水平扣出的球既不触网、又不出界,扣球速度的取值范围应是多少?
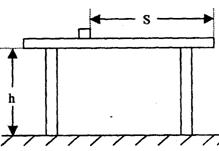
【例2】 已知网高H,半场长L,扣球点高h,扣球点离网水平距离s、求:水平扣球速度v的取值范围。
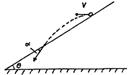
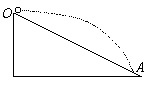 【例3】如图所示,长斜面OA的倾角为θ,放在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中离斜面的最大距离s是多少?
【例3】如图所示,长斜面OA的倾角为θ,放在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中离斜面的最大距离s是多少?
 (3)一个有用的推论
(3)一个有用的推论
平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
 证明:设时间t内物体的水平位移为s,竖直位移为h,则末速度的水平分量vx=v0=s/t,而竖直分量vy=2h/t,
证明:设时间t内物体的水平位移为s,竖直位移为h,则末速度的水平分量vx=v0=s/t,而竖直分量vy=2h/t, ![]() , 所以有
, 所以有![]()
【例4】 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
例题参考答案:
1、解析:水平方向:![]() 竖直方向:
竖直方向:![]()
先求C点的水平分速度vx和竖直分速度vy,再求合速度vC:
![]()
2、解:假设运动员用速度vmax扣球时,球刚好不会出界,用速度vmin扣球时,球刚好不触网,从图中数量关系可得:

![]() ;
;
![]()
实际扣球速度应在这两个值之间。
 3、解析:为计算简便,本题也可不用常规方法来处理,而是将速度和加速度分别沿垂直于斜面和平行于斜面方向进行分解。如图15,速度v0沿垂直斜面方向上的分量为v1=
v0 sinθ,加速度g在垂直于斜面方向上的分量为a=g cosθ,根据分运动各自独立的原理可知,球离斜面的最大距离仅由和决定,当垂直于斜面的分速度减小为零时,球离斜面的距离才是最大。
3、解析:为计算简便,本题也可不用常规方法来处理,而是将速度和加速度分别沿垂直于斜面和平行于斜面方向进行分解。如图15,速度v0沿垂直斜面方向上的分量为v1=
v0 sinθ,加速度g在垂直于斜面方向上的分量为a=g cosθ,根据分运动各自独立的原理可知,球离斜面的最大距离仅由和决定,当垂直于斜面的分速度减小为零时,球离斜面的距离才是最大。![]() 。
。
点评:运动的合成与分解遵守平行四边形定则,有时另辟蹊径可以收到意想不到的效果。
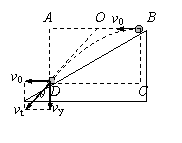
4、解析:以抛出点和落地点连线为对角线画出矩形ABCD,可以证明末速度vt的反向延长线必然交AB于其中点O,由图中可知AD∶AO=2∶![]() ,由相似形可知vt∶v0=
,由相似形可知vt∶v0=![]() ∶
∶![]() ,因此很容易可以得出结论:E /=14J。
,因此很容易可以得出结论:E /=14J。
点评:本题也能用解析法求解。列出竖直分运动和水平分运动的方程,注意到倾角和下落高度和射程的关系,有:h=![]() gt2,s=v0t,
gt2,s=v0t,![]()
或 h=![]() vy t, s=v0 t ,
vy t, s=v0 t ,![]()
同样可求得vt∶v0=![]() ∶
∶![]() ,E /=14J
,E /=14J
针对练习
1.做平抛运动的物体,每秒的速度增量总是
A.大小相等,方向相同; B.大小不等,方向不同
C.大小相等,方向不同 D.大小不等,方向相同
2.从倾角为θ的足够长的斜面上的A点,先后将同一小球以不同的初速度水平向右抛出.第一次初速度为v1,球落到斜面上的瞬时速度方向与斜面夹角为α1,第二次初速度为v2,球落到斜面上的瞬时速度方向与斜面夹角为α2,若v1>v2,则
A.α1>α2 B.α1=α2 C.α1<α2D.无法确定
3.从地面上方同一点向东与西分别平抛出两个等质量的小物体,抛出速度大小分别为v和2v不计空气阻力,则下面关于两个小物体的说法中,正确的是 ( )
A.从抛出到落地动量的增量相同
B.从抛出到落地重力做的功相同
C.从抛出到落地重力的平均功率相同
D.落地时重力的瞬时功率相同
4.如图所示,从倾角为![]() 的斜面上某点先后将同一小球以不同的初速度水平抛出,小球均落在斜面上,当抛出的速度为V1时,小球到达斜面时速度方向与斜面的夹角为
的斜面上某点先后将同一小球以不同的初速度水平抛出,小球均落在斜面上,当抛出的速度为V1时,小球到达斜面时速度方向与斜面的夹角为![]() ;当抛出速度为V2时,小球到达斜面时速度方向与斜面的夹角为
;当抛出速度为V2时,小球到达斜面时速度方向与斜面的夹角为![]() ,则 (
)
,则 (
)
|
B.当V1>V2时,![]() <
<![]()
C.无论V1、V2关系如何,均有![]() =
=![]()
D.![]() 、
、![]() 的关系与斜面倾角
的关系与斜面倾角![]() 有关
有关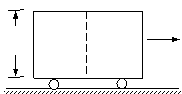
5.如图所示,高为h的车厢在平直轨道上匀减速向右行驶,加速度大小为a ,车厢顶部A点处有油滴滴落到车厢地板上,车厢地板上的O点位于A点的正下方,则油滴落地点必在O点的------------(填左、右)方,离O点距离为-------------------。
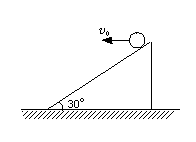 6.如图所示,在倾角为30°的斜面上,沿水平方向抛出一小球,抛出时小球动能为6 J,则小球落回斜面时的动能为_______J.
6.如图所示,在倾角为30°的斜面上,沿水平方向抛出一小球,抛出时小球动能为6 J,则小球落回斜面时的动能为_______J.
7.小球从空中以某一初速度水平抛出,落地前1s时刻,速度方向与水平方向夹30°角,落地时速度方向与水平方向夹60°角,g=10m/s2,求小球在空中运动时间及抛出的初速度。
8.如图所示,飞机离地面高度为H=500m,水平飞行速度为v1=100m/s,追击一辆速度为v2=20 m/s同向行驶的汽车,欲使炸弹击中汽车,飞机应在距离汽车的水平距离多远处投弹?(g=10m/s2)

9.飞机以恒定的速度v沿水平方向飞行,高度为2000m。在飞行过程中释放一枚炸弹,经过30s后飞行员听见炸弹落地的爆炸声。假设此爆炸向空间各个方向的传播速度都为330m/s,炸弹受到的空气阻力可以忽略,求该飞机的飞行速度v?
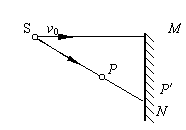 10. 如图所示,点光源S距墙MN的水平距离为L,现从O处以水平速度v0平抛一小球P,P在墙上形成的影是P',在球做平抛运动过程中,其影P'的运动速度是多大?
10. 如图所示,点光源S距墙MN的水平距离为L,现从O处以水平速度v0平抛一小球P,P在墙上形成的影是P',在球做平抛运动过程中,其影P'的运动速度是多大?
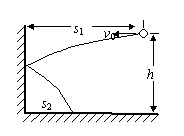 11.在离地面高为h,离竖直光滑墙的水平距离为s1处,有一小球以v0的速度向墙水平抛出,如图所示。小球与墙碰撞后落地,不计碰撞过程中的能量损失,也不考虑碰撞的时间,则落地点到墙的距离s2为多少?
11.在离地面高为h,离竖直光滑墙的水平距离为s1处,有一小球以v0的速度向墙水平抛出,如图所示。小球与墙碰撞后落地,不计碰撞过程中的能量损失,也不考虑碰撞的时间,则落地点到墙的距离s2为多少?
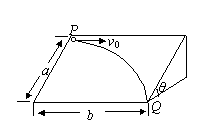 12.如图所示,光滑斜面长为a,宽为b,倾角为θ。一物块沿斜面上方顶点P水平射入,而从右下方顶点Q离开斜面,求物块入射的初速度为多少?
12.如图所示,光滑斜面长为a,宽为b,倾角为θ。一物块沿斜面上方顶点P水平射入,而从右下方顶点Q离开斜面,求物块入射的初速度为多少?
13、如图所示,一小球自平台上水平抛出,恰好落在临近平台的一倾角为 α = 53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8m,g = 10m/s2,sin53° = 0.8,cos53° = 0.6,则
 ⑴小球水平抛出的初速度v0是多少?
⑴小球水平抛出的初速度v0是多少?
⑵斜面顶端与平台边缘的水平距离s是多少?
⑶若斜面顶端高H = 20.8m,则小球离开平台后经多长时间t到达斜面底端?
14、(16分)如图所示,有一质量m=0.05Kg的小滑块静止在高度为h=1.25m的水平桌面上,小滑块到桌子右边缘的距离S=1.0m,小滑块与桌面间的动摩擦因数
![]() ,重力加速度g=10m/s2。现给小滑块V0=4.0m/s的初速度,
,重力加速度g=10m/s2。现给小滑块V0=4.0m/s的初速度,
使滑块沿水平桌面向右滑动。不计空气阻力。求:
|
(2)小滑块经多长时间落地。
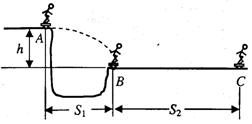
15. (05上海)某滑板爱好者在离地h=1.8m高的平台上滑行,水平离开A点后落在水平地面的B点,其水平位移S1=3m,着地时由于存在能量损失,着地后速度变为v=4m/s,并以此为初速沿水平地面滑行S2=8m后停止.已知人与滑板的总质量m=60kg.求
(1)人与滑板在水平地面滑行时受到的平均阻力大小;
(2)人与滑板离开平台时的水平初速度.(空气阻力忽略不计,g=10m/s2)
参考答案:
1.A 2.B 3、ABCD;4、C; 5、右 ![]() ;6、14
;6、14
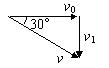 7.解析:设小球的初速度为v0,落地前1s时刻其竖直分速度为v1,由图1知:v1=v0tan300,落地时其竖直分速度为v2,同理v2=v0tan600,v2- v1= g△t,
7.解析:设小球的初速度为v0,落地前1s时刻其竖直分速度为v1,由图1知:v1=v0tan300,落地时其竖直分速度为v2,同理v2=v0tan600,v2- v1= g△t,![]() ,
,![]() ,所以t=1.5s。
,所以t=1.5s。
点评:在解这类基本题型时,需要注意的是:速度、加速度、位移都是矢量,运算时遵守平行四边形定则。
8.解析:炸弹作平抛运动,其下落的时间取决于竖直高度,由![]() 得:
得:![]() s,设距汽车水平距离为s处飞机投弹,则有:
s,设距汽车水平距离为s处飞机投弹,则有:![]() m。
m。
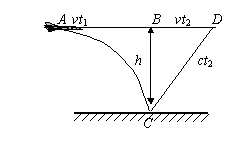 点评:物体作平抛运动飞行的时间只与抛出点和落地点的高度差有关,与物体的质量及初速度无关。先确定运动所需时间有助于问题的解决。
点评:物体作平抛运动飞行的时间只与抛出点和落地点的高度差有关,与物体的质量及初速度无关。先确定运动所需时间有助于问题的解决。
9.解析:设释放炸弹后,炸弹经t1时间落地爆炸,则由平抛运动公式得: ![]() ,设从炸弹爆炸到飞行员听见爆炸声所经过的时间为t2,则由题给条件得t= t1+ t2,由图直角三角形的几何关系可得
,设从炸弹爆炸到飞行员听见爆炸声所经过的时间为t2,则由题给条件得t= t1+ t2,由图直角三角形的几何关系可得![]() ,解得v=262m/s。
,解得v=262m/s。
 点评:根据题中描述的物理情景,画出相应的示意图,充分利用几何关系是处理平抛运动相关问题通常采用的方法。
点评:根据题中描述的物理情景,画出相应的示意图,充分利用几何关系是处理平抛运动相关问题通常采用的方法。
10.解析:设小球经过一段时间运动到某一位置时的水平位移为x,竖直位移为y,对应的影的长度为h,由图知:![]() ,而x= v0 t ,y=
,而x= v0 t ,y=![]() g t2;所以
g t2;所以![]() ,由此看出影子的运动是匀速直线运动,其速度为
,由此看出影子的运动是匀速直线运动,其速度为![]() 。
。
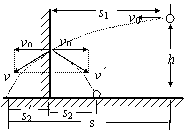 点评:本题将平抛运动与光学有机结合起来,在思考时注意 抓住影子是由于光的直线传播形成的。
点评:本题将平抛运动与光学有机结合起来,在思考时注意 抓住影子是由于光的直线传播形成的。
11.解析:如图所示,小球撞墙的速度v斜向下,其水平分量为v0,由于碰撞无能量损失,故碰撞后小球的速度大小不变,v΄与v关于墙面对称,故v΄的水平分量仍为v0,s2故等于小球没有撞墙时的水平位移s2΄,所以s2=s-s1,s为平抛运动的整个位移,由s= v0
t,![]() 有
有![]() ;
;![]() 。
。
点评:由于碰撞无能量损失,故反弹速度与原速度关于墙面对称,可用平抛运动全程求解是本题的一个亮点。
12.解析:物体在光滑斜面上只受重力和斜面对物体的支持力,因此物体所受到的合力大小为F=![]() ,方向沿斜面向下;根据牛顿第二定律,则物体沿斜面方向的加速度应为a加=
,方向沿斜面向下;根据牛顿第二定律,则物体沿斜面方向的加速度应为a加=![]() ,又由于物体的初速度与a加垂直,所以物体的运动可分解为两个方向的运动,即水平方向是速度为v0的匀速直线运动,沿斜面向下的是初速度为零的匀加速直线运动。因此在水平方向上有 a= v0 t,沿斜面向下的方向上有b=
,又由于物体的初速度与a加垂直,所以物体的运动可分解为两个方向的运动,即水平方向是速度为v0的匀速直线运动,沿斜面向下的是初速度为零的匀加速直线运动。因此在水平方向上有 a= v0 t,沿斜面向下的方向上有b=![]() a加t2;故
a加t2;故![]() 。
。
点评:初速度不为零,加速度恒定且垂直于初速度方向的运动,我们称之为类平抛运动。在解决类平抛运动时,方法完全等同于平抛运动的解法,即将类平抛运动分解为两个相互垂直、且相互独立的分运动,然后按运动的合成与分解的方法去解,本题的创新之处在于解题思维方法的创新,即平抛运动的解题方法推广到类平抛运动中去。
13、解:(1)由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以vy = v0tan53°
vy2 = 2gh
代入数据,得vy = 4m/s,v0 = 3m/s
(2)由vy = gt1得t1 = 0.4s
s =v0t1 = 3×0.4m = 1.2m
(3)小球沿斜面做匀加速直线运动的加速度a =
 初速度 = 5m/s
初速度 = 5m/s
=vt2 + a t22
代入数据,整理得 4t22 + 5t2 - 26 = 0
解得 t2 = 2s 或t2 = - 13s(不合题意舍去)
所以t = t1 + t2 = 2.4s
14、(1)V=![]()
(2)![]()
15、(1)设滑板在水平地面滑行时受到的平均阻力为f,根据动能定理有
![]() ①
①
由①式解得 ![]() ②
②
(2)人和滑板一起在空中做平抛运动,
设初速为v0,飞行时间为t,根据平抛运动规律有
![]() ③
③
![]() ④
④
由③、④两式解得
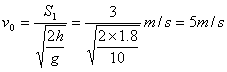 ⑤
⑤