第二轮重点突破(2)——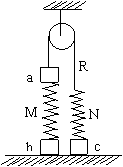弹簧专题

连城一中　林裕光

1.(02广东)图中a、b、c为三个物块，M、N为两个轻质弹簧，R为跨过光滑定滑轮的轻绳，它们连接如图并处于平衡状态。

A.有可能N处于拉伸状态而M处于压缩状态

B.有可能N处于压缩状态而M处于拉伸状态

C.有可能N处于不伸不缩状态而M处于拉伸状态

D.有可能N处于拉伸状态而M处于不伸不缩状态

2．(04吉林理综)如图所示，四个完全相同的弹簧都处于水平位置，它们的右端受到大小皆为F的拉力作用，而左端的情况各不相同：①中弹簧的左端固定在墙上，②中弹簧的左端受大小也为F的拉力作用，③中弹簧的左端拴一小物块，物块在光滑的桌面上滑动，④中弹簧的左端拴一小物块，物块在有摩擦的桌面上滑动。若认为弹簧的质量都为零，以l₁、l₂、l₃、l₄依次表示四个弹簧的伸长量，则有

A．l₂＞l₁　　　 B．l₄＞l₃　　　　C．l₁＞l₃　　　　D．l₂＝l₄

3．如图所示，a、b两根轻弹簧系住一球，球处于静止状态。撤去弹簧a的瞬间，小球的加速度大小为a=2.5m/S²,若弹簧a不动,则撤去弹簧b的瞬间小球加速度可能为：

A. 7.5m/S²,方向竖直向上.　　　　　　　　　　　

B. 7.5m/S²,方向竖直向下.　　　　　　　　  a

C. 12.5m/S²,方向竖直向上.　　　　　　　

D. 12.5m/S²,方向竖直向下.　　　　　　　　 b

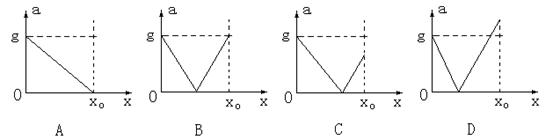
4．如图所示，一根轻弹簧竖直直立在水平地面上，下端固定，在弹簧的正上方有一个物块，物块从高处自由下落到弹簧上端O，将弹簧压缩，弹簧被压缩了x₀时，物块的速度变为零。从物块与弹簧接触开始，物块的加速度的大小随下降的位移x变化的图象，可能是（　　　）

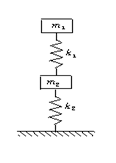5．(99)如图所示，两木块的质量分别为m₁和m₂，两轻质弹簧的劲度系数分别为k₁和k₂，上面木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态。现缓慢向上提上面的木块，直到它刚离开上面弹簧，在这过程中下面木块移动的距离为

A.m₁g/k₁　　　B.m₂g/k₁　　C.m₁g/k₂　　D.m₂g/k₂

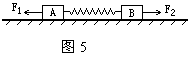6．如图5所示，两物体A、B用轻质弹簧相连静止在光滑水平面上，现同时对A、B两物体施加等大反向的水平恒力F₁、F₂，使A、B同时由静止开始运动，在运动过程中，对A、B两物体及弹簧组成的系统，正确的说法是（整个过程中弹簧不超过其弹性限度）

　　 A.动量始终守恒;

　　 B.机械能始终守恒;

　　 C.当弹簧伸长到最长时，系统的机械能最大;

　D.当弹簧弹力的大小与F₁、F₂的大小相等时，A、B两物速度为零。

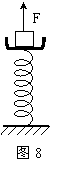
_{7、如图8所示，一个弹簧台秤的秤盘质量和弹簧质量都不计，盘内放一个物体P处于静止，P的质量m=12kg，弹簧的劲度系数k=300N/m。现在给P施加一个竖直向上的力F，使P从静止开始向上做匀加速直线运动，已知在t=0.2s内F是变力，在0.2s以后F是恒力，g=10m/s2,则F的最小值是　　　　  ，F的最大值是　　　　  。}

8．为了测量小木板和斜面的滑动摩擦系数，某同学设计了如下的实验，在小木板上固定一个弹簧秤，（弹簧秤的质量不计），弹簧秤下吊一个光滑的小球。将木板连同小球一起放在斜面上，如图所示，用手固定住木板时，弹簧秤的示数为F₁，放手后木板沿斜面下滑，稳定时弹簧秤的示数为F₂，测的斜面的倾角为q，由测量的数据可以算出小木板跟斜面间的滑动摩擦系数是多少？

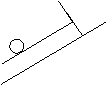
　　　 　　　　　　　　　　　　　　　　　　　　　　 ）q

9、质量为m的物块用压缩的轻质弹簧卡在竖直放置的矩形匣子中，如图14所示，在匣子的顶部和底部都装有压力传感器，当匣子随升降机以a=2．0m／s²的加速度竖直向上做匀减速运动时，匣子项部的压力传感器显示的压力为6．0N，底部的压力传感器显示的压力为10．0N(g=10m／s²)

(1)当匣子顶部压力传感器的示数是底部传感器的示数的一半时，试确定升降机的运动情况。

(2)要使匣子顶部压力传感器的示数为零，升降机沿竖直方向的运动情况可能是怎样的?

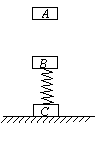10．如图所示，物体B和物体C用劲度系数为k的轻弹簧连接并竖直地静置于水平地面上，此时弹簧的势能为E。这时一个物体A从物体B的正上方由静止释放，下落后与物体B碰撞，碰撞后A与B立刻一起向下运动，但A、B之间并不粘连。已知物体A、B、C的质量均为M，重力加速度为g，忽略空气阻力。求当物体A从距B多大的高度自由落下时，才能使物体C恰好离开水平地面？

11、如图所示，A、B两滑环分别套在间距为1m的光滑细杆上，A和B的质量之比为1:3，用一自然长度为1m的轻弹簧将两环相连，在A环上作用一沿杆方向的、大小为20N的拉力F，当两环都沿杆以相同的加速度运动时，弹簧与杆夹角为53°

（cos53°=0.6）。求弹簧的劲度系数k为多少？

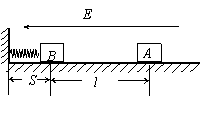12．在绝缘水平面上放一质量m=2.0×10^-3kg的带电滑块A，所带电荷量q=1.0×10^-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B，质量M=4.0×10^-3kg，B与一端连在竖直墙壁上的轻弹簧接触（不连接）且弹簧处于自然状态，弹簧原长S=0.05m.如图所示，在水平面上方空间加一水平向左的匀强电场，电场强度的大小为E=4.0×10⁵N/C，滑块A由静止释放后向左滑动并与滑块B发生碰撞，设碰撞时间极短，碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处（弹性限度内），此时弹性势能E₀=3.2×10^-3J，两滑块始终没有分开，两滑块的体积大小不计，与水平面间的动摩擦因数均为μ=0.5，g取10m/s²。求：

（1）两滑块碰撞后刚结合在一起的共同速度v；

（2）两滑块被弹簧弹开后距竖直墙壁的最大距离s.

13．（8分）如图所示，质量均为m的两个小球A、B套在光滑水平直杆P上，整个直杆被固定于竖直转轴上，并保持水平，两球间用劲度系数为k，自然长度为L的轻质弹簧连接在一起，左边小球被轻质细绳拴在竖直转轴上，细绳长度也为L，现欲使横杆AB随竖直转轴一起在水平面内匀速转动，其角速度为ω，求当弹簧长度稳定后，细绳的拉力和弹簧的总长度为多大？

14．(16分)在纳米技术中需要移动或修补原子，必须使在不停地做热运动(速率约几百米每　　秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间，为此已发明了“激光致冷”技术，若把原子和入射光子分别类比为一辆小车和一个小球，则“激光致冷”与下述的模型很类似。　

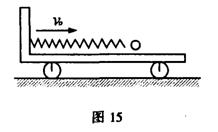
　　一辆质量为m的小车(一侧固定一轻弹簧)，如图15所示，以速度V₀水平向右运动，一动量大小为P，质量可以忽略的小球水平向左射人小车并压缩弹簧至最短，接着被锁定一　　定时间△t，再解除锁定使小球以大小相同的动量P水平向右弹出，紧接着不断重复上述　　过程，最终小车将停下来。设地面和车厢均为光滑，除锁定时间△t外，不计小球在小车上　　运动和弹簧压缩、伸长的时间，求：

　　(1)小球第一次入射后再弹出时，小车的速度的大小和这一过程中小车动能的减少量．

(2)从小球第一次入射开始到小车停止运动所经历的时间．

15．（20分）如图所示，A、B两个矩形木块用轻弹簧相接静止在水

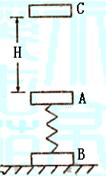
平地面上，弹簧的劲度系数为k，木块A和木块B的质量均为m.

　 （1）若用力将木块A缓慢地竖直向上提起，木块A向上提起多大高

度时，木块B将离开水平地面.

　 （2）若弹簧的劲度系数k是未知的，将一物块C从A的正上方某位

置处无初速释放与A相碰后，立即粘在一起（不再分离）向下运动，它

们到达最低点后又向上运动。已知C的质量为m时，把它从距A高H处

释放，则最终能使B刚好要离开地面。若C的质量为，要使B始终不

离开地面，则释放时，C距A的高度h不能超过多少？

1. A、D　　2．D；3、B D 4、D ；5.C₆ AC _；

_{7分析与解：因为在t=0.2s内F是变力，在t=0.2s以后F是恒力，所以在t=0.2s时，P离开秤盘。此时P受到盘的支持力为零，由于盘和弹簧的质量都不计，所以此时弹簧处于原长。在0_____0.2s这段时间内P向上运动的距离：}

_x=mg/k=0.4m

_{因为，所以P在这段时间的加速度}

_{当P开始运动时拉力最小，此时对物体P有N-mg+Fmin=ma,又因此时N=mg，所以有Fmin=ma=240N.}

_{当P与盘分离时拉力F最大，}

9．(1)当a=2m／s²竖直向下时，由牛顿第二定律，有F_上+rng—F_下=ma

m=0.5kg、 

当匣子顶部板压力传感器的示数是底部传感器的示数的一半时， F_上=F_下=5N

由牛顿第二定律，对m有F_上+mg—2F_下 =ma′　　 a′=0　

所以升降机应作匀速运动

　　(2)若F_上=0,则F_下≥10N,设升降机的加速度为a₁，则：F_上—mg=ma₁

　 a₁=(F_下—mg)／m=(10—5)／0．5=10m／s²，

故升降机作向上的匀加速或向下的匀蛾逮运动，加速度a≥10m／s²．

₁₀解析：设物体A从距B的高度H处自由落下，A与B碰撞前的速度为v₁，由机械能守恒定律得　　　　 v₁=。

设A、B碰撞后共同速度为v₂，则由动量守恒定律得：Mv₁＝2Mv₂，

解得：　　　 v₂＝。

当C刚好离开地面时，由胡克定律得弹簧伸长量为x=Mg/k，由于对称性，所以弹簧的弹性势能仍为E。当弹簧恢复原长时A、B分离，设此时A、B的速度为v₃，则对A、B一起运动的过程中，由机械能守恒得：　，

从A、B分离后到物体C刚好离开地面的过程中，物体B和弹簧组成的系统机械能守恒，即　　　　　　　  。

联立以上方程解得：。

11解：先取A、B和弹簧整体为研究对象，弹簧弹力为内力，杆对A、B支持力与加速度方向垂直，在沿F方向应用牛顿第二定律　　　 F=（m_A+m_B）a　　①2分

　　　 再取B为研究对象，在沿F方向应用牛顿第二定律　　②　2分

　　　 联立①②求解得N

　　　 由几何关系得弹簧的伸长量　　2分

　　　 弹簧的劲度系数　　　　　　　　　　　　　　 2分

　　　 代入数据解得k=100N/m

12解：（1）设两滑块碰前A的速度为v₁，由动能定理有　  

解得：v₁=3m/s

A、B两滑块碰撞，由于时间极短动量守恒，设共同速度为v

  

解得：v=1.0m/s

　（2）碰后A、B一起压缩弹簧至最短，设弹簧压缩量为x₁，由动能定理有：

　　 　　 

解得：x₁=0.02m

设反弹后A、B滑行了x₂距离后速度减为零，由动能定理得：

解得：x₂≈0.05m

以后，因为qE>μ（M+m）g，滑块还会向左运动，但弹开的距离将逐渐变小，所以，最大距离为：S=x₂+s-x₁=0.05m+0.05m-0.02m= 0.08m

13解析：设直杆匀速转动时，弹簧伸长量为x，A、B两球受力分别如图所示，据牛顿第二　定律得：

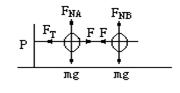对A球有：F_T-F=mω²L………………2分

对B球有：F= mω²(2L+x)-……………………2分

其中F=kx

F_T= mω²L(1+) ,x=……………2分

所以弹簧总长度为

L’=L+x=L……………………2分

14(1)设发生第一次作用后小车的速度为v₁，由动量守恒定律，有

(2)设发生第二次作用后小车的速度为v₂，由动量守恒定律，有

15．（20分）（1）开始时，木块A处于平衡，则kx₁=mg（弹簧压缩）木块B刚好离开地面时，有kx₂=mg（弹簧伸长）

　  故木块A向上提起的高度为x₁+x₂=　 （4分）

　 （2）物块C的质量为m时，它自由下落H高度时的速度v₁=　 ①（2分）

　  设C与A碰撞后的共同速度为v₂，根据动量守恒定律，有mv₁=2mv₂，则v₂=　②（2分）

　 以后A、C继续压缩弹簧，后又向上弹起，最终能使木块B刚好离开地面，此过程中，A、C上升的高度为x₁+x₂=，由于最初弹簧的压缩量x₁与最后的伸长量x₂相等，所以，弹性势能相等，根据机械能守恒定律，有(x₁+x₂)　③（3分）

　  物块C的质量为时，设距A高h处自由下落后刚好能使木块B离开地面，则C下落h高度时的速度　 ④（2分）

　  设C与A碰撞后的共同速度为　 ⑤（2分）

　  A、C碰后果上升高度（x₁+x₂）时，木块B刚好离开地面，此过程中，由机械能守恒定律有(x₁+x₂)　 ⑥（3分）

　  由以上各式消去(x₁+x₂)解得h=H（4分）