第二章　匀变速直线运动的研究（复习学案）

（一）全章知识脉络，知识体系

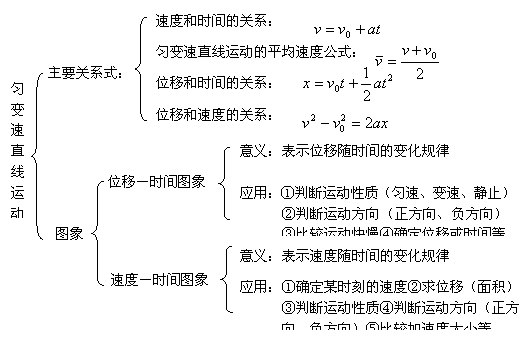（二）知识要点追踪

Ⅰ 匀变速直线运动规律应用

1、匀变速直线运动的规律

实质上是研究做匀变速直线运动物体的初速度v₀、末速度v、加速度a、位移x和时间t这五个量的关系。具体应用时，可以由两个基本公式演绎推理得出几种特殊运动的公式以及各种有用的推论，一般分为如下情况：

（1）从两个基本公式出发，可以解决各种类型的匀变速直线运动的问题。

（2）在分析不知道时间或不需知道时间的问题时，一般用速度位移关系的推论。

（3）处理初速为零的匀加速直线运动和末速为零的匀减速直线运动时，通常用比例关系的方法来解比较方便。

2、匀变速直线运动问题的解题思想

（1）选定研究对象，分析各阶段运动性质；

（2）根据题意画运动草图

（3）根据已知条件及待求量，选定有关规律列出方程，注意抓住加速度a这一关键量；

（4）统一单位制，求解方程。

3、解题方法：

（1）列方程法（2）列不等式法（3）推理分析法（4）图象法

Ⅱ 巧用运动图象解题

运动图象（v-t图象、x-t图象）能直观描述运动规律与特征，我们可以用来定性比较、分析或定量计算、讨论一些物理量。

解题时，要特别重视图象的物理意义，如图象中的截距、斜率、面积、峰值等所代表的物理内涵，这样才能找到解题的突破口。

（三）本章专题剖析

［例1］一物体以初速度v₁做匀变速直线运动，经时间t速度变为v₂求：

（1）物体在时间t内的位移.

（2）物体在中间时刻和中间位置的速度.

（3）比较v_t/2和v_x/2的大小.

［例2］特快列车甲以速率v₁行驶，司机突然发现在正前方距甲车s处有列车乙正以速率v₂（v₂＜v₁）向同一方向运动.为使甲、乙两车不相撞，司机立即使甲车以加速度a做匀减速运动，而乙车仍做原来的匀速运动.求a的大小应满足的条件.

［例3］一船夫驾船沿河道逆水航行，起航时不慎将心爱的酒葫芦落于水中，被水冲走，发现时已航行半小时.船夫马上调转船头去追，问船夫追上酒葫芦尚需多少时间?

［例4］跳伞运动员做低空跳伞表演，他在离地面224 m高处，由静止开始在竖直方向做自由落体运动.一段时间后，立即打开降落伞，以12.5 m/s²的平均加速度匀减速下降，为了运动员的安全，要求运动员落地速度最大不得超过5 m/s（g取10 m/s²）.

（1）求运动员展开伞时，离地面高度至少为多少?着地时相当于从多高处自由落下?

（2）求运动员在空中的最短时间是多少?

（三）课堂练习

1.几个做匀变速直线运动的物体，在t s内位移最大的是

A.加速度最大的物体　　　　　　　  　　　　　　　　　B.初速度最大的物体

C.末速度最大的物体　　　　　　　  　　　　　　　　　D.平均速度最大的物体

2.若某物体做初速度为零的匀加速直线运动，则

A.第4 s内的平均速度大于4 s内的平均速度

B.4 s内的平均速度等于2 s末的瞬时速度

C.第4 s内的速度变化量大于第3 s内的速度变化量

D.第4 s内与前4 s内的位移之比是7∶16

3.一物体由静止沿光滑斜面匀加速下滑距离为l时，速度为v，当它的速度是v/2时，它沿斜面下滑的距离是

A.l/2　　　　  　　B.l　　　　　　  C.l　　　 　　　　　　　　　　 D.l

4.A、B、C三点在同一直线上，某物体自A点从静止开始做匀加速直线运动，经过B点的速度为v.到C点的速度为2v,则AB与BC两段距离大小之比是

A.1∶4　　　　　　　　　　  　　　　　　　　　　　　　　B.1∶3

C.1∶2　　　　　　　　　　  　　　　　　　　　　　　　　D.1∶1

5.一辆汽车做匀速直线运动，在5 s内通过相距50 m的A、B两根电线杆，若汽车经过B杆后改做匀加速直线运动，到达下一根电线杆时速度达到15 m/s，若B、C两杆相距也是 50 m，则此汽车的加速度是______ m/s².

6.物体做匀变速直线运动，它的初速度是1 m/s，在第1 s内的平均速度是15 m/s，它在第6 s内的平均速度是______ m/s.

7.一物体做匀变速直线运动，在第3 s内的位移是15 m,第8 s内的位移是5 m,则物体的初速度为______,加速度为______.

8.一滑块由静止从斜面顶端匀加速下滑，第5 s末的速度是6 m/s，求：

（1）第4 s末的速度；

（2）前7 s内的位移；

（3）第3 s内的位移.